KAN-Papers

Kolmogorov-Arnold Network Papers

A complete list of papers on KANs. Papers with submission dates before the original KAN papers are excluded. You might find this awesome list useful as well. You can find the papers and their titles, abstracts, authors, links, and dates stored in this csv file.

Papers by Month

Number of papers submitted to arXiv by month.

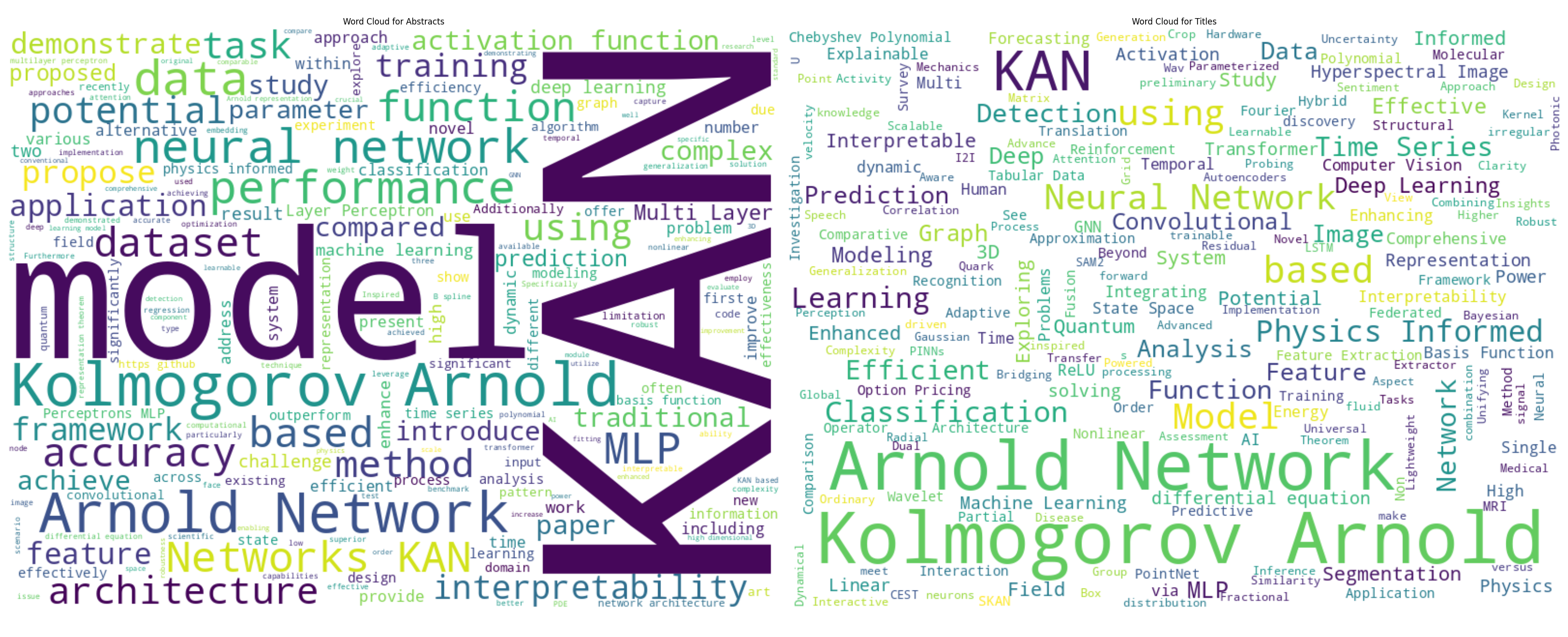
Word Clouds

Word clouds of KAN paper titles and abstracts.

Notebook

You can play with the notebook:

2024

April

KAN: Kolmogorov-Arnold Networks

Authors: Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljačić, Thomas Y. Hou, Max Tegmark

Venue: International Conference on Learning Representations

Citation Count: 534

Abstract: Inspired by the Kolmogorov-Arnold representation theorem, we propose Kolmogorov-Arnold Networks (KANs) as promising alternatives to Multi-Layer Perceptrons (MLPs). While MLPs have fixed activation functions on nodes (“neurons”), KANs have learnable activation functions on edges (“weights”). KANs have no linear weights at all – every weight parameter is replaced by a univariate function parametrized as a spline. We show that this seemingly simple change makes KANs outperform MLPs in terms of accuracy and interpretability. For accuracy, much smaller KANs can achieve comparable or better accuracy than much larger MLPs in data fitting and PDE solving. Theoretically and empirically, KANs possess faster neural scaling laws than MLPs. For interpretability, KANs can be intuitively visualized and can easily interact with human users. Through two examples in mathematics and physics, KANs are shown to be useful collaborators helping scientists (re)discover mathematical and physical laws. In summary, KANs are promising alternatives for MLPs, opening opportunities for further improving today’s deep learning models which rely heavily on MLPs.

May

Biology-inspired joint distribution neurons based on Hierarchical Correlation Reconstruction allowing for multidirectional propagation of values and densities

Author: Jarek Duda

Citation Count: 2

Abstract: Recently a million of biological neurons (BNN) has turned out better from modern RL methods in playing Pong~\cite{RL}, reminding they are still qualitatively superior e.g. in learning, flexibility and robustness - suggesting to try to improve current artificial e.g. MLP/KAN for better agreement with biological. There is proposed extension of KAN approach to neurons containing model of local joint distribution: $ρ(\mathbf{x})=\sum_{\mathbf{j}\in B} a_\mathbf{j} f_\mathbf{j}(\mathbf{x})$ for $\mathbf{x} \in [0,1]^d$, adding interpretation and information flow control to KAN, and allowing to gradually add missing 3 basic properties of biological: 1) biological axons propagate in both directions~\cite{axon}, while current artificial are focused on unidirectional propagation - joint distribution neurons can repair by substituting some variables to get conditional values/distributions for the remaining. 2) Animals show risk avoidance~\cite{risk} requiring to process variance, and generally real world rather needs probabilistic models - the proposed can predict and propagate also distributions as vectors of moments: (expected value, variance) or higher. 3) biological neurons require local training, and beside backpropagation, the proposed allows many additional ways, like direct training, through tensor decomposition, or finally local and promising: information bottleneck. Proposed approach is very general, can be also used as extension of softmax in embeddings of e.g. transformer, suggesting interpretation that features are mixed moments of joint density of real-world properties.

Kolmogorov-Arnold Networks are Radial Basis Function Networks

Author: Ziyao Li

Citation Count: 76

Abstract: This short paper is a fast proof-of-concept that the 3-order B-splines used in Kolmogorov-Arnold Networks (KANs) can be well approximated by Gaussian radial basis functions. Doing so leads to FastKAN, a much faster implementation of KAN which is also a radial basis function (RBF) network.

Chebyshev Polynomial-Based Kolmogorov-Arnold Networks: An Efficient Architecture for Nonlinear Function Approximation

Authors: Sidharth SS, Keerthana AR, Gokul R, Anas KP

Citation Count: 85

Abstract: Accurate approximation of complex nonlinear functions is a fundamental challenge across many scientific and engineering domains. Traditional neural network architectures, such as Multi-Layer Perceptrons (MLPs), often struggle to efficiently capture intricate patterns and irregularities present in high-dimensional functions. This paper presents the Chebyshev Kolmogorov-Arnold Network (Chebyshev KAN), a new neural network architecture inspired by the Kolmogorov-Arnold representation theorem, incorporating the powerful approximation capabilities of Chebyshev polynomials. By utilizing learnable functions parametrized by Chebyshev polynomials on the network’s edges, Chebyshev KANs enhance flexibility, efficiency, and interpretability in function approximation tasks. We demonstrate the efficacy of Chebyshev KANs through experiments on digit classification, synthetic function approximation, and fractal function generation, highlighting their superiority over traditional MLPs in terms of parameter efficiency and interpretability. Our comprehensive evaluation, including ablation studies, confirms the potential of Chebyshev KANs to address longstanding challenges in nonlinear function approximation, paving the way for further advancements in various scientific and engineering applications.

TKAN: Temporal Kolmogorov-Arnold Networks

Authors: Remi Genet, Hugo Inzirillo

Venue: Social Science Research Network

Citation Count: 72

Abstract: Recurrent Neural Networks (RNNs) have revolutionized many areas of machine learning, particularly in natural language and data sequence processing. Long Short-Term Memory (LSTM) has demonstrated its ability to capture long-term dependencies in sequential data. Inspired by the Kolmogorov-Arnold Networks (KANs) a promising alternatives to Multi-Layer Perceptrons (MLPs), we proposed a new neural networks architecture inspired by KAN and the LSTM, the Temporal Kolomogorov-Arnold Networks (TKANs). TKANs combined the strenght of both networks, it is composed of Recurring Kolmogorov-Arnold Networks (RKANs) Layers embedding memory management. This innovation enables us to perform multi-step time series forecasting with enhanced accuracy and efficiency. By addressing the limitations of traditional models in handling complex sequential patterns, the TKAN architecture offers significant potential for advancements in fields requiring more than one step ahead forecasting.

Predictive Modeling of Flexible EHD Pumps using Kolmogorov-Arnold Networks

Authors: Yanhong Peng, Yuxin Wang, Fangchao Hu, Miao He, Zebing Mao, Xia Huang, Jun Ding

Venue: Biomimetic Intelligence and Robotics

Citation Count: 54

Abstract: We present a novel approach to predicting the pressure and flow rate of flexible electrohydrodynamic pumps using the Kolmogorov-Arnold Network. Inspired by the Kolmogorov-Arnold representation theorem, KAN replaces fixed activation functions with learnable spline-based activation functions, enabling it to approximate complex nonlinear functions more effectively than traditional models like Multi-Layer Perceptron and Random Forest. We evaluated KAN on a dataset of flexible EHD pump parameters and compared its performance against RF, and MLP models. KAN achieved superior predictive accuracy, with Mean Squared Errors of 12.186 and 0.001 for pressure and flow rate predictions, respectively. The symbolic formulas extracted from KAN provided insights into the nonlinear relationships between input parameters and pump performance. These findings demonstrate that KAN offers exceptional accuracy and interpretability, making it a promising alternative for predictive modeling in electrohydrodynamic pumping.

Kolmogorov-Arnold Networks (KANs) for Time Series Analysis

Authors: Cristian J. Vaca-Rubio, Luis Blanco, Roberto Pereira, Màrius Caus

Citation Count: 102

Abstract: This paper introduces a novel application of Kolmogorov-Arnold Networks (KANs) to time series forecasting, leveraging their adaptive activation functions for enhanced predictive modeling. Inspired by the Kolmogorov-Arnold representation theorem, KANs replace traditional linear weights with spline-parametrized univariate functions, allowing them to learn activation patterns dynamically. We demonstrate that KANs outperforms conventional Multi-Layer Perceptrons (MLPs) in a real-world satellite traffic forecasting task, providing more accurate results with considerably fewer number of learnable parameters. We also provide an ablation study of KAN-specific parameters impact on performance. The proposed approach opens new avenues for adaptive forecasting models, emphasizing the potential of KANs as a powerful tool in predictive analytics.

Smooth Kolmogorov Arnold networks enabling structural knowledge representation

Authors: Moein E. Samadi, Younes Müller, Andreas Schuppert

Citation Count: 18

Abstract: Kolmogorov-Arnold Networks (KANs) offer an efficient and interpretable alternative to traditional multi-layer perceptron (MLP) architectures due to their finite network topology. However, according to the results of Kolmogorov and Vitushkin, the representation of generic smooth functions by KAN implementations using analytic functions constrained to a finite number of cutoff points cannot be exact. Hence, the convergence of KAN throughout the training process may be limited. This paper explores the relevance of smoothness in KANs, proposing that smooth, structurally informed KANs can achieve equivalence to MLPs in specific function classes. By leveraging inherent structural knowledge, KANs may reduce the data required for training and mitigate the risk of generating hallucinated predictions, thereby enhancing model reliability and performance in computational biomedicine.

Wav-KAN: Wavelet Kolmogorov-Arnold Networks

Authors: Zavareh Bozorgasl, Hao Chen

Venue: Social Science Research Network

Citation Count: 109

Abstract: In this paper, we introduce Wav-KAN, an innovative neural network architecture that leverages the Wavelet Kolmogorov-Arnold Networks (Wav-KAN) framework to enhance interpretability and performance. Traditional multilayer perceptrons (MLPs) and even recent advancements like Spl-KAN face challenges related to interpretability, training speed, robustness, computational efficiency, and performance. Wav-KAN addresses these limitations by incorporating wavelet functions into the Kolmogorov-Arnold network structure, enabling the network to capture both high-frequency and low-frequency components of the input data efficiently. Wavelet-based approximations employ orthogonal or semi-orthogonal basis and maintain a balance between accurately representing the underlying data structure and avoiding overfitting to the noise. While continuous wavelet transform (CWT) has a lot of potentials, we also employed discrete wavelet transform (DWT) for multiresolution analysis, which obviated the need for recalculation of the previous steps in finding the details. Analogous to how water conforms to the shape of its container, Wav-KAN adapts to the data structure, resulting in enhanced accuracy, faster training speeds, and increased robustness compared to Spl-KAN and MLPs. Our results highlight the potential of Wav-KAN as a powerful tool for developing interpretable and high-performance neural networks, with applications spanning various fields. This work sets the stage for further exploration and implementation of Wav-KAN in frameworks such as PyTorch and TensorFlow, aiming to make wavelets in KAN as widespread as activation functions like ReLU and sigmoid in universal approximation theory (UAT). The codes to replicate the simulations are available at https://github.com/zavareh1/Wav-KAN.

Endowing Interpretability for Neural Cognitive Diagnosis by Efficient Kolmogorov-Arnold Networks

Authors: Shangshang Yang, Linrui Qin, Xiaoshan Yu

Citation Count: 10

Abstract: In the realm of intelligent education, cognitive diagnosis plays a crucial role in subsequent recommendation tasks attributed to the revealed students’ proficiency in knowledge concepts. Although neural network-based neural cognitive diagnosis models (CDMs) have exhibited significantly better performance than traditional models, neural cognitive diagnosis is criticized for the poor model interpretability due to the multi-layer perception (MLP) employed, even with the monotonicity assumption. Therefore, this paper proposes to empower the interpretability of neural cognitive diagnosis models through efficient kolmogorov-arnold networks (KANs), named KAN2CD, where KANs are designed to enhance interpretability in two manners. Specifically, in the first manner, KANs are directly used to replace the used MLPs in existing neural CDMs; while in the second manner, the student embedding, exercise embedding, and concept embedding are directly processed by several KANs, and then their outputs are further combined and learned in a unified KAN to get final predictions. To overcome the problem of training KANs slowly, we modify the implementation of original KANs to accelerate the training. Experiments on four real-world datasets show that the proposed KA2NCD exhibits better performance than traditional CDMs, and the proposed KA2NCD still has a bit of performance leading even over the existing neural CDMs. More importantly, the learned structures of KANs enable the proposed KA2NCD to hold as good interpretability as traditional CDMs, which is superior to existing neural CDMs. Besides, the training cost of the proposed KA2NCD is competitive to existing models.

A First Look at Kolmogorov-Arnold Networks in Surrogate-assisted Evolutionary Algorithms

Authors: Hao Hao, Xiaoqun Zhang, Bingdong Li, Aimin Zhou

Citation Count: 6

Abstract: Surrogate-assisted Evolutionary Algorithm (SAEA) is an essential method for solving expensive expensive problems. Utilizing surrogate models to substitute the optimization function can significantly reduce reliance on the function evaluations during the search process, thereby lowering the optimization costs. The construction of surrogate models is a critical component in SAEAs, with numerous machine learning algorithms playing a pivotal role in the model-building phase. This paper introduces Kolmogorov-Arnold Networks (KANs) as surrogate models within SAEAs, examining their application and effectiveness. We employ KANs for regression and classification tasks, focusing on the selection of promising solutions during the search process, which consequently reduces the number of expensive function evaluations. Experimental results indicate that KANs demonstrate commendable performance within SAEAs, effectively decreasing the number of function calls and enhancing the optimization efficiency. The relevant code is publicly accessible and can be found in the GitHub repository.

An Innovative Networks in Federated Learning

Authors: Zavareh Bozorgasl, Hao Chen

Citation Count: 2

Abstract: This paper presents the development and application of Wavelet Kolmogorov-Arnold Networks (Wav-KAN) in federated learning. We implemented Wav-KAN \cite{wav-kan} in the clients. Indeed, we have considered both continuous wavelet transform (CWT) and also discrete wavelet transform (DWT) to enable multiresolution capabaility which helps in heteregeneous data distribution across clients. Extensive experiments were conducted on different datasets, demonstrating Wav-KAN’s superior performance in terms of interpretability, computational speed, training and test accuracy. Our federated learning algorithm integrates wavelet-based activation functions, parameterized by weight, scale, and translation, to enhance local and global model performance. Results show significant improvements in computational efficiency, robustness, and accuracy, highlighting the effectiveness of wavelet selection in scalable neural network design.

DeepOKAN: Deep Operator Network Based on Kolmogorov Arnold Networks for Mechanics Problems

Authors: Diab W. Abueidda, Panos Pantidis, Mostafa E. Mobasher

Venue: Computer Methods in Applied Mechanics and Engineering

Citation Count: 63

Abstract: The modern digital engineering design often requires costly repeated simulations for different scenarios. The prediction capability of neural networks (NNs) makes them suitable surrogates for providing design insights. However, only a few NNs can efficiently handle complex engineering scenario predictions. We introduce a new version of the neural operators called DeepOKAN, which utilizes Kolmogorov Arnold networks (KANs) rather than the conventional neural network architectures. Our DeepOKAN uses Gaussian radial basis functions (RBFs) rather than the B-splines. RBFs offer good approximation properties and are typically computationally fast. The KAN architecture, combined with RBFs, allows DeepOKANs to represent better intricate relationships between input parameters and output fields, resulting in more accurate predictions across various mechanics problems. Specifically, we evaluate DeepOKAN’s performance on several mechanics problems, including 1D sinusoidal waves, 2D orthotropic elasticity, and transient Poisson’s problem, consistently achieving lower training losses and more accurate predictions compared to traditional DeepONets. This approach should pave the way for further improving the performance of neural operators.

June

Kolmogorov-Arnold Network for Satellite Image Classification in Remote Sensing

Author: Minjong Cheon

Citation Count: 47

Abstract: In this research, we propose the first approach for integrating the Kolmogorov-Arnold Network (KAN) with various pre-trained Convolutional Neural Network (CNN) models for remote sensing (RS) scene classification tasks using the EuroSAT dataset. Our novel methodology, named KCN, aims to replace traditional Multi-Layer Perceptrons (MLPs) with KAN to enhance classification performance. We employed multiple CNN-based models, including VGG16, MobileNetV2, EfficientNet, ConvNeXt, ResNet101, and Vision Transformer (ViT), and evaluated their performance when paired with KAN. Our experiments demonstrated that KAN achieved high accuracy with fewer training epochs and parameters. Specifically, ConvNeXt paired with KAN showed the best performance, achieving 94% accuracy in the first epoch, which increased to 96% and remained consistent across subsequent epochs. The results indicated that KAN and MLP both achieved similar accuracy, with KAN performing slightly better in later epochs. By utilizing the EuroSAT dataset, we provided a robust testbed to investigate whether KAN is suitable for remote sensing classification tasks. Given that KAN is a novel algorithm, there is substantial capacity for further development and optimization, suggesting that KCN offers a promising alternative for efficient image analysis in the RS field.

Enhancing Graph Collaborative Filtering with FourierKAN Feature Transformation

Authors: Jinfeng Xu, Zheyu Chen, Jinze Li, Shuo Yang, Wei Wang, Xiping Hu, Edith Ngai

Citation Count: 67

Abstract: Graph Collaborative Filtering (GCF) has emerged as a dominant paradigm in modern recommendation systems, excelling at modeling complex user-item interactions and capturing high-order collaborative signals through graph-structured learning. Most existing GCF models predominantly rely on simplified graph architectures like LightGCN, which strategically remove feature transformation and activation functions from vanilla graph convolution networks. Through systematic analysis, we reveal that feature transformation in message propagation can enhance model representation, though at the cost of increased training difficulty. To this end, we propose FourierKAN-GCF, a novel GCN framework that adopts Fourier Kolmogorov-Arnold Networks as efficient transformation modules within graph propagation layers. This design enhances model representation while decreasing training difficulty. Our FourierKAN-GCF can achieve higher recommendation performance than most widely used GCF backbone models. In addition, it can be integrated into existing advanced self-supervised models as a backbone, replacing their original backbone to achieve enhanced performance. Extensive experiments on three public datasets demonstrate the superiority of FourierKAN-GCF.

iKAN: Global Incremental Learning with KAN for Human Activity Recognition Across Heterogeneous Datasets

Authors: Mengxi Liu, Sizhen Bian, Bo Zhou, Paul Lukowicz

Venue: International Workshop on the Semantic Web

Citation Count: 20

Abstract: This work proposes an incremental learning (IL) framework for wearable sensor human activity recognition (HAR) that tackles two challenges simultaneously: catastrophic forgetting and non-uniform inputs. The scalable framework, iKAN, pioneers IL with Kolmogorov-Arnold Networks (KAN) to replace multi-layer perceptrons as the classifier that leverages the local plasticity and global stability of splines. To adapt KAN for HAR, iKAN uses task-specific feature branches and a feature redistribution layer. Unlike existing IL methods that primarily adjust the output dimension or the number of classifier nodes to adapt to new tasks, iKAN focuses on expanding the feature extraction branches to accommodate new inputs from different sensor modalities while maintaining consistent dimensions and the number of classifier outputs. Continual learning across six public HAR datasets demonstrated the iKAN framework’s incremental learning performance, with a last performance of 84.9\% (weighted F1 score) and an average incremental performance of 81.34\%, which significantly outperforms the two existing incremental learning methods, such as EWC (51.42\%) and experience replay (59.92\%).

ReLU-KAN: New Kolmogorov-Arnold Networks that Only Need Matrix Addition, Dot Multiplication, and ReLU

Authors: Qi Qiu, Tao Zhu, Helin Gong, Liming Chen, Huansheng Ning

Citation Count: 25

Abstract: Limited by the complexity of basis function (B-spline) calculations, Kolmogorov-Arnold Networks (KAN) suffer from restricted parallel computing capability on GPUs. This paper proposes a novel ReLU-KAN implementation that inherits the core idea of KAN. By adopting ReLU (Rectified Linear Unit) and point-wise multiplication, we simplify the design of KAN’s basis function and optimize the computation process for efficient CUDA computing. The proposed ReLU-KAN architecture can be readily implemented on existing deep learning frameworks (e.g., PyTorch) for both inference and training. Experimental results demonstrate that ReLU-KAN achieves a 20x speedup compared to traditional KAN with 4-layer networks. Furthermore, ReLU-KAN exhibits a more stable training process with superior fitting ability while preserving the “catastrophic forgetting avoidance” property of KAN. You can get the code in https://github.com/quiqi/relu_kan

A Temporal Kolmogorov-Arnold Transformer for Time Series Forecasting

Authors: Remi Genet, Hugo Inzirillo

Citation Count: 43

Abstract: Capturing complex temporal patterns and relationships within multivariate data streams is a difficult task. We propose the Temporal Kolmogorov-Arnold Transformer (TKAT), a novel attention-based architecture designed to address this task using Temporal Kolmogorov-Arnold Networks (TKANs). Inspired by the Temporal Fusion Transformer (TFT), TKAT emerges as a powerful encoder-decoder model tailored to handle tasks in which the observed part of the features is more important than the a priori known part. This new architecture combined the theoretical foundation of the Kolmogorov-Arnold representation with the power of transformers. TKAT aims to simplify the complex dependencies inherent in time series, making them more “interpretable”. The use of transformer architecture in this framework allows us to capture long-range dependencies through self-attention mechanisms.

Kolmogorov-Arnold Networks for Time Series: Bridging Predictive Power and Interpretability

Authors: Kunpeng Xu, Lifei Chen, Shengrui Wang

Citation Count: 59

Abstract: Kolmogorov-Arnold Networks (KAN) is a groundbreaking model recently proposed by the MIT team, representing a revolutionary approach with the potential to be a game-changer in the field. This innovative concept has rapidly garnered worldwide interest within the AI community. Inspired by the Kolmogorov-Arnold representation theorem, KAN utilizes spline-parametrized univariate functions in place of traditional linear weights, enabling them to dynamically learn activation patterns and significantly enhancing interpretability. In this paper, we explore the application of KAN to time series forecasting and propose two variants: T-KAN and MT-KAN. T-KAN is designed to detect concept drift within time series and can explain the nonlinear relationships between predictions and previous time steps through symbolic regression, making it highly interpretable in dynamically changing environments. MT-KAN, on the other hand, improves predictive performance by effectively uncovering and leveraging the complex relationships among variables in multivariate time series. Experiments validate the effectiveness of these approaches, demonstrating that T-KAN and MT-KAN significantly outperform traditional methods in time series forecasting tasks, not only enhancing predictive accuracy but also improving model interpretability. This research opens new avenues for adaptive forecasting models, highlighting the potential of KAN as a powerful and interpretable tool in predictive analytics.

Exploring the Potential of Polynomial Basis Functions in Kolmogorov-Arnold Networks: A Comparative Study of Different Groups of Polynomials

Author: Seyd Teymoor Seydi

Citation Count: 17

Abstract: This paper presents a comprehensive survey of 18 distinct polynomials and their potential applications in Kolmogorov-Arnold Network (KAN) models as an alternative to traditional spline-based methods. The polynomials are classified into various groups based on their mathematical properties, such as orthogonal polynomials, hypergeometric polynomials, q-polynomials, Fibonacci-related polynomials, combinatorial polynomials, and number-theoretic polynomials. The study aims to investigate the suitability of these polynomials as basis functions in KAN models for complex tasks like handwritten digit classification on the MNIST dataset. The performance metrics of the KAN models, including overall accuracy, Kappa, and F1 score, are evaluated and compared. The Gottlieb-KAN model achieves the highest performance across all metrics, suggesting its potential as a suitable choice for the given task. However, further analysis and tuning of these polynomials on more complex datasets are necessary to fully understand their capabilities in KAN models. The source code for the implementation of these KAN models is available at https://github.com/seydi1370/Basis_Functions .

Leveraging KANs For Enhanced Deep Koopman Operator Discovery

Authors: George Nehma, Madhur Tiwari

Citation Count: 11

Abstract: Multi-layer perceptrons (MLP’s) have been extensively utilized in discovering Deep Koopman operators for linearizing nonlinear dynamics. With the emergence of Kolmogorov-Arnold Networks (KANs) as a more efficient and accurate alternative to the MLP Neural Network, we propose a comparison of the performance of each network type in the context of learning Koopman operators with control. In this work, we propose a KANs-based deep Koopman framework with applications to an orbital Two-Body Problem (2BP) and the pendulum for data-driven discovery of linear system dynamics. KANs were found to be superior in nearly all aspects of training; learning 31 times faster, being 15 times more parameter efficiency, and predicting 1.25 times more accurately as compared to the MLP Deep Neural Networks (DNNs) in the case of the 2BP. Thus, KANs shows potential for being an efficient tool in the development of Deep Koopman Theory.

A comprehensive and FAIR comparison between MLP and KAN representations for differential equations and operator networks

Authors: Khemraj Shukla, Juan Diego Toscano, Zhicheng Wang, Zongren Zou, George Em Karniadakis

Venue: Computer Methods in Applied Mechanics and Engineering

Citation Count: 80

Abstract: Kolmogorov-Arnold Networks (KANs) were recently introduced as an alternative representation model to MLP. Herein, we employ KANs to construct physics-informed machine learning models (PIKANs) and deep operator models (DeepOKANs) for solving differential equations for forward and inverse problems. In particular, we compare them with physics-informed neural networks (PINNs) and deep operator networks (DeepONets), which are based on the standard MLP representation. We find that although the original KANs based on the B-splines parameterization lack accuracy and efficiency, modified versions based on low-order orthogonal polynomials have comparable performance to PINNs and DeepONet although they still lack robustness as they may diverge for different random seeds or higher order orthogonal polynomials. We visualize their corresponding loss landscapes and analyze their learning dynamics using information bottleneck theory. Our study follows the FAIR principles so that other researchers can use our benchmarks to further advance this emerging topic.

U-KAN Makes Strong Backbone for Medical Image Segmentation and Generation

Authors: Chenxin Li, Xinyu Liu, Wuyang Li, Cheng Wang, Hengyu Liu, Yifan Liu, Zhen Chen, Yixuan Yuan

Venue: AAAI Conference on Artificial Intelligence

Citation Count: 130

Abstract: U-Net has become a cornerstone in various visual applications such as image segmentation and diffusion probability models. While numerous innovative designs and improvements have been introduced by incorporating transformers or MLPs, the networks are still limited to linearly modeling patterns as well as the deficient interpretability. To address these challenges, our intuition is inspired by the impressive results of the Kolmogorov-Arnold Networks (KANs) in terms of accuracy and interpretability, which reshape the neural network learning via the stack of non-linear learnable activation functions derived from the Kolmogorov-Anold representation theorem. Specifically, in this paper, we explore the untapped potential of KANs in improving backbones for vision tasks. We investigate, modify and re-design the established U-Net pipeline by integrating the dedicated KAN layers on the tokenized intermediate representation, termed U-KAN. Rigorous medical image segmentation benchmarks verify the superiority of U-KAN by higher accuracy even with less computation cost. We further delved into the potential of U-KAN as an alternative U-Net noise predictor in diffusion models, demonstrating its applicability in generating task-oriented model architectures. These endeavours unveil valuable insights and sheds light on the prospect that with U-KAN, you can make strong backbone for medical image segmentation and generation. Project page:\url{https://yes-u-kan.github.io/}.

GKAN: Graph Kolmogorov-Arnold Networks

Authors: Mehrdad Kiamari, Mohammad Kiamari, Bhaskar Krishnamachari

Citation Count: 42

Abstract: We introduce Graph Kolmogorov-Arnold Networks (GKAN), an innovative neural network architecture that extends the principles of the recently proposed Kolmogorov-Arnold Networks (KAN) to graph-structured data. By adopting the unique characteristics of KANs, notably the use of learnable univariate functions instead of fixed linear weights, we develop a powerful model for graph-based learning tasks. Unlike traditional Graph Convolutional Networks (GCNs) that rely on a fixed convolutional architecture, GKANs implement learnable spline-based functions between layers, transforming the way information is processed across the graph structure. We present two different ways to incorporate KAN layers into GKAN: architecture 1 – where the learnable functions are applied to input features after aggregation and architecture 2 – where the learnable functions are applied to input features before aggregation. We evaluate GKAN empirically using a semi-supervised graph learning task on a real-world dataset (Cora). We find that architecture generally performs better. We find that GKANs achieve higher accuracy in semi-supervised learning tasks on graphs compared to the traditional GCN model. For example, when considering 100 features, GCN provides an accuracy of 53.5 while a GKAN with a comparable number of parameters gives an accuracy of 61.76; with 200 features, GCN provides an accuracy of 61.24 while a GKAN with a comparable number of parameters gives an accuracy of 67.66. We also present results on the impact of various parameters such as the number of hidden nodes, grid-size, and the polynomial-degree of the spline on the performance of GKAN.

fKAN: Fractional Kolmogorov-Arnold Networks with trainable Jacobi basis functions

Author: Alireza Afzal Aghaei

Venue: Neurocomputing

Citation Count: 50

Abstract: Recent advancements in neural network design have given rise to the development of Kolmogorov-Arnold Networks (KANs), which enhance speed, interpretability, and precision. This paper presents the Fractional Kolmogorov-Arnold Network (fKAN), a novel neural network architecture that incorporates the distinctive attributes of KANs with a trainable adaptive fractional-orthogonal Jacobi function as its basis function. By leveraging the unique mathematical properties of fractional Jacobi functions, including simple derivative formulas, non-polynomial behavior, and activity for both positive and negative input values, this approach ensures efficient learning and enhanced accuracy. The proposed architecture is evaluated across a range of tasks in deep learning and physics-informed deep learning. Precision is tested on synthetic regression data, image classification, image denoising, and sentiment analysis. Additionally, the performance is measured on various differential equations, including ordinary, partial, and fractional delay differential equations. The results demonstrate that integrating fractional Jacobi functions into KANs significantly improves training speed and performance across diverse fields and applications.

Unveiling the Power of Wavelets: A Wavelet-based Kolmogorov-Arnold Network for Hyperspectral Image Classification

Authors: Seyd Teymoor Seydi, Zavareh Bozorgasl, Hao Chen

Citation Count: 27

Abstract: Hyperspectral image classification is a crucial but challenging task due to the high dimensionality and complex spatial-spectral correlations inherent in hyperspectral data. This paper employs Wavelet-based Kolmogorov-Arnold Network (wav-kan) architecture tailored for efficient modeling of these intricate dependencies. Inspired by the Kolmogorov-Arnold representation theorem, Wav-KAN incorporates wavelet functions as learnable activation functions, enabling non-linear mapping of the input spectral signatures. The wavelet-based activation allows Wav-KAN to effectively capture multi-scale spatial and spectral patterns through dilations and translations. Experimental evaluation on three benchmark hyperspectral datasets (Salinas, Pavia, Indian Pines) demonstrates the superior performance of Wav-KAN compared to traditional multilayer perceptrons (MLPs) and the recently proposed Spline-based KAN (Spline-KAN) model. In this work we are: (1) conducting more experiments on additional hyperspectral datasets (Pavia University, WHU-Hi, and Urban Hyperspectral Image) to further validate the generalizability of Wav-KAN; (2) developing a multiresolution Wav-KAN architecture to capture scale-invariant features; (3) analyzing the effect of dimensional reduction techniques on classification performance; (4) exploring optimization methods for tuning the hyperparameters of KAN models; and (5) comparing Wav-KAN with other state-of-the-art models in hyperspectral image classification.

Suitability of KANs for Computer Vision: A preliminary investigation

Authors: Basim Azam, Naveed Akhtar

Citation Count: 30

Abstract: Kolmogorov-Arnold Networks (KANs) introduce a paradigm of neural modeling that implements learnable functions on the edges of the networks, diverging from the traditional node-centric activations in neural networks. This work assesses the applicability and efficacy of KANs in visual modeling, focusing on fundamental recognition and segmentation tasks. We mainly analyze the performance and efficiency of different network architectures built using KAN concepts along with conventional building blocks of convolutional and linear layers, enabling a comparative analysis with the conventional models. Our findings are aimed at contributing to understanding the potential of KANs in computer vision, highlighting both their strengths and areas for further research. Our evaluation point toward the fact that while KAN-based architectures perform in line with the original claims, it may often be important to employ more complex functions on the network edges to retain the performance advantage of KANs on more complex visual data.

SCKansformer: Fine-Grained Classification of Bone Marrow Cells via Kansformer Backbone and Hierarchical Attention Mechanisms

Authors: Yifei Chen, Zhu Zhu, Shenghao Zhu, Linwei Qiu, Binfeng Zou, Fan Jia, Yunpeng Zhu, Chenyan Zhang, Zhaojie Fang, Feiwei Qin, Jin Fan, Changmiao Wang, Yu Gao, Gang Yu

Abstract: The incidence and mortality rates of malignant tumors, such as acute leukemia, have risen significantly. Clinically, hospitals rely on cytological examination of peripheral blood and bone marrow smears to diagnose malignant tumors, with accurate blood cell counting being crucial. Existing automated methods face challenges such as low feature expression capability, poor interpretability, and redundant feature extraction when processing high-dimensional microimage data. We propose a novel fine-grained classification model, SCKansformer, for bone marrow blood cells, which addresses these challenges and enhances classification accuracy and efficiency. The model integrates the Kansformer Encoder, SCConv Encoder, and Global-Local Attention Encoder. The Kansformer Encoder replaces the traditional MLP layer with the KAN, improving nonlinear feature representation and interpretability. The SCConv Encoder, with its Spatial and Channel Reconstruction Units, enhances feature representation and reduces redundancy. The Global-Local Attention Encoder combines Multi-head Self-Attention with a Local Part module to capture both global and local features. We validated our model using the Bone Marrow Blood Cell Fine-Grained Classification Dataset (BMCD-FGCD), comprising over 10,000 samples and nearly 40 classifications, developed with a partner hospital. Comparative experiments on our private dataset, as well as the publicly available PBC and ALL-IDB datasets, demonstrate that SCKansformer outperforms both typical and advanced microcell classification methods across all datasets. Our source code and private BMCD-FGCD dataset are available at https://github.com/JustlfC03/SCKansformer.

Kolmogorov Arnold Informed neural network: A physics-informed deep learning framework for solving forward and inverse problems based on Kolmogorov Arnold Networks

Authors: Yizheng Wang, Jia Sun, Jinshuai Bai, Cosmin Anitescu, Mohammad Sadegh Eshaghi, Xiaoying Zhuang, Timon Rabczuk, Yinghua Liu

Venue: Computer Methods in Applied Mechanics and Engineering

Citation Count: 39

Abstract: AI for partial differential equations (PDEs) has garnered significant attention, particularly with the emergence of Physics-informed neural networks (PINNs). The recent advent of Kolmogorov-Arnold Network (KAN) indicates that there is potential to revisit and enhance the previously MLP-based PINNs. Compared to MLPs, KANs offer interpretability and require fewer parameters. PDEs can be described in various forms, such as strong form, energy form, and inverse form. While mathematically equivalent, these forms are not computationally equivalent, making the exploration of different PDE formulations significant in computational physics. Thus, we propose different PDE forms based on KAN instead of MLP, termed Kolmogorov-Arnold-Informed Neural Network (KINN) for solving forward and inverse problems. We systematically compare MLP and KAN in various numerical examples of PDEs, including multi-scale, singularity, stress concentration, nonlinear hyperelasticity, heterogeneous, and complex geometry problems. Our results demonstrate that KINN significantly outperforms MLP regarding accuracy and convergence speed for numerous PDEs in computational solid mechanics, except for the complex geometry problem. This highlights KINN’s potential for more efficient and accurate PDE solutions in AI for PDEs.

BSRBF-KAN: A combination of B-splines and Radial Basis Functions in Kolmogorov-Arnold Networks

Author: Hoang-Thang Ta

Citation Count: 30

Abstract: In this paper, we introduce BSRBF-KAN, a Kolmogorov Arnold Network (KAN) that combines B-splines and radial basis functions (RBFs) to fit input vectors during data training. We perform experiments with BSRBF-KAN, multi-layer perception (MLP), and other popular KANs, including EfficientKAN, FastKAN, FasterKAN, and GottliebKAN over the MNIST and Fashion-MNIST datasets. BSRBF-KAN shows stability in 5 training runs with a competitive average accuracy of 97.55% on MNIST and 89.33% on Fashion-MNIST and obtains convergence better than other networks. We expect BSRBF-KAN to open many combinations of mathematical functions to design KANs. Our repo is publicly available at: https://github.com/hoangthangta/BSRBF_KAN.

Realizability-Informed Machine Learning for Turbulence Anisotropy Mappings

Authors: Ryley McConkey, Nikhila Kalia, Eugene Yee, Fue-Sang Lien

Citation Count: 1

Abstract: Within the context of machine learning-based closure mappings for RANS turbulence modelling, physical realizability is often enforced using ad-hoc postprocessing of the predicted anisotropy tensor. In this study, we address the realizability issue via a new physics-based loss function that penalizes non-realizable results during training, thereby embedding a preference for realizable predictions into the model. Additionally, we propose a new framework for data-driven turbulence modelling which retains the stability and conditioning of optimal eddy viscosity-based approaches while embedding equivariance. Several modifications to the tensor basis neural network to enhance training and testing stability are proposed. We demonstrate the conditioning, stability, and generalization of the new framework and model architecture on three flows: flow over a flat plate, flow over periodic hills, and flow through a square duct. The realizability-informed loss function is demonstrated to significantly increase the number of realizable predictions made by the model when generalizing to a new flow configuration. Altogether, the proposed framework enables the training of stable and equivariant anisotropy mappings, with more physically realizable predictions on new data. We make our code available for use and modification by others. Moreover, as part of this study, we explore the applicability of Kolmogorov-Arnold Networks (KAN) to turbulence modeling, assessing its potential to address non-linear mappings in the anisotropy tensor predictions and demonstrating promising results for the flat plate case.

Initial Investigation of Kolmogorov-Arnold Networks (KANs) as Feature Extractors for IMU Based Human Activity Recognition

Authors: Mengxi Liu, Daniel Geißler, Dominique Nshimyimana, Sizhen Bian, Bo Zhou, Paul Lukowicz

Venue: Companion of the 2024 on ACM International Joint Conference on Pervasive and Ubiquitous Computing

Citation Count: 11

Abstract: In this work, we explore the use of a novel neural network architecture, the Kolmogorov-Arnold Networks (KANs) as feature extractors for sensor-based (specifically IMU) Human Activity Recognition (HAR). Where conventional networks perform a parameterized weighted sum of the inputs at each node and then feed the result into a statically defined nonlinearity, KANs perform non-linear computations represented by B-SPLINES on the edges leading to each node and then just sum up the inputs at the node. Instead of learning weights, the system learns the spline parameters. In the original work, such networks have been shown to be able to more efficiently and exactly learn sophisticated real valued functions e.g. in regression or PDE solution. We hypothesize that such an ability is also advantageous for computing low-level features for IMU-based HAR. To this end, we have implemented KAN as the feature extraction architecture for IMU-based human activity recognition tasks, including four architecture variations. We present an initial performance investigation of the KAN feature extractor on four public HAR datasets. It shows that the KAN-based feature extractor outperforms CNN-based extractors on all datasets while being more parameter efficient.

Convolutional Kolmogorov-Arnold Networks

Authors: Alexander Dylan Bodner, Antonio Santiago Tepsich, Jack Natan Spolski, Santiago Pourteau

Citation Count: 68

Abstract: In this paper, we present Convolutional Kolmogorov-Arnold Networks, a novel architecture that integrates the learnable spline-based activation functions of Kolmogorov-Arnold Networks (KANs) into convolutional layers. By replacing traditional fixed-weight kernels with learnable non-linear functions, Convolutional KANs offer a significant improvement in parameter efficiency and expressive power over standard Convolutional Neural Networks (CNNs). We empirically evaluate Convolutional KANs on the Fashion-MNIST dataset, demonstrating competitive accuracy with up to 50% fewer parameters compared to baseline classic convolutions. This suggests that the KAN Convolution can effectively capture complex spatial relationships with fewer resources, offering a promising alternative for parameter-efficient deep learning models.

GraphKAN: Enhancing Feature Extraction with Graph Kolmogorov Arnold Networks

Authors: Fan Zhang, Xin Zhang

Citation Count: 29

Abstract: Massive number of applications involve data with underlying relationships embedded in non-Euclidean space. Graph neural networks (GNNs) are utilized to extract features by capturing the dependencies within graphs. Despite groundbreaking performances, we argue that Multi-layer perceptrons (MLPs) and fixed activation functions impede the feature extraction due to information loss. Inspired by Kolmogorov Arnold Networks (KANs), we make the first attempt to GNNs with KANs. We discard MLPs and activation functions, and instead used KANs for feature extraction. Experiments demonstrate the effectiveness of GraphKAN, emphasizing the potential of KANs as a powerful tool. Code is available at https://github.com/Ryanfzhang/GraphKan.

rKAN: Rational Kolmogorov-Arnold Networks

Author: Alireza Afzal Aghaei

Citation Count: 19

Abstract: The development of Kolmogorov-Arnold networks (KANs) marks a significant shift from traditional multi-layer perceptrons in deep learning. Initially, KANs employed B-spline curves as their primary basis function, but their inherent complexity posed implementation challenges. Consequently, researchers have explored alternative basis functions such as Wavelets, Polynomials, and Fractional functions. In this research, we explore the use of rational functions as a novel basis function for KANs. We propose two different approaches based on Pade approximation and rational Jacobi functions as trainable basis functions, establishing the rational KAN (rKAN). We then evaluate rKAN’s performance in various deep learning and physics-informed tasks to demonstrate its practicality and effectiveness in function approximation.

A Benchmarking Study of Kolmogorov-Arnold Networks on Tabular Data

Authors: Eleonora Poeta, Flavio Giobergia, Eliana Pastor, Tania Cerquitelli, Elena Baralis

Venue: Advanced Industrial Conference on Telecommunications

Citation Count: 21

Abstract: Kolmogorov-Arnold Networks (KANs) have very recently been introduced into the world of machine learning, quickly capturing the attention of the entire community. However, KANs have mostly been tested for approximating complex functions or processing synthetic data, while a test on real-world tabular datasets is currently lacking. In this paper, we present a benchmarking study comparing KANs and Multi-Layer Perceptrons (MLPs) on tabular datasets. The study evaluates task performance and training times. From the results obtained on the various datasets, KANs demonstrate superior or comparable accuracy and F1 scores, excelling particularly in datasets with numerous instances, suggesting robust handling of complex data. We also highlight that this performance improvement of KANs comes with a higher computational cost when compared to MLPs of comparable sizes.

Demonstrating the Efficacy of Kolmogorov-Arnold Networks in Vision Tasks

Author: Minjong Cheon

Citation Count: 39

Abstract: In the realm of deep learning, the Kolmogorov-Arnold Network (KAN) has emerged as a potential alternative to multilayer projections (MLPs). However, its applicability to vision tasks has not been extensively validated. In our study, we demonstrated the effectiveness of KAN for vision tasks through multiple trials on the MNIST, CIFAR10, and CIFAR100 datasets, using a training batch size of 32. Our results showed that while KAN outperformed the original MLP-Mixer on CIFAR10 and CIFAR100, it performed slightly worse than the state-of-the-art ResNet-18. These findings suggest that KAN holds significant promise for vision tasks, and further modifications could enhance its performance in future evaluations.Our contributions are threefold: first, we showcase the efficiency of KAN-based algorithms for visual tasks; second, we provide extensive empirical assessments across various vision benchmarks, comparing KAN’s performance with MLP-Mixer, CNNs, and Vision Transformers (ViT); and third, we pioneer the use of natural KAN layers in visual tasks, addressing a gap in previous research. This paper lays the foundation for future studies on KANs, highlighting their potential as a reliable alternative for image classification tasks.

How to Learn More? Exploring Kolmogorov-Arnold Networks for Hyperspectral Image Classification

Authors: Ali Jamali, Swalpa Kumar Roy, Danfeng Hong, Bing Lu, Pedram Ghamisi

Venue: Remote Sensing

Citation Count: 28

Abstract: Convolutional Neural Networks (CNNs) and vision transformers (ViTs) have shown excellent capability in complex hyperspectral image (HSI) classification. However, these models require a significant number of training data and are computational resources. On the other hand, modern Multi-Layer Perceptrons (MLPs) have demonstrated great classification capability. These modern MLP-based models require significantly less training data compared to CNNs and ViTs, achieving the state-of-the-art classification accuracy. Recently, Kolmogorov-Arnold Networks (KANs) were proposed as viable alternatives for MLPs. Because of their internal similarity to splines and their external similarity to MLPs, KANs are able to optimize learned features with remarkable accuracy in addition to being able to learn new features. Thus, in this study, we assess the effectiveness of KANs for complex HSI data classification. Moreover, to enhance the HSI classification accuracy obtained by the KANs, we develop and propose a Hybrid architecture utilizing 1D, 2D, and 3D KANs. To demonstrate the effectiveness of the proposed KAN architecture, we conducted extensive experiments on three newly created HSI benchmark datasets: QUH-Pingan, QUH-Tangdaowan, and QUH-Qingyun. The results underscored the competitive or better capability of the developed hybrid KAN-based model across these benchmark datasets over several other CNN- and ViT-based algorithms, including 1D-CNN, 2DCNN, 3D CNN, VGG-16, ResNet-50, EfficientNet, RNN, and ViT. The code are publicly available at (https://github.com/aj1365/HSIConvKAN)

CEST-KAN: Kolmogorov-Arnold Networks for CEST MRI Data Analysis

Authors: Jiawen Wang, Pei Cai, Ziyan Wang, Huabin Zhang, Jianpan Huang

Citation Count: 7

Abstract: Purpose: This study aims to propose and investigate the feasibility of using Kolmogorov-Arnold Network (KAN) for CEST MRI data analysis (CEST-KAN). Methods: CEST MRI data were acquired from twelve healthy volunteers at 3T. Data from ten subjects were used for training, while the remaining two were reserved for testing. The performance of multi-layer perceptron (MLP) and KAN models with the same network settings were evaluated and compared to the conventional multi-pool Lorentzian fitting (MPLF) method in generating water and multiple CEST contrasts, including amide, relayed nuclear Overhauser effect (rNOE), and magnetization transfer (MT). Results: The water and CEST maps generated by both MLP and KAN were visually comparable to the MPLF results. However, the KAN model demonstrated higher accuracy in extrapolating the CEST fitting metrics, as evidenced by the smaller validation loss during training and smaller absolute error during testing. Voxel-wise correlation analysis showed that all four CEST fitting metrics generated by KAN consistently exhibited higher Pearson coefficients than the MLP results, indicating superior performance. Moreover, the KAN models consistently outperformed the MLP models in varying hidden layer numbers despite longer training time. Conclusion: In this study, we demonstrated for the first time the feasibility of utilizing KAN for CEST MRI data analysis, highlighting its superiority over MLP in this task. The findings suggest that CEST-KAN has the potential to be a robust and reliable post-analysis tool for CEST MRI in clinical settings.

KANQAS: Kolmogorov-Arnold Network for Quantum Architecture Search

Authors: Akash Kundu, Aritra Sarkar, Abhishek Sadhu

Venue: EPJ Quantum Technology

Citation Count: 31

Abstract: Quantum architecture Search (QAS) is a promising direction for optimization and automated design of quantum circuits towards quantum advantage. Recent techniques in QAS emphasize Multi-Layer Perceptron (MLP)-based deep Q-networks. However, their interpretability remains challenging due to the large number of learnable parameters and the complexities involved in selecting appropriate activation functions. In this work, to overcome these challenges, we utilize the Kolmogorov-Arnold Network (KAN) in the QAS algorithm, analyzing their efficiency in the task of quantum state preparation and quantum chemistry. In quantum state preparation, our results show that in a noiseless scenario, the probability of success is 2 to 5 times higher than MLPs. In noisy environments, KAN outperforms MLPs in fidelity when approximating these states, showcasing its robustness against noise. In tackling quantum chemistry problems, we enhance the recently proposed QAS algorithm by integrating curriculum reinforcement learning with a KAN structure. This facilitates a more efficient design of parameterized quantum circuits by reducing the number of required 2-qubit gates and circuit depth. Further investigation reveals that KAN requires a significantly smaller number of learnable parameters compared to MLPs; however, the average time of executing each episode for KAN is higher.

SigKAN: Signature-Weighted Kolmogorov-Arnold Networks for Time Series

Authors: Hugo Inzirillo, Remi Genet

Citation Count: 12

Abstract: We propose a novel approach that enhances multivariate function approximation using learnable path signatures and Kolmogorov-Arnold networks (KANs). We enhance the learning capabilities of these networks by weighting the values obtained by KANs using learnable path signatures, which capture important geometric features of paths. This combination allows for a more comprehensive and flexible representation of sequential and temporal data. We demonstrate through studies that our SigKANs with learnable path signatures perform better than conventional methods across a range of function approximation challenges. By leveraging path signatures in neural networks, this method offers intriguing opportunities to enhance performance in time series analysis and time series forecasting, among other fields.

Kolmogorov-Arnold Graph Neural Networks

Authors: Gianluca De Carlo, Andrea Mastropietro, Aris Anagnostopoulos

Citation Count: 28

Abstract: Graph neural networks (GNNs) excel in learning from network-like data but often lack interpretability, making their application challenging in domains requiring transparent decision-making. We propose the Graph Kolmogorov-Arnold Network (GKAN), a novel GNN model leveraging spline-based activation functions on edges to enhance both accuracy and interpretability. Our experiments on five benchmark datasets demonstrate that GKAN outperforms state-of-the-art GNN models in node classification, link prediction, and graph classification tasks. In addition to the improved accuracy, GKAN’s design inherently provides clear insights into the model’s decision-making process, eliminating the need for post-hoc explainability techniques. This paper discusses the methodology, performance, and interpretability of GKAN, highlighting its potential for applications in domains where interpretability is crucial.

KAGNNs: Kolmogorov-Arnold Networks meet Graph Learning

Authors: Roman Bresson, Giannis Nikolentzos, George Panagopoulos, Michail Chatzianastasis, Jun Pang, Michalis Vazirgiannis

Citation Count: 49

Abstract: In recent years, Graph Neural Networks (GNNs) have become the de facto tool for learning node and graph representations. Most GNNs typically consist of a sequence of neighborhood aggregation (a.k.a., message-passing) layers, within which the representation of each node is updated based on those of its neighbors. The most expressive message-passing GNNs can be obtained through the use of the sum aggregator and of MLPs for feature transformation, thanks to their universal approximation capabilities. However, the limitations of MLPs recently motivated the introduction of another family of universal approximators, called Kolmogorov-Arnold Networks (KANs) which rely on a different representation theorem. In this work, we compare the performance of KANs against that of MLPs on graph learning tasks. We implement three new KAN-based GNN layers, inspired respectively by the GCN, GAT and GIN layers. We evaluate two different implementations of KANs using two distinct base families of functions, namely B-splines and radial basis functions. We perform extensive experiments on node classification, link prediction, graph classification and graph regression datasets. Our results indicate that KANs are on-par with or better than MLPs on all tasks studied in this paper. We also show that the size and training speed of RBF-based KANs is only marginally higher than for MLPs, making them viable alternatives. Code available at https://github.com/RomanBresson/KAGNN.

Finite basis Kolmogorov-Arnold networks: domain decomposition for data-driven and physics-informed problems

Authors: Amanda A. Howard, Bruno Jacob, Sarah Helfert, Alexander Heinlein, Panos Stinis

Citation Count: 28

Abstract: Kolmogorov-Arnold networks (KANs) have attracted attention recently as an alternative to multilayer perceptrons (MLPs) for scientific machine learning. However, KANs can be expensive to train, even for relatively small networks. Inspired by finite basis physics-informed neural networks (FBPINNs), in this work, we develop a domain decomposition method for KANs that allows for several small KANs to be trained in parallel to give accurate solutions for multiscale problems. We show that finite basis KANs (FBKANs) can provide accurate results with noisy data and for physics-informed training.

July

SpectralKAN: Weighted Activation Distribution Kolmogorov-Arnold Network for Hyperspectral Image Change Detection

Authors: Yanheng Wang, Xiaohan Yu, Yongsheng Gao, Jianjun Sha, Jian Wang, Shiyong Yan, Kai Qin, Yonggang Zhang, Lianru Gao

Citation Count: 7

Abstract: Kolmogorov-Arnold networks (KANs) represent data features by learning the activation functions and demonstrate superior accuracy with fewer parameters, FLOPs, GPU memory usage (Memory), shorter training time (TraT), and testing time (TesT) when handling low-dimensional data. However, when applied to high-dimensional data, which contains significant redundant information, the current activation mechanism of KANs leads to unnecessary computations, thereby reducing computational efficiency. KANs require reshaping high-dimensional data into a one-dimensional tensor as input, which inevitably results in the loss of dimensional information. To address these limitations, we propose weighted activation distribution KANs (WKANs), which reduce the frequency of activations per node and distribute node information into different output nodes through weights to avoid extracting redundant information. Furthermore, we introduce a multilevel tensor splitting framework (MTSF), which decomposes high-dimensional data to extract features from each dimension independently and leverages tensor-parallel computation to significantly improve the computational efficiency of WKANs on high-dimensional data. In this paper, we design SpectralKAN for hyperspectral image change detection using the proposed MTSF. SpectralKAN demonstrates outstanding performance across five datasets, achieving an overall accuracy (OA) of 0.9801 and a Kappa coefficient (K) of 0.9514 on the Farmland dataset, with only 8 k parameters, 0.07 M FLOPs, 911 MB Memory, 13.26 S TraT, and 2.52 S TesT, underscoring its superior accuracy-efficiency trade-off. The source code is publicly available at https://github.com/yanhengwang-heu/SpectralKAN.

Kolmogorov-Arnold Convolutions: Design Principles and Empirical Studies

Author: Ivan Drokin

Citation Count: 20

Abstract: The emergence of Kolmogorov-Arnold Networks (KANs) has sparked significant interest and debate within the scientific community. This paper explores the application of KANs in the domain of computer vision (CV). We examine the convolutional version of KANs, considering various nonlinearity options beyond splines, such as Wavelet transforms and a range of polynomials. We propose a parameter-efficient design for Kolmogorov-Arnold convolutional layers and a parameter-efficient finetuning algorithm for pre-trained KAN models, as well as KAN convolutional versions of self-attention and focal modulation layers. We provide empirical evaluations conducted on MNIST, CIFAR10, CIFAR100, Tiny ImageNet, ImageNet1k, and HAM10000 datasets for image classification tasks. Additionally, we explore segmentation tasks, proposing U-Net-like architectures with KAN convolutions, and achieving state-of-the-art results on BUSI, GlaS, and CVC datasets. We summarized all of our findings in a preliminary design guide of KAN convolutional models for computer vision tasks. Furthermore, we investigate regularization techniques for KANs. All experimental code and implementations of convolutional layers and models, pre-trained on ImageNet1k weights are available on GitHub via this https://github.com/IvanDrokin/torch-conv-kan

SineKAN: Kolmogorov-Arnold Networks Using Sinusoidal Activation Functions

Authors: Eric A. F. Reinhardt, P. R. Dinesh, Sergei Gleyzer

Venue: Frontiers Artif. Intell.

Citation Count: 12

Abstract: Recent work has established an alternative to traditional multi-layer perceptron neural networks in the form of Kolmogorov-Arnold Networks (KAN). The general KAN framework uses learnable activation functions on the edges of the computational graph followed by summation on nodes. The learnable edge activation functions in the original implementation are basis spline functions (B-Spline). Here, we present a model in which learnable grids of B-Spline activation functions are replaced by grids of re-weighted sine functions (SineKAN). We evaluate numerical performance of our model on a benchmark vision task. We show that our model can perform better than or comparable to B-Spline KAN models and an alternative KAN implementation based on periodic cosine and sine functions representing a Fourier Series. Further, we show that SineKAN has numerical accuracy that could scale comparably to dense neural networks (DNNs). Compared to the two baseline KAN models, SineKAN achieves a substantial speed increase at all hidden layer sizes, batch sizes, and depths. Current advantage of DNNs due to hardware and software optimizations are discussed along with theoretical scaling. Additionally, properties of SineKAN compared to other KAN implementations and current limitations are also discussed

KAN-ODEs: Kolmogorov-Arnold Network Ordinary Differential Equations for Learning Dynamical Systems and Hidden Physics

Authors: Benjamin C. Koenig, Suyong Kim, Sili Deng

Venue: Computer Methods in Applied Mechanics and Engineering

Citation Count: 54

Abstract: Kolmogorov-Arnold networks (KANs) as an alternative to multi-layer perceptrons (MLPs) are a recent development demonstrating strong potential for data-driven modeling. This work applies KANs as the backbone of a neural ordinary differential equation (ODE) framework, generalizing their use to the time-dependent and temporal grid-sensitive cases often seen in dynamical systems and scientific machine learning applications. The proposed KAN-ODEs retain the flexible dynamical system modeling framework of Neural ODEs while leveraging the many benefits of KANs compared to MLPs, including higher accuracy and faster neural scaling, stronger interpretability and generalizability, and lower parameter counts. First, we quantitatively demonstrated these improvements in a comprehensive study of the classical Lotka-Volterra predator-prey model. We then showcased the KAN-ODE framework’s ability to learn symbolic source terms and complete solution profiles in higher-complexity and data-lean scenarios including wave propagation and shock formation, the complex Schrödinger equation, and the Allen-Cahn phase separation equation. The successful training of KAN-ODEs, and their improved performance compared to traditional Neural ODEs, implies significant potential in leveraging this novel network architecture in myriad scientific machine learning applications for discovering hidden physics and predicting dynamic evolution.

RPN: Reconciled Polynomial Network Towards Unifying PGMs, Kernel SVMs, MLP and KAN

Author: Jiawei Zhang

Citation Count: 4

Abstract: In this paper, we will introduce a novel deep model named Reconciled Polynomial Network (RPN) for deep function learning. RPN has a very general architecture and can be used to build models with various complexities, capacities, and levels of completeness, which all contribute to the correctness of these models. As indicated in the subtitle, RPN can also serve as the backbone to unify different base models into one canonical representation. This includes non-deep models, like probabilistic graphical models (PGMs) - such as Bayesian network and Markov network - and kernel support vector machines (kernel SVMs), as well as deep models like the classic multi-layer perceptron (MLP) and the recent Kolmogorov-Arnold network (KAN). Technically, RPN proposes to disentangle the underlying function to be inferred into the inner product of a data expansion function and a parameter reconciliation function. Together with the remainder function, RPN accurately approximates the underlying functions that governs data distributions. The data expansion functions in RPN project data vectors from the input space to a high-dimensional intermediate space, specified by the expansion functions in definition. Meanwhile, RPN also introduces the parameter reconciliation functions to fabricate a small number of parameters into a higher-order parameter matrix to address the ``curse of dimensionality’’ problem caused by the data expansions. Moreover, the remainder functions provide RPN with additional complementary information to reduce potential approximation errors. We conducted extensive empirical experiments on numerous benchmark datasets across multiple modalities, including continuous function datasets, discrete vision and language datasets, and classic tabular datasets, to investigate the effectiveness of RPN.

HyperKAN: Kolmogorov-Arnold Networks make Hyperspectral Image Classificators Smarter

Authors: Valeriy Lobanov, Nikita Firsov, Evgeny Myasnikov, Roman Khabibullin, Artem Nikonorov

Citation Count: 8

Abstract: In traditional neural network architectures, a multilayer perceptron (MLP) is typically employed as a classification block following the feature extraction stage. However, the Kolmogorov-Arnold Network (KAN) presents a promising alternative to MLP, offering the potential to enhance prediction accuracy. In this paper, we propose the replacement of linear and convolutional layers of traditional networks with KAN-based counterparts. These modifications allowed us to significantly increase the per-pixel classification accuracy for hyperspectral remote-sensing images. We modified seven different neural network architectures for hyperspectral image classification and observed a substantial improvement in the classification accuracy across all the networks. The architectures considered in the paper include baseline MLP, state-of-the-art 1D (1DCNN) and 3D convolutional (two different 3DCNN, NM3DCNN), and transformer (SSFTT) architectures, as well as newly proposed M1DCNN. The greatest effect was achieved for convolutional networks working exclusively on spectral data, and the best classification quality was achieved using a KAN-based transformer architecture. All the experiments were conducted using seven openly available hyperspectral datasets. Our code is available at https://github.com/f-neumann77/HyperKAN.

TCKAN:A Novel Integrated Network Model for Predicting Mortality Risk in Sepsis Patients

Author: Fanglin Dong

Citation Count: 2

Abstract: Sepsis poses a major global health threat, accounting for millions of deaths annually and significant economic costs. Accurately predicting the risk of mortality in sepsis patients enables early identification, promotes the efficient allocation of medical resources, and facilitates timely interventions, thereby improving patient outcomes. Current methods typically utilize only one type of data–either constant, temporal, or ICD codes. This study introduces a novel approach, the Time-Constant Kolmogorov-Arnold Network (TCKAN), which uniquely integrates temporal data, constant data, and ICD codes within a single predictive model. Unlike existing methods that typically rely on one type of data, TCKAN leverages a multi-modal data integration strategy, resulting in superior predictive accuracy and robustness in identifying high-risk sepsis patients. Validated against the MIMIC-III and MIMIC-IV datasets, TCKAN surpasses existing machine learning and deep learning methods in accuracy, sensitivity, and specificity. Notably, TCKAN achieved AUCs of 87.76% and 88.07%, demonstrating superior capability in identifying high-risk patients. Additionally, TCKAN effectively combats the prevalent issue of data imbalance in clinical settings, improving the detection of patients at elevated risk of mortality and facilitating timely interventions. These results confirm the model’s effectiveness and its potential to transform patient management and treatment optimization in clinical practice. Although the TCKAN model has already incorporated temporal, constant, and ICD code data, future research could include more diverse medical data types, such as imaging and laboratory test results, to achieve a more comprehensive data integration and further improve predictive accuracy.

Enhancing Long-Range Dependency with State Space Model and Kolmogorov-Arnold Networks for Aspect-Based Sentiment Analysis

Authors: Adamu Lawan, Juhua Pu, Haruna Yunusa, Aliyu Umar, Muhammad Lawan

Citation Count: 5

Abstract: Aspect-based Sentiment Analysis (ABSA) evaluates sentiments toward specific aspects of entities within the text. However, attention mechanisms and neural network models struggle with syntactic constraints. The quadratic complexity of attention mechanisms also limits their adoption for capturing long-range dependencies between aspect and opinion words in ABSA. This complexity can lead to the misinterpretation of irrelevant contextual words, restricting their effectiveness to short-range dependencies. To address the above problem, we present a novel approach to enhance long-range dependencies between aspect and opinion words in ABSA (MambaForGCN). This approach incorporates syntax-based Graph Convolutional Network (SynGCN) and MambaFormer (Mamba-Transformer) modules to encode input with dependency relations and semantic information. The Multihead Attention (MHA) and Selective State Space model (Mamba) blocks in the MambaFormer module serve as channels to enhance the model with short and long-range dependencies between aspect and opinion words. We also introduce the Kolmogorov-Arnold Networks (KANs) gated fusion, an adaptive feature representation system that integrates SynGCN and MambaFormer and captures non-linear, complex dependencies. Experimental results on three benchmark datasets demonstrate MambaForGCN’s effectiveness, outperforming state-of-the-art (SOTA) baseline models.

Kolmogorov-Arnold Networks: A Critical Assessment of Claims, Performance, and Practical Viability

Authors: Yuntian Hou, Tianrui Ji, Di Zhang, Angelos Stefanidis

Citation Count: 31

Abstract: Kolmogorov-Arnold Networks (KANs) have gained significant attention as an alternative to traditional multilayer perceptrons, with proponents claiming superior interpretability and performance through learnable univariate activation functions. However, recent systematic evaluations reveal substantial discrepancies between theoretical claims and empirical evidence. This critical assessment examines KANs’ actual performance across diverse domains using fair comparison methodologies that control for parameters and computational costs. Our analysis demonstrates that KANs outperform MLPs only in symbolic regression tasks, while consistently underperforming in machine learning, computer vision, and natural language processing benchmarks. The claimed advantages largely stem from B-spline activation functions rather than architectural innovations, and computational overhead (1.36-100x slower) severely limits practical deployment. Furthermore, theoretical claims about breaking the “curse of dimensionality” lack rigorous mathematical foundation. We systematically identify the conditions under which KANs provide value versus traditional approaches, establish evaluation standards for future research, and propose a priority-based roadmap for addressing fundamental limitations. This work provides researchers and practitioners with evidence-based guidance for the rational adoption of KANs while highlighting critical research gaps that must be addressed for broader applicability.

DP-KAN: Differentially Private Kolmogorov-Arnold Networks

Authors: Nikita P. Kalinin, Simone Bombari, Hossein Zakerinia, Christoph H. Lampert

Citation Count: 1

Abstract: We study the Kolmogorov-Arnold Network (KAN), recently proposed as an alternative to the classical Multilayer Perceptron (MLP), in the application for differentially private model training. Using the DP-SGD algorithm, we demonstrate that KAN can be made private in a straightforward manner and evaluated its performance across several datasets. Our results indicate that the accuracy of KAN is not only comparable with MLP but also experiences similar deterioration due to privacy constraints, making it suitable for differentially private model training.

A Survey on Universal Approximation Theorems

Author: Midhun T Augustine

Citation Count: 4

Abstract: This paper discusses various theorems on the approximation capabilities of neural networks (NNs), which are known as universal approximation theorems (UATs). The paper gives a systematic overview of UATs starting from the preliminary results on function approximation, such as Taylor’s theorem, Fourier’s theorem, Weierstrass approximation theorem, Kolmogorov - Arnold representation theorem, etc. Theoretical and numerical aspects of UATs are covered from both arbitrary width and depth.

DropKAN: Regularizing KANs by masking post-activations

Author: Mohammed Ghaith Altarabichi

Citation Count: 10

Abstract: We propose DropKAN (Dropout Kolmogorov-Arnold Networks) a regularization method that prevents co-adaptation of activation function weights in Kolmogorov-Arnold Networks (KANs). DropKAN functions by embedding the drop mask directly within the KAN layer, randomly masking the outputs of some activations within the KANs’ computation graph. We show that this simple procedure that require minimal coding effort has a regularizing effect and consistently lead to better generalization of KANs. We analyze the adaptation of the standard Dropout with KANs and demonstrate that Dropout applied to KANs’ neurons can lead to unpredictable behavior in the feedforward pass. We carry an empirical study with real world Machine Learning datasets to validate our findings. Our results suggest that DropKAN is consistently a better alternative to using standard Dropout with KANs, and improves the generalization performance of KANs. Our implementation of DropKAN is available at: \url{https://github.com/Ghaith81/dropkan}.

Reduced Effectiveness of Kolmogorov-Arnold Networks on Functions with Noise

Authors: Haoran Shen, Chen Zeng, Jiahui Wang, Qiao Wang

Venue: IEEE International Conference on Acoustics, Speech, and Signal Processing

Citation Count: 12

Abstract: It has been observed that even a small amount of noise introduced into the dataset can significantly degrade the performance of KAN. In this brief note, we aim to quantitatively evaluate the performance when noise is added to the dataset. We propose an oversampling technique combined with denoising to alleviate the impact of noise. Specifically, we employ kernel filtering based on diffusion maps for pre-filtering the noisy data for training KAN network. Our experiments show that while adding i.i.d. noise with any fixed SNR, when we increase the amount of training data by a factor of $r$, the test-loss (RMSE) of KANs will exhibit a performance trend like $\text{test-loss} \sim \mathcal{O}(r^{-\frac{1}{2}})$ as $r\to +\infty$. We conclude that applying both oversampling and filtering strategies can reduce the detrimental effects of noise. Nevertheless, determining the optimal variance for the kernel filtering process is challenging, and enhancing the volume of training data substantially increases the associated costs, because the training dataset needs to be expanded multiple times in comparison to the initial clean data. As a result, the noise present in the data ultimately diminishes the effectiveness of Kolmogorov-Arnold networks.

Deep State Space Recurrent Neural Networks for Time Series Forecasting

Author: Hugo Inzirillo

Citation Count: 6

Abstract: We explore various neural network architectures for modeling the dynamics of the cryptocurrency market. Traditional linear models often fall short in accurately capturing the unique and complex dynamics of this market. In contrast, Deep Neural Networks (DNNs) have demonstrated considerable proficiency in time series forecasting. This papers introduces novel neural network framework that blend the principles of econometric state space models with the dynamic capabilities of Recurrent Neural Networks (RNNs). We propose state space models using Long Short Term Memory (LSTM), Gated Residual Units (GRU) and Temporal Kolmogorov-Arnold Networks (TKANs). According to the results, TKANs, inspired by Kolmogorov-Arnold Networks (KANs) and LSTM, demonstrate promising outcomes.

Inferring turbulent velocity and temperature fields and their statistics from Lagrangian velocity measurements using physics-informed Kolmogorov-Arnold Networks

Authors: Juan Diego Toscano, Theo Käufer, Zhibo Wang, Martin Maxey, Christian Cierpka, George Em Karniadakis

Citation Count: 16

Abstract: We propose the Artificial Intelligence Velocimetry-Thermometry (AIVT) method to infer hidden temperature fields from experimental turbulent velocity data. This physics-informed machine learning method enables us to infer continuous temperature fields using only sparse velocity data, hence eliminating the need for direct temperature measurements. Specifically, AIVT is based on physics-informed Kolmogorov-Arnold Networks (not neural networks) and is trained by optimizing a combined loss function that minimizes the residuals of the velocity data, boundary conditions, and the governing equations. We apply AIVT to a unique set of experimental volumetric and simultaneous temperature and velocity data of Rayleigh-Bénard convection (RBC) that we acquired by combining Particle Image Thermometry and Lagrangian Particle Tracking. This allows us to compare AIVT predictions and measurements directly. We demonstrate that we can reconstruct and infer continuous and instantaneous velocity and temperature fields from sparse experimental data at a fidelity comparable to direct numerical simulations (DNS) of turbulence. This, in turn, enables us to compute important quantities for quantifying turbulence, such as fluctuations, viscous and thermal dissipation, and QR distribution. This paradigm shift in processing experimental data using AIVT to infer turbulent fields at DNS-level fidelity is a promising avenue in breaking the current deadlock of quantitative understanding of turbulence at high Reynolds numbers, where DNS is computationally infeasible.

Sparks of Quantum Advantage and Rapid Retraining in Machine Learning

Author: William Troy

Citation Count: 5

Abstract: The advent of quantum computing holds the potential to revolutionize various fields by solving complex problems more efficiently than classical computers. Despite this promise, practical quantum advantage is hindered by current hardware limitations, notably the small number of qubits and high noise levels. In this study, we leverage adiabatic quantum computers to optimize Kolmogorov-Arnold Networks, a powerful neural network architecture for representing complex functions with minimal parameters. By modifying the network to use Bezier curves as the basis functions and formulating the optimization problem into a Quadratic Unconstrained Binary Optimization problem, we create a fixed-sized solution space, independent of the number of training samples. This strategy allows for the optimization of an entire neural network in a single training iteration in which, due to order of operations, a majority of the processing is done using a collapsed version of the training dataset. This inherently creates extremely fast training speeds, which are validated experimentally, compared to classical optimizers including Adam, Stochastic Gradient Descent, Adaptive Gradient, and simulated annealing. Additionally, we introduce a novel rapid retraining capability, enabling the network to be retrained with new data without reprocessing old samples, thus enhancing learning efficiency in dynamic environments. Experiments on retraining demonstrate a hundred times speed up using adiabatic quantum computing based optimization compared to that of the gradient descent based optimizers, with theoretical models allowing this speed up to be much larger! Our findings suggest that with further advancements in quantum hardware and algorithm optimization, quantum-optimized machine learning models could have broad applications across various domains, with initial focus on rapid retraining.

Image Classification using Fuzzy Pooling in Convolutional Kolmogorov-Arnold Networks

Authors: Ayan Igali, Pakizar Shamoi

Venue: 2024 Joint 13th International Conference on Soft Computing and Intelligent Systems and 25th International Symposium on Advanced Intelligent Systems (SCIS&ISIS)

Citation Count: 3

Abstract: Nowadays, deep learning models are increasingly required to be both interpretable and highly accurate. We present an approach that integrates Kolmogorov-Arnold Network (KAN) classification heads and Fuzzy Pooling into convolutional neural networks (CNNs). By utilizing the interpretability of KAN and the uncertainty handling capabilities of fuzzy logic, the integration shows potential for improved performance in image classification tasks. Our comparative analysis demonstrates that the modified CNN architecture with KAN and Fuzzy Pooling achieves comparable or higher accuracy than traditional models. The findings highlight the effectiveness of combining fuzzy logic and KAN to develop more interpretable and efficient deep learning models. Future work will aim to expand this approach across larger datasets.

KAN or MLP: A Fairer Comparison

Authors: Runpeng Yu, Weihao Yu, Xinchao Wang

Abstract: This paper does not introduce a novel method. Instead, it offers a fairer and more comprehensive comparison of KAN and MLP models across various tasks, including machine learning, computer vision, audio processing, natural language processing, and symbolic formula representation. Specifically, we control the number of parameters and FLOPs to compare the performance of KAN and MLP. Our main observation is that, except for symbolic formula representation tasks, MLP generally outperforms KAN. We also conduct ablation studies on KAN and find that its advantage in symbolic formula representation mainly stems from its B-spline activation function. When B-spline is applied to MLP, performance in symbolic formula representation significantly improves, surpassing or matching that of KAN. However, in other tasks where MLP already excels over KAN, B-spline does not substantially enhance MLP’s performance. Furthermore, we find that KAN’s forgetting issue is more severe than that of MLP in a standard class-incremental continual learning setting, which differs from the findings reported in the KAN paper. We hope these results provide insights for future research on KAN and other MLP alternatives. Project link: https://github.com/yu-rp/KANbeFair

2D and 3D Deep Learning Models for MRI-based Parkinson’s Disease Classification: A Comparative Analysis of Convolutional Kolmogorov-Arnold Networks, Convolutional Neural Networks, and Graph Convolutional Networks

Authors: Salil B Patel, Vicky Goh, James F FitzGerald, Chrystalina A Antoniades

Citation Count: 3

Abstract: Parkinson’s Disease (PD) diagnosis remains challenging. This study applies Convolutional Kolmogorov-Arnold Networks (ConvKANs), integrating learnable spline-based activation functions into convolutional layers, for PD classification using structural MRI. The first 3D implementation of ConvKANs for medical imaging is presented, comparing their performance to Convolutional Neural Networks (CNNs) and Graph Convolutional Networks (GCNs) across three open-source datasets. Isolated analyses assessed performance within individual datasets, using cross-validation techniques. Holdout analyses evaluated cross-dataset generalizability by training models on two datasets and testing on the third, mirroring real-world clinical scenarios. In isolated analyses, 2D ConvKANs achieved the highest AUC of 0.99 (95% CI: 0.98-0.99) on the PPMI dataset, outperforming 2D CNNs (AUC: 0.97, p = 0.0092). 3D models showed promise, with 3D CNN and 3D ConvKAN reaching an AUC of 0.85 on PPMI. In holdout analyses, 3D ConvKAN demonstrated superior generalization, achieving an AUC of 0.85 on early-stage PD data. GCNs underperformed in 2D but improved in 3D implementations. These findings highlight ConvKANs’ potential for PD detection, emphasize the importance of 3D analysis in capturing subtle brain changes, and underscore cross-dataset generalization challenges. This study advances AI-assisted PD diagnosis using structural MRI and emphasizes the need for larger-scale validation.

Adaptive Training of Grid-Dependent Physics-Informed Kolmogorov-Arnold Networks

Authors: Spyros Rigas, Michalis Papachristou, Theofilos Papadopoulos, Fotios Anagnostopoulos, Georgios Alexandridis

Venue: IEEE Access

Citation Count: 24

Abstract: Physics-Informed Neural Networks (PINNs) have emerged as a robust framework for solving Partial Differential Equations (PDEs) by approximating their solutions via neural networks and imposing physics-based constraints on the loss function. Traditionally, Multilayer Perceptrons (MLPs) have been the neural network of choice, with significant progress made in optimizing their training. Recently, Kolmogorov-Arnold Networks (KANs) were introduced as a viable alternative, with the potential of offering better interpretability and efficiency while requiring fewer parameters. In this paper, we present a fast JAX-based implementation of grid-dependent Physics-Informed Kolmogorov-Arnold Networks (PIKANs) for solving PDEs, achieving up to 84 times faster training times than the original KAN implementation. We propose an adaptive training scheme for PIKANs, introducing an adaptive state transition technique to avoid loss function peaks between grid extensions, and a methodology for designing PIKANs with alternative basis functions. Through comparative experiments, we demonstrate that the adaptive features significantly enhance solution accuracy, decreasing the L^2 error relative to the reference solution by up to 43.02%. For the studied PDEs, our methodology approaches or surpasses the results obtained from architectures that utilize up to 8.5 times more parameters, highlighting the potential of adaptive, grid-dependent PIKANs as a superior alternative in scientific and engineering applications.

Kolmogorov–Arnold networks in molecular dynamics

Authors: Yuki Nagai, Masahiko Okumura

Citation Count: 3

Abstract: We explore the integration of Kolmogorov Networks (KANs) into molecular dynamics (MD) simulations to improve interatomic potentials. We propose that widely used potentials, such as the Lennard-Jones (LJ) potential, the embedded atom model (EAM), and artificial neural network (ANN) potentials, can be interpreted within the KAN framework. Specifically, we demonstrate that the descriptors for ANN potentials, typically constructed using polynomials, can be redefined using KAN’s non-linear functions. By employing linear or cubic spline interpolations for these KAN functions, we show that the computational cost of evaluating ANN potentials and their derivatives is reduced.

Exploring the Limitations of Kolmogorov-Arnold Networks in Classification: Insights to Software Training and Hardware Implementation

Authors: Van Duy Tran, Tran Xuan Hieu Le, Thi Diem Tran, Hoai Luan Pham, Vu Trung Duong Le, Tuan Hai Vu, Van Tinh Nguyen, Yasuhiko Nakashima

Venue: 2024 Twelfth International Symposium on Computing and Networking Workshops (CANDARW)

Citation Count: 16

Abstract: Kolmogorov-Arnold Networks (KANs), a novel type of neural network, have recently gained popularity and attention due to the ability to substitute multi-layer perceptions (MLPs) in artificial intelligence (AI) with higher accuracy and interoperability. However, KAN assessment is still limited and cannot provide an in-depth analysis of a specific domain. Furthermore, no study has been conducted on the implementation of KANs in hardware design, which would directly demonstrate whether KANs are truly superior to MLPs in practical applications. As a result, in this paper, we focus on verifying KANs for classification issues, which are a common but significant topic in AI using four different types of datasets. Furthermore, the corresponding hardware implementation is considered using the Vitis high-level synthesis (HLS) tool. To the best of our knowledge, this is the first article to implement hardware for KAN. The results indicate that KANs cannot achieve more accuracy than MLPs in high complex datasets while utilizing substantially higher hardware resources. Therefore, MLP remains an effective approach for achieving accuracy and efficiency in software and hardware implementation.

Physics Informed Kolmogorov-Arnold Neural Networks for Dynamical Analysis via Efficent-KAN and WAV-KAN

Authors: Subhajit Patra, Sonali Panda, Bikram Keshari Parida, Mahima Arya, Kurt Jacobs, Denys I. Bondar, Abhijit Sen

Citation Count: 12

Abstract: Physics-informed neural networks have proven to be a powerful tool for solving differential equations, leveraging the principles of physics to inform the learning process. However, traditional deep neural networks often face challenges in achieving high accuracy without incurring significant computational costs. In this work, we implement the Physics-Informed Kolmogorov-Arnold Neural Networks (PIKAN) through efficient-KAN and WAV-KAN, which utilize the Kolmogorov-Arnold representation theorem. PIKAN demonstrates superior performance compared to conventional deep neural networks, achieving the same level of accuracy with fewer layers and reduced computational overhead. We explore both B-spline and wavelet-based implementations of PIKAN and benchmark their performance across various ordinary and partial differential equations using unsupervised (data-free) and supervised (data-driven) techniques. For certain differential equations, the data-free approach suffices to find accurate solutions, while in more complex scenarios, the data-driven method enhances the PIKAN’s ability to converge to the correct solution. We validate our results against numerical solutions and achieve $99 \%$ accuracy in most scenarios.

Gaussian Process Kolmogorov-Arnold Networks

Author: Andrew Siyuan Chen

Abstract: In this paper, we introduce a probabilistic extension to Kolmogorov Arnold Networks (KANs) by incorporating Gaussian Process (GP) as non-linear neurons, which we refer to as GP-KAN. A fully analytical approach to handling the output distribution of one GP as an input to another GP is achieved by considering the function inner product of a GP function sample with the input distribution. These GP neurons exhibit robust non-linear modelling capabilities while using few parameters and can be easily and fully integrated in a feed-forward network structure. They provide inherent uncertainty estimates to the model prediction and can be trained directly on the log-likelihood objective function, without needing variational lower bounds or approximations. In the context of MNIST classification, a model based on GP-KAN of 80 thousand parameters achieved 98.5% prediction accuracy, compared to current state-of-the-art models with 1.5 million parameters.

F-KANs: Federated Kolmogorov-Arnold Networks

Authors: Engin Zeydan, Cristian J. Vaca-Rubio, Luis Blanco, Roberto Pereira, Marius Caus, Abdullah Aydeger

Venue: Consumer Communications and Networking Conference

Citation Count: 8

Abstract: In this paper, we present an innovative federated learning (FL) approach that utilizes Kolmogorov-Arnold Networks (KANs) for classification tasks. By utilizing the adaptive activation capabilities of KANs in a federated framework, we aim to improve classification capabilities while preserving privacy. The study evaluates the performance of federated KANs (F- KANs) compared to traditional Multi-Layer Perceptrons (MLPs) on classification task. The results show that the F-KANs model significantly outperforms the federated MLP model in terms of accuracy, precision, recall, F1 score and stability, and achieves better performance, paving the way for more efficient and privacy-preserving predictive analytics.

COEFF-KANs: A Paradigm to Address the Electrolyte Field with KANs

Authors: Xinhe Li, Zhuoying Feng, Yezeng Chen, Weichen Dai, Zixu He, Yi Zhou, Shuhong Jiao

Citation Count: 8

Abstract: To reduce the experimental validation workload for chemical researchers and accelerate the design and optimization of high-energy-density lithium metal batteries, we aim to leverage models to automatically predict Coulombic Efficiency (CE) based on the composition of liquid electrolytes. There are mainly two representative paradigms in existing methods: machine learning and deep learning. However, the former requires intelligent input feature selection and reliable computational methods, leading to error propagation from feature estimation to model prediction, while the latter (e.g. MultiModal-MoLFormer) faces challenges of poor predictive performance and overfitting due to limited diversity in augmented data. To tackle these issues, we propose a novel method COEFF (COlumbic EFficiency prediction via Fine-tuned models), which consists of two stages: pre-training a chemical general model and fine-tuning on downstream domain data. Firstly, we adopt the publicly available MoLFormer model to obtain feature vectors for each solvent and salt in the electrolyte. Then, we perform a weighted average of embeddings for each token across all molecules, with weights determined by the respective electrolyte component ratios. Finally, we input the obtained electrolyte features into a Multi-layer Perceptron or Kolmogorov-Arnold Network to predict CE. Experimental results on a real-world dataset demonstrate that our method achieves SOTA for predicting CE compared to all baselines. Data and code used in this work will be made publicly available after the paper is published.

Rethinking the Function of Neurons in KANs

Author: Mohammed Ghaith Altarabichi

Citation Count: 6

Abstract: The neurons of Kolmogorov-Arnold Networks (KANs) perform a simple summation motivated by the Kolmogorov-Arnold representation theorem, which asserts that sum is the only fundamental multivariate function. In this work, we investigate the potential for identifying an alternative multivariate function for KAN neurons that may offer increased practical utility. Our empirical research involves testing various multivariate functions in KAN neurons across a range of benchmark Machine Learning tasks. Our findings indicate that substituting the sum with the average function in KAN neurons results in significant performance enhancements compared to traditional KANs. Our study demonstrates that this minor modification contributes to the stability of training by confining the input to the spline within the effective range of the activation function. Our implementation and experiments are available at: \url{https://github.com/Ghaith81/dropkan}

From Complexity to Clarity: Kolmogorov-Arnold Networks in Nuclear Binding Energy Prediction

Authors: Hao Liu, Jin Lei, Zhongzhou Ren

Citation Count: 4

Abstract: This study explores the application of Kolmogorov-Arnold Networks (KANs) in predicting nuclear binding energies, leveraging their ability to decompose complex multi-parameter systems into simpler univariate functions. By utilizing data from the Atomic Mass Evaluation (AME2020) and incorporating features such as atomic number, neutron number, and shell effects, KANs achieved a significant lower root mean square error (0.26~MeV), surpassing traditional models. The symbolic regression analysis yielded simplified analytical expressions for binding energies, aligning with classical models like the liquid drop model and the Bethe-Weizsäcker formula. These results highlight KANs’ potential in enhancing the interpretability and understanding of nuclear phenomena, paving the way for future applications in nuclear physics and beyond.

DKL-KAN: Scalable Deep Kernel Learning using Kolmogorov-Arnold Networks

Authors: Shrenik Zinage, Sudeepta Mondal, Soumalya Sarkar

Citation Count: 7

Abstract: The need for scalable and expressive models in machine learning is paramount, particularly in applications requiring both structural depth and flexibility. Traditional deep learning methods, such as multilayer perceptrons (MLP), offer depth but lack ability to integrate structural characteristics of deep learning architectures with non-parametric flexibility of kernel methods. To address this, deep kernel learning (DKL) was introduced, where inputs to a base kernel are transformed using a deep learning architecture. These kernels can replace standard kernels, allowing both expressive power and scalability. The advent of Kolmogorov-Arnold Networks (KAN) has generated considerable attention and discussion among researchers in scientific domain. In this paper, we introduce a scalable deep kernel using KAN (DKL-KAN) as an effective alternative to DKL using MLP (DKL-MLP). Our approach involves simultaneously optimizing these kernel attributes using marginal likelihood within a Gaussian process framework. We analyze two variants of DKL-KAN for a fair comparison with DKL-MLP: one with same number of neurons and layers as DKL-MLP, and another with approximately same number of trainable parameters. To handle large datasets, we use kernel interpolation for scalable structured Gaussian processes (KISS-GP) for low-dimensional inputs and KISS-GP with product kernels for high-dimensional inputs. The efficacy of DKL-KAN is evaluated in terms of computational training time and test prediction accuracy across a wide range of applications. Additionally, the effectiveness of DKL-KAN is also examined in modeling discontinuities and accurately estimating prediction uncertainty. The results indicate that DKL-KAN outperforms DKL-MLP on datasets with a low number of observations. Conversely, DKL-MLP exhibits better scalability and higher test prediction accuracy on datasets with large number of observations.

August

TASI Lectures on Physics for Machine Learning

Author: Jim Halverson

Citation Count: 1

Abstract: These notes are based on lectures I gave at TASI 2024 on Physics for Machine Learning. The focus is on neural network theory, organized according to network expressivity, statistics, and dynamics. I present classic results such as the universal approximation theorem and neural network / Gaussian process correspondence, and also more recent results such as the neural tangent kernel, feature learning with the maximal update parameterization, and Kolmogorov-Arnold networks. The exposition on neural network theory emphasizes a field theoretic perspective familiar to theoretical physicists. I elaborate on connections between the two, including a neural network approach to field theory.

UKAN-EP: Enhancing U-KAN with Efficient Attention and Pyramid Aggregation for 3D Multi-Modal MRI Brain Tumor Segmentation

Authors: Yanbing Chen, Tianze Tang, Taehyo Kim, Hai Shu

Citation Count: 11

Abstract: Background: Gliomas are among the most common malignant brain tumors and exhibit substantial heterogeneity, complicating accurate detection and segmentation. Although multi-modal MRI is the clinical standard for glioma imaging, variability across modalities and high computational demands hamper effective automated segmentation. Methods: We propose UKAN-EP, a novel 3D extension of the original 2D U-KAN model for multi-modal MRI brain tumor segmentation. While U-KAN integrates Kolmogorov-Arnold Network (KAN) layers into a U-Net backbone, UKAN-EP further incorporates Efficient Channel Attention (ECA) and Pyramid Feature Aggregation (PFA) modules to enhance inter-modality feature fusion and multi-scale feature representation. We also introduce a dynamic loss weighting strategy that adaptively balances cross-entropy and Dice losses during training. Results: On the 2024 BraTS-GLI dataset, UKAN-EP achieves superior segmentation performance (e.g., Dice = 0.9001 $\pm$ 0.0127 and IoU = 0.8257 $\pm$ 0.0186 for the whole tumor) while requiring substantially fewer computational resources (223.57 GFLOPs and 11.30M parameters) compared to strong baselines including U-Net, Attention U-Net, Swin UNETR, VT-Unet, TransBTS, and 3D U-KAN. An extensive ablation study further confirms the effectiveness of ECA and PFA and shows the limited utility of self-attention and spatial attention alternatives. Conclusion: UKAN-EP demonstrates that combining the expressive power of KAN layers with lightweight channel-wise attention and multi-scale feature aggregation improves the accuracy and efficiency of brain tumor segmentation.

GNN-SKAN: Harnessing the Power of SwallowKAN to Advance Molecular Representation Learning with GNNs

Authors: Ruifeng Li, Mingqian Li, Wei Liu, Hongyang Chen

Citation Count: 3

Abstract: Effective molecular representation learning is crucial for advancing molecular property prediction and drug design. Mainstream molecular representation learning approaches are based on Graph Neural Networks (GNNs). However, these approaches struggle with three significant challenges: insufficient annotations, molecular diversity, and architectural limitations such as over-squashing, which leads to the loss of critical structural details. To address these challenges, we introduce a new class of GNNs that integrates the Kolmogorov-Arnold Networks (KANs), known for their robust data-fitting capabilities and high accuracy in small-scale AI + Science tasks. By incorporating KANs into GNNs, our model enhances the representation of molecular structures. We further advance this approach with a variant called SwallowKAN (SKAN), which employs adaptive Radial Basis Functions (RBFs) as the core of the non-linear neurons. This innovation improves both computational efficiency and adaptability to diverse molecular structures. Building on the strengths of SKAN, we propose a new class of GNNs, GNN-SKAN, and its augmented variant, GNN-SKAN+, which incorporates a SKAN-based classifier to further boost performance. To our knowledge, this is the first work to integrate KANs into GNN architectures tailored for molecular representation learning. Experiments across 6 classification datasets, 6 regression datasets, and 4 few-shot learning datasets demonstrate that our approach achieves new state-of-the-art performance in terms of accuracy and computational cost.

KAN based Autoencoders for Factor Models

Authors: Tianqi Wang, Shubham Singh

Citation Count: 1

Abstract: Inspired by recent advances in Kolmogorov-Arnold Networks (KANs), we introduce a novel approach to latent factor conditional asset pricing models. While previous machine learning applications in asset pricing have predominantly used Multilayer Perceptrons with ReLU activation functions to model latent factor exposures, our method introduces a KAN-based autoencoder which surpasses MLP models in both accuracy and interpretability. Our model offers enhanced flexibility in approximating exposures as nonlinear functions of asset characteristics, while simultaneously providing users with an intuitive framework for interpreting latent factors. Empirical backtesting demonstrates our model’s superior ability to explain cross-sectional risk exposures. Moreover, long-short portfolios constructed using our model’s predictions achieve higher Sharpe ratios, highlighting its practical value in investment management.

Bayesian Kolmogorov Arnold Networks (Bayesian_KANs): A Probabilistic Approach to Enhance Accuracy and Interpretability

Author: Masoud Muhammed Hassan

Citation Count: 3

Abstract: Because of its strong predictive skills, deep learning has emerged as an essential tool in many industries, including healthcare. Traditional deep learning models, on the other hand, frequently lack interpretability and omit to take prediction uncertainty into account two crucial components of clinical decision making. In order to produce explainable and uncertainty aware predictions, this study presents a novel framework called Bayesian Kolmogorov Arnold Networks (BKANs), which combines the expressive capacity of Kolmogorov Arnold Networks with Bayesian inference. We employ BKANs on two medical datasets, which are widely used benchmarks for assessing machine learning models in medical diagnostics: the Pima Indians Diabetes dataset and the Cleveland Heart Disease dataset. Our method provides useful insights into prediction confidence and decision boundaries and outperforms traditional deep learning models in terms of prediction accuracy. Moreover, BKANs’ capacity to represent aleatoric and epistemic uncertainty guarantees doctors receive more solid and trustworthy decision support. Our Bayesian strategy improves the interpretability of the model and considerably minimises overfitting, which is important for tiny and imbalanced medical datasets, according to experimental results. We present possible expansions to further use BKANs in more complicated multimodal datasets and address the significance of these discoveries for future research in building reliable AI systems for healthcare. This work paves the way for a new paradigm in deep learning model deployment in vital sectors where transparency and reliability are crucial.

KAN we improve on HEP classification tasks? Kolmogorov-Arnold Networks applied to an LHC physics example

Authors: Johannes Erdmann, Florian Mausolf, Jan Lukas Späh

Venue: Computing and Software for Big Science

Citation Count: 4

Abstract: Recently, Kolmogorov-Arnold Networks (KANs) have been proposed as an alternative to multilayer perceptrons, suggesting advantages in performance and interpretability. We study a typical binary event classification task in high-energy physics including high-level features and comment on the performance and interpretability of KANs in this context. Consistent with expectations, we find that the learned activation functions of a one-layer KAN resemble the univariate log-likelihood ratios of the respective input features. In deeper KANs, the activations in the first layer differ from those in the one-layer KAN, which indicates that the deeper KANs learn more complex representations of the data, a pattern commonly observed in other deep-learning architectures. We study KANs with different depths and widths and we compare them to multilayer perceptrons in terms of performance and number of trainable parameters. For the chosen classification task, we do not find that KANs are more parameter efficient. However, small KANs may offer advantages in terms of interpretability that come at the cost of only a moderate loss in performance.

Kolmogorov-Arnold PointNet: Deep learning for prediction of fluid fields on irregular geometries

Author: Ali Kashefi

Citation Count: 5

Abstract: Kolmogorov-Arnold Networks (KANs) have emerged as a promising alternative to traditional Multilayer Perceptrons (MLPs) in deep learning. KANs have already been integrated into various architectures, such as convolutional neural networks, graph neural networks, and transformers, and their potential has been assessed for predicting physical quantities. However, the combination of KANs with point-cloud-based neural networks (e.g., PointNet) for computational physics has not yet been explored. To address this, we present Kolmogorov-Arnold PointNet (KA-PointNet) as a novel supervised deep learning framework for the prediction of incompressible steady-state fluid flow fields in irregular domains, where the predicted fields are a function of the geometry of the domains. In KA-PointNet, we implement shared KANs in the segmentation branch of the PointNet architecture. We utilize Jacobi polynomials to construct shared KANs. As a benchmark test case, we consider incompressible laminar steady-state flow over a cylinder, where the geometry of its cross-section varies over the data set. We investigate the performance of Jacobi polynomials with different degrees as well as special cases of Jacobi polynomials such as Legendre polynomials, Chebyshev polynomials of the first and second kinds, and Gegenbauer polynomials, in terms of the computational cost of training and accuracy of prediction of the test set. Additionally, we compare the performance of PointNet with shared KANs (i.e., KA-PointNet) and PointNet with shared MLPs. It is observed that when the number of trainable parameters is approximately equal, PointNet with shared KANs (i.e., KA-PointNet) outperforms PointNet with shared MLPs. Moreover, KA-PointNet predicts the pressure and velocity distributions along the surface of cylinders more accurately, resulting in more precise computations of lift and drag.

Path-SAM2: Transfer SAM2 for digital pathology semantic segmentation

Authors: Mingya Zhang, Liang Wang, Zhihao Chen, Yiyuan Ge, Xianping Tao

Citation Count: 3

Abstract: The semantic segmentation task in pathology plays an indispensable role in assisting physicians in determining the condition of tissue lesions. With the proposal of Segment Anything Model (SAM), more and more foundation models have seen rapid development in the field of image segmentation. Recently, SAM2 has garnered widespread attention in both natural image and medical image segmentation. Compared to SAM, it has significantly improved in terms of segmentation accuracy and generalization performance. We compared the foundational models based on SAM and found that their performance in semantic segmentation of pathological images was hardly satisfactory. In this paper, we propose Path-SAM2, which for the first time adapts the SAM2 model to cater to the task of pathological semantic segmentation. We integrate the largest pretrained vision encoder for histopathology (UNI) with the original SAM2 encoder, adding more pathology-based prior knowledge. Additionally, we introduce a learnable Kolmogorov-Arnold Networks (KAN) classification module to replace the manual prompt process. In three adenoma pathological datasets, Path-SAM2 has achieved state-of-the-art performance.This study demonstrates the great potential of adapting SAM2 to pathology image segmentation tasks. We plan to release the code and model weights for this paper at: https://github.com/simzhangbest/SAM2PATH

Neural Network Modeling of Heavy-Quark Potential from Holography

Authors: Ou-Yang Luo, Xun Chen, Fu-Peng Li, Xiao-Hua Li, Kai Zhou

Citation Count: 3

Abstract: Using Multi-Layer Perceptrons (MLP) and Kolmogorov-Arnold Networks (KAN), we construct a holographic model based on lattice QCD data for the heavy-quark potential in the 2+1 system. The deformation factor $w(r)$ in the metric is obtained using the two types of neural network. First, we numerically obtain $w(r)$ using MLP, accurately reproducing the QCD results of the lattice, and calculate the heavy quark potential at finite temperature and the chemical potential. Subsequently, we employ KAN within the Andreev-Zakharov model for validation purpose, which can analytically reconstruct $w(r)$, matching the Andreev-Zakharov model exactly and confirming the validity of MLP. Finally, we construct an analytical holographic model using KAN and study the heavy-quark potential at finite temperature and chemical potential using the KAN-based holographic model. This work demonstrates the potential of KAN to derive analytical expressions for high-energy physics applications.

From Black Box to Clarity: AI-Powered Smart Grid Optimization with Kolmogorov-Arnold Networks

Authors: Xiaoting Wang, Yuzhuo Li, Yunwei Li, Gregory Kish

Venue: European Conference on Cognitive Ergonomics

Citation Count: 4

Abstract: This work is the first to adopt Kolmogorov-Arnold Networks (KAN), a recent breakthrough in artificial intelligence, for smart grid optimizations. To fully leverage KAN’s interpretability, a general framework is proposed considering complex uncertainties. The stochastic optimal power flow problem in hybrid AC/DC systems is chosen as a particularly tough case study for demonstrating the effectiveness of this framework.

Kolmogorov-Arnold Network for Online Reinforcement Learning

Authors: Victor Augusto Kich, Jair Augusto Bottega, Raul Steinmetz, Ricardo Bedin Grando, Ayano Yorozu, Akihisa Ohya

Venue: International Conference on Control, Automation and Systems

Citation Count: 5

Abstract: Kolmogorov-Arnold Networks (KANs) have shown potential as an alternative to Multi-Layer Perceptrons (MLPs) in neural networks, providing universal function approximation with fewer parameters and reduced memory usage. In this paper, we explore the use of KANs as function approximators within the Proximal Policy Optimization (PPO) algorithm. We evaluate this approach by comparing its performance to the original MLP-based PPO using the DeepMind Control Proprio Robotics benchmark. Our results indicate that the KAN-based reinforcement learning algorithm can achieve comparable performance to its MLP-based counterpart, often with fewer parameters. These findings suggest that KANs may offer a more efficient option for reinforcement learning models.

Physics-Informed Kolmogorov-Arnold Networks for Power System Dynamics

Authors: Hang Shuai, Fangxing Li

Venue: IEEE Open Access Journal of Power and Energy

Citation Count: 10

Abstract: This paper presents, for the first time, a framework for Kolmogorov-Arnold Networks (KANs) in power system applications. Inspired by the recently proposed KAN architecture, this paper proposes physics-informed Kolmogorov-Arnold Networks (PIKANs), a novel KAN-based physics-informed neural network (PINN) tailored to efficiently and accurately learn dynamics within power systems. The PIKANs present a promising alternative to conventional Multi-Layer Perceptrons (MLPs) based PINNs, achieving superior accuracy in predicting power system dynamics while employing a smaller network size. Simulation results on a single-machine infinite bus system and a 4-bus 2- generator system underscore the accuracy of the PIKANs in predicting rotor angle and frequency with fewer learnable parameters than conventional PINNs. Furthermore, the simulation results demonstrate PIKANs capability to accurately identify uncertain inertia and damping coefficients. This work opens up a range of opportunities for the application of KANs in power systems, enabling efficient determination of grid dynamics and precise parameter identification.

KAN You See It? KANs and Sentinel for Effective and Explainable Crop Field Segmentation

Authors: Daniele Rege Cambrin, Eleonora Poeta, Eliana Pastor, Tania Cerquitelli, Elena Baralis, Paolo Garza

Venue: ECCV Workshops

Citation Count: 9

Abstract: Segmentation of crop fields is essential for enhancing agricultural productivity, monitoring crop health, and promoting sustainable practices. Deep learning models adopted for this task must ensure accurate and reliable predictions to avoid economic losses and environmental impact. The newly proposed Kolmogorov-Arnold networks (KANs) offer promising advancements in the performance of neural networks. This paper analyzes the integration of KAN layers into the U-Net architecture (U-KAN) to segment crop fields using Sentinel-2 and Sentinel-1 satellite images and provides an analysis of the performance and explainability of these networks. Our findings indicate a 2\% improvement in IoU compared to the traditional full-convolutional U-Net model in fewer GFLOPs. Furthermore, gradient-based explanation techniques show that U-KAN predictions are highly plausible and that the network has a very high ability to focus on the boundaries of cultivated areas rather than on the areas themselves. The per-channel relevance analysis also reveals that some channels are irrelevant to this task.

VulCatch: Enhancing Binary Vulnerability Detection through CodeT5 Decompilation and KAN Advanced Feature Extraction

Authors: Abdulrahman Hamman Adama Chukkol, Senlin Luo, Kashif Sharif, Yunusa Haruna, Muhammad Muhammad Abdullahi

Citation Count: 1

Abstract: Binary program vulnerability detection is critical for software security, yet existing deep learning approaches often rely on source code analysis, limiting their ability to detect unknown vulnerabilities. To address this, we propose VulCatch, a binary-level vulnerability detection framework. VulCatch introduces a Synergy Decompilation Module (SDM) and Kolmogorov-Arnold Networks (KAN) to transform raw binary code into pseudocode using CodeT5, preserving high-level semantics for deep analysis with tools like Ghidra and IDA. KAN further enhances feature transformation, enabling the detection of complex vulnerabilities. VulCatch employs word2vec, Inception Blocks, BiLSTM Attention, and Residual connections to achieve high detection accuracy (98.88%) and precision (97.92%), while minimizing false positives (1.56%) and false negatives (2.71%) across seven CVE datasets.

Kolmogorov-Arnold Networks (KAN) for Time Series Classification and Robust Analysis

Authors: Chang Dong, Liangwei Zheng, Weitong Chen

Venue: International Conference on Advanced Data Mining and Applications

Citation Count: 15

Abstract: Kolmogorov-Arnold Networks (KAN) has recently attracted significant attention as a promising alternative to traditional Multi-Layer Perceptrons (MLP). Despite their theoretical appeal, KAN require validation on large-scale benchmark datasets. Time series data, which has become increasingly prevalent in recent years, especially univariate time series are naturally suited for validating KAN. Therefore, we conducted a fair comparison among KAN, MLP, and mixed structures. The results indicate that KAN can achieve performance comparable to, or even slightly better than, MLP across 128 time series datasets. We also performed an ablation study on KAN, revealing that the output is primarily determined by the base component instead of b-spline function. Furthermore, we assessed the robustness of these models and found that KAN and the hybrid structure MLP_KAN exhibit significant robustness advantages, attributed to their lower Lipschitz constants. This suggests that KAN and KAN layers hold strong potential to be robust models or to improve the adversarial robustness of other models.

KAN versus MLP on Irregular or Noisy Functions

Authors: Chen Zeng, Jiahui Wang, Haoran Shen, Qiao Wang

Citation Count: 9

Abstract: In this paper, we compare the performance of Kolmogorov-Arnold Networks (KAN) and Multi-Layer Perceptron (MLP) networks on irregular or noisy functions. We control the number of parameters and the size of the training samples to ensure a fair comparison. For clarity, we categorize the functions into six types: regular functions, continuous functions with local non-differentiable points, functions with jump discontinuities, functions with singularities, functions with coherent oscillations, and noisy functions. Our experimental results indicate that KAN does not always perform best. For some types of functions, MLP outperforms or performs comparably to KAN. Furthermore, increasing the size of training samples can improve performance to some extent. When noise is added to functions, the irregular features are often obscured by the noise, making it challenging for both MLP and KAN to extract these features effectively. We hope these experiments provide valuable insights for future neural network research and encourage further investigations to overcome these challenges.

The Dawn of KAN in Image-to-Image (I2I) Translation: Integrating Kolmogorov-Arnold Networks with GANs for Unpaired I2I Translation

Authors: Arpan Mahara, Naphtali D. Rishe, Liangdong Deng

Citation Count: 2

Abstract: Image-to-Image translation in Generative Artificial Intelligence (Generative AI) has been a central focus of research, with applications spanning healthcare, remote sensing, physics, chemistry, photography, and more. Among the numerous methodologies, Generative Adversarial Networks (GANs) with contrastive learning have been particularly successful. This study aims to demonstrate that the Kolmogorov-Arnold Network (KAN) can effectively replace the Multi-layer Perceptron (MLP) method in generative AI, particularly in the subdomain of image-to-image translation, to achieve better generative quality. Our novel approach replaces the two-layer MLP with a two-layer KAN in the existing Contrastive Unpaired Image-to-Image Translation (CUT) model, developing the KAN-CUT model. This substitution favors the generation of more informative features in low-dimensional vector representations, which contrastive learning can utilize more effectively to produce high-quality images in the target domain. Extensive experiments, detailed in the results section, demonstrate the applicability of KAN in conjunction with contrastive learning and GANs in Generative AI, particularly for image-to-image translation. This work suggests that KAN could be a valuable component in the broader generative AI domain.

A Conflicts-free, Speed-lossless KAN-based Reinforcement Learning Decision System for Interactive Driving in Roundabouts

Authors: Zhihao Lin, Zhen Tian, Jianglin Lan, Qi Zhang, Ziyang Ye, Hanyang Zhuang, Xianxian Zhao

Citation Count: 5

Abstract: Safety and efficiency are crucial for autonomous driving in roundabouts, especially mixed traffic with both autonomous vehicles (AVs) and human-driven vehicles. This paper presents a learning-based algorithm that promotes safe and efficient driving across varying roundabout traffic conditions. A deep Q-learning network is used to learn optimal strategies in complex multi-vehicle roundabout scenarios, while a Kolmogorov-Arnold Network (KAN) improves the AVs’ environmental understanding. To further enhance safety, an action inspector filters unsafe actions, and a route planner optimizes driving efficiency. Moreover, model predictive control ensures stability and precision in execution. Experimental results demonstrate that the proposed system consistently outperforms state-of-the-art methods, achieving fewer collisions, reduced travel time, and stable training with smooth reward convergence.

Activation Space Selectable Kolmogorov-Arnold Networks

Authors: Zhuoqin Yang, Jiansong Zhang, Xiaoling Luo, Zheng Lu, Linlin Shen

Citation Count: 5

Abstract: The multilayer perceptron (MLP), a fundamental paradigm in current artificial intelligence, is widely applied in fields such as computer vision and natural language processing. However, the recently proposed Kolmogorov-Arnold Network (KAN), based on nonlinear additive connections, has been proven to achieve performance comparable to MLPs with significantly fewer parameters. Despite this potential, the use of a single activation function space results in reduced performance of KAN and related works across different tasks. To address this issue, we propose an activation space Selectable KAN (S-KAN). S-KAN employs an adaptive strategy to choose the possible activation mode for data at each feedforward KAN node. Our approach outperforms baseline methods in seven representative function fitting tasks and significantly surpasses MLP methods with the same level of parameters. Furthermore, we extend the structure of S-KAN and propose an activation space selectable Convolutional KAN (S-ConvKAN), which achieves leading results on four general image classification datasets. Our method mitigates the performance variability of the original KAN across different tasks and demonstrates through extensive experiments that feedforward KANs with selectable activations can achieve or even exceed the performance of MLP-based methods. This work contributes to the understanding of the data-centric design of new AI paradigms and provides a foundational reference for innovations in KAN-based network architectures.

Photonic KAN: a Kolmogorov-Arnold network inspired efficient photonic neuromorphic architecture

Authors: Yiwei Peng, Sean Hooten, Xinling Yu, Thomas Van Vaerenbergh, Yuan Yuan, Xian Xiao, Bassem Tossoun, Stanley Cheung, Marco Fiorentino, Raymond Beausoleil

Citation Count: 1

Abstract: Kolmogorov-Arnold Networks (KAN) models were recently proposed and claimed to provide improved parameter scaling and interpretability compared to conventional multilayer perceptron (MLP) models. Inspired by the KAN architecture, we propose the Photonic KAN – an integrated all-optical neuromorphic platform leveraging highly parametric optical nonlinear transfer functions along KAN edges. In this work, we implement such nonlinearities in the form of cascaded ring-assisted Mach-Zehnder Interferometer (MZI) devices. This innovative design has the potential to address key limitations of current photonic neural networks. In our test cases, the Photonic KAN showcases enhanced parameter scaling and interpretability compared to existing photonic neural networks. The photonic KAN achieves approximately 65$\times$ reduction in energy consumption and area, alongside a 50$\times$ reduction in latency compared to previous MZI-based photonic accelerators with similar performance for function fitting task. This breakthrough presents a promising new avenue for expanding the scalability and efficiency of neuromorphic hardware platforms.

Beyond KAN: Introducing KarSein for Adaptive High-Order Feature Interaction Modeling in CTR Prediction

Authors: Yunxiao Shi, Wujiang Xu, Haimin Zhang, Qiang Wu, Min Xu

Citation Count: 1

Abstract: Modeling high-order feature interactions is crucial for click-through rate (CTR) prediction, yet traditional approaches typically predefine a maximum interaction order and exhaustively enumerate feature combinations up to that order. This paradigm depends heavily on prior domain knowledge to delimit the interaction space and incurs substantial computational overhead. As a result, conventional CTR models face a persistent tension between enriching representations with complex high-order interactions and keeping computation tractable. To address this dual challenge, this study introduces the Kolmogorov-Arnold Represented Sparse Efficient Interaction Network (KarSein). Drawing inspiration from the learnable activation mechanism in the Kolmogorov-Arnold Network (KAN), KarSein leverages this mechanism to adaptively transform low-order basic features into high-order feature interactions, offering a novel approach to feature interaction modeling. KarSein extends the capabilities of KAN by introducing a more efficient architecture that significantly reduces computational costs while accommodating two-dimensional embedding vectors as feature inputs. Furthermore, it overcomes the limitation of KAN’s its inability to spontaneously capture multiplicative relationships among features. Extensive experiments highlight the superiority of KarSein, demonstrating its ability to surpass not only the vanilla implementation of KAN in CTR prediction tasks but also other baseline methods. Remarkably, KarSein achieves exceptional predictive accuracy while maintaining a highly compact parameter size and minimal computational overhead. Moreover, KarSein exhibits strong interpretability and structural sparsity. As the first systematic adaptation of KAN to CTR prediction, KarSein offers a practical, parameter-efficient, and interpretable alternative for modeling complex feature interactions in CTR prediction.

FourierKAN outperforms MLP on Text Classification Head Fine-tuning

Authors: Abdullah Al Imran, Md Farhan Ishmam

Abstract: In resource constraint settings, adaptation to downstream classification tasks involves fine-tuning the final layer of a classifier (i.e. classification head) while keeping rest of the model weights frozen. Multi-Layer Perceptron (MLP) heads fine-tuned with pre-trained transformer backbones have long been the de facto standard for text classification head fine-tuning. However, the fixed non-linearity of MLPs often struggles to fully capture the nuances of contextual embeddings produced by pre-trained models, while also being computationally expensive. In our work, we investigate the efficacy of KAN and its variant, Fourier KAN (FR-KAN), as alternative text classification heads. Our experiments reveal that FR-KAN significantly outperforms MLPs with an average improvement of 10% in accuracy and 11% in F1-score across seven pre-trained transformer models and four text classification tasks. Beyond performance gains, FR-KAN is more computationally efficient and trains faster with fewer parameters. These results underscore the potential of FR-KAN to serve as a lightweight classification head, with broader implications for advancing other Natural Language Processing (NLP) tasks.

Detecting the Undetectable: Combining Kolmogorov-Arnold Networks and MLP for AI-Generated Image Detection

Authors: Taharim Rahman Anon, Jakaria Islam Emon

Citation Count: 4

Abstract: As artificial intelligence progresses, the task of distinguishing between real and AI-generated images is increasingly complicated by sophisticated generative models. This paper presents a novel detection framework adept at robustly identifying images produced by cutting-edge generative AI models, such as DALL-E 3, MidJourney, and Stable Diffusion 3. We introduce a comprehensive dataset, tailored to include images from these advanced generators, which serves as the foundation for extensive evaluation. we propose a classification system that integrates semantic image embeddings with a traditional Multilayer Perceptron (MLP). This baseline system is designed to effectively differentiate between real and AI-generated images under various challenging conditions. Enhancing this approach, we introduce a hybrid architecture that combines Kolmogorov-Arnold Networks (KAN) with the MLP. This hybrid model leverages the adaptive, high-resolution feature transformation capabilities of KAN, enabling our system to capture and analyze complex patterns in AI-generated images that are typically overlooked by conventional models. In out-of-distribution testing, our proposed model consistently outperformed the standard MLP across three out of distribution test datasets, demonstrating superior performance and robustness in classifying real images from AI-generated images with impressive F1 scores.

KAN 2.0: Kolmogorov-Arnold Networks Meet Science

Authors: Ziming Liu, Pingchuan Ma, Yixuan Wang, Wojciech Matusik, Max Tegmark

Citation Count: 70

Abstract: A major challenge of AI + Science lies in their inherent incompatibility: today’s AI is primarily based on connectionism, while science depends on symbolism. To bridge the two worlds, we propose a framework to seamlessly synergize Kolmogorov-Arnold Networks (KANs) and science. The framework highlights KANs’ usage for three aspects of scientific discovery: identifying relevant features, revealing modular structures, and discovering symbolic formulas. The synergy is bidirectional: science to KAN (incorporating scientific knowledge into KANs), and KAN to science (extracting scientific insights from KANs). We highlight major new functionalities in the pykan package: (1) MultKAN: KANs with multiplication nodes. (2) kanpiler: a KAN compiler that compiles symbolic formulas into KANs. (3) tree converter: convert KANs (or any neural networks) to tree graphs. Based on these tools, we demonstrate KANs’ capability to discover various types of physical laws, including conserved quantities, Lagrangians, symmetries, and constitutive laws.

Kolmogorov Arnold Networks in Fraud Detection: Bridging the Gap Between Theory and Practice

Authors: Yang Lu, Felix Zhan

Citation Count: 1

Abstract: This study evaluates the applicability of Kolmogorov-Arnold Networks (KAN) in fraud detection, finding that their effectiveness is context-dependent. We propose a quick decision rule using Principal Component Analysis (PCA) to assess the suitability of KAN: if data can be effectively separated in two dimensions using splines, KAN may outperform traditional models; otherwise, other methods could be more appropriate. We also introduce a heuristic approach to hyperparameter tuning, significantly reducing computational costs. These findings suggest that while KAN has potential, its use should be guided by data-specific assessments.

Deep-MacroFin: Informed Equilibrium Neural Network for Continuous Time Economic Models

Authors: Yuntao Wu, Jiayuan Guo, Goutham Gopalakrishna, Zissis Poulos

Abstract: In this paper, we present Deep-MacroFin, a comprehensive framework designed to solve partial differential equations, with a particular focus on models in continuous time economics. This framework leverages deep learning methodologies, including Multi-Layer Perceptrons and the newly developed Kolmogorov-Arnold Networks. It is optimized using economic information encapsulated by Hamilton-Jacobi-Bellman (HJB) equations and coupled algebraic equations. The application of neural networks holds the promise of accurately resolving high-dimensional problems with fewer computational demands and limitations compared to other numerical methods. This framework can be readily adapted for systems of partial differential equations in high dimensions. Importantly, it offers a more efficient (5$\times$ less CUDA memory and 40$\times$ fewer FLOPs in 100D problems) and user-friendly implementation than existing libraries. We also incorporate a time-stepping scheme to enhance training stability for nonlinear HJB equations, enabling the solution of 50D economic models.

Want to train KANS at scale? Now UKAN!

Authors: Alireza Moradzadeh, Srimukh Prasad Veccham, Lukasz Wawrzyniak, Miles Macklin, Saee G. Paliwal

Citation Count: 1

Abstract: Kolmogorov-Arnold Networks (KANs) have recently emerged as a powerful alternative to traditional multilayer perceptrons. However, their reliance on predefined, bounded grids restricts their ability to approximate functions on unbounded domains. To address this, we present Unbounded Kolmogorov-Arnold Networks (UKANs), a method that removes the need for bounded grids in traditional Kolmogorov-Arnold Networks (KANs). The key innovation of this method is a coefficient-generator (CG) model that produces, on the fly, only the B-spline coefficients required locally on an unbounded symmetric grid. UKANs couple multilayer perceptrons with KANs by feeding the positional encoding of grid groups into the CG model, enabling function approximation on unbounded domains without requiring data normalization. To reduce the computational cost of both UKANs and KANs, we introduce a GPU-accelerated library that lowers B-spline evaluation complexity by a factor proportional to the grid size, enabling large-scale learning by leveraging efficient memory management, in line with recent software advances such as FlashAttention and FlashFFTConv. Performance benchmarking confirms the superior memory and computational efficiency of our accelerated KAN (warpKAN), and UKANs, showing a 3-30x speed-up and up to 1000x memory reduction compared to vanilla KANs. Experiments on regression, classification, and generative tasks demonstrate the effectiveness of UKANs to match or surpass KAN accuracy. Finally, we use both accelerated KAN and UKAN in a molecular property prediction task, establishing the feasibility of large-scale end-to-end training with our optimized implementation.

Are KANs Effective for Multivariate Time Series Forecasting?

Authors: Xiao Han, Xinfeng Zhang, Yiling Wu, Zhenduo Zhang, Zhe Wu

Citation Count: 5

Abstract: Multivariate time series forecasting is a crucial task that predicts the future states based on historical inputs. Related techniques have been developing in parallel with the machine learning community, from early statistical learning methods to current deep learning methods. Despite their significant advancements, existing methods continue to struggle with the challenge of inadequate interpretability. The rise of the Kolmogorov-Arnold Network (KAN) provides a new perspective to solve this challenge, but current work has not yet concluded whether KAN is effective in time series forecasting tasks. In this paper, we aim to evaluate the effectiveness of KANs in time-series forecasting from the perspectives of performance, integrability, efficiency, and interpretability. To this end, we propose the Multi-layer Mixture-of-KAN network (MMK), which achieves excellent performance while retaining KAN’s ability to be transformed into a combination of symbolic functions. The core module of MMK is the mixture-of-KAN layer, which uses a mixture-of-experts structure to assign variables to best-matched KAN experts. Then, we explore some useful experimental strategies to deal with the issues in the training stage. Finally, we compare MMK and various baselines on seven datasets. Extensive experimental and visualization results demonstrate that KANs are effective in multivariate time series forecasting. Code is available at: https://github.com/2448845600/EasyTSF.

KonvLiNA: Integrating Kolmogorov-Arnold Network with Linear Nyström Attention for feature fusion in Crop Field Detection

Authors: Haruna Yunusa, Qin Shiyin, Adamu Lawan, Abdulrahman Hamman Adama Chukkol

Venue: International Conference on Machine Vision

Citation Count: 1

Abstract: Crop field detection is a critical component of precision agriculture, essential for optimizing resource allocation and enhancing agricultural productivity. This study introduces KonvLiNA, a novel framework that integrates Convolutional Kolmogorov-Arnold Networks (cKAN) with Nyström attention mechanisms for effective crop field detection. Leveraging KAN adaptive activation functions and the efficiency of Nyström attention in handling largescale data, KonvLiNA significantly enhances feature extraction, enabling the model to capture intricate patterns in complex agricultural environments. Experimental results on rice crop dataset demonstrate KonvLiNA superiority over state-of-the-art methods, achieving a 0.415 AP and 0.459 AR with the Swin-L backbone, outperforming traditional YOLOv8 by significant margins. Additionally, evaluation on the COCO dataset showcases competitive performance across small, medium, and large objects, highlighting KonvLiNA efficacy in diverse agricultural settings. This work highlights the potential of hybrid KAN and attention mechanisms for advancing precision agriculture through improved crop field detection and management.

On the Robustness of Kolmogorov-Arnold Networks: An Adversarial Perspective

Authors: Tal Alter, Raz Lapid, Moshe Sipper

Citation Count: 6

Abstract: Kolmogorov-Arnold Networks (KANs) have recently emerged as a novel approach to function approximation, demonstrating remarkable potential in various domains. Despite their theoretical promise, the robustness of KANs under adversarial conditions has yet to be thoroughly examined. In this paper we explore the adversarial robustness of KANs, with a particular focus on image classification tasks. We assess the performance of KANs against standard white box and black-box adversarial attacks, comparing their resilience to that of established neural network architectures. Our experimental evaluation encompasses a variety of standard image classification benchmark datasets and investigates both fully connected and convolutional neural network architectures, of three sizes: small, medium, and large. We conclude that small- and medium-sized KANs (either fully connected or convolutional) are not consistently more robust than their standard counterparts, but that large-sized KANs are, by and large, more robust. This comprehensive evaluation of KANs in adversarial scenarios offers the first in-depth analysis of KAN security, laying the groundwork for future research in this emerging field.

GINN-KAN: Interpretability pipelining with applications in Physics Informed Neural Networks

Authors: Nisal Ranasinghe, Yu Xia, Sachith Seneviratne, Saman Halgamuge

Citation Count: 4

Abstract: Neural networks are powerful function approximators, yet their ``black-box” nature often renders them opaque and difficult to interpret. While many post-hoc explanation methods exist, they typically fail to capture the underlying reasoning processes of the networks. A truly interpretable neural network would be trained similarly to conventional models using techniques such as backpropagation, but additionally provide insights into the learned input-output relationships. In this work, we introduce the concept of interpretability pipelineing, to incorporate multiple interpretability techniques to outperform each individual technique. To this end, we first evaluate several architectures that promise such interpretability, with a particular focus on two recent models selected for their potential to incorporate interpretability into standard neural network architectures while still leveraging backpropagation: the Growing Interpretable Neural Network (GINN) and Kolmogorov Arnold Networks (KAN). We analyze the limitations and strengths of each and introduce a novel interpretable neural network GINN-KAN that synthesizes the advantages of both models. When tested on the Feynman symbolic regression benchmark datasets, GINN-KAN outperforms both GINN and KAN. To highlight the capabilities and the generalizability of this approach, we position GINN-KAN as an alternative to conventional black-box networks in Physics-Informed Neural Networks (PINNs). We expect this to have far-reaching implications in the application of deep learning pipelines in the natural sciences. Our experiments with this interpretable PINN on 15 different partial differential equations demonstrate that GINN-KAN augmented PINNs outperform PINNs with black-box networks in solving differential equations and surpass the capabilities of both GINN and KAN.

DualKanbaFormer: An Efficient Selective Sparse Framework for Multimodal Aspect-based Sentiment Analysis

Authors: Adamu Lawan, Juhua Pu, Haruna Yunusa, Muhammad Lawan, Aliyu Umar, Adamu Sani Yahya, Mahmoud Basi

Abstract: Multimodal Aspect-based Sentiment Analysis (MABSA) enhances sentiment detection by integrating textual data with complementary modalities, such as images, to provide a more refined and comprehensive understanding of sentiment. However, conventional attention mechanisms, despite notable benchmarks, are hindered by quadratic complexity, limiting their ability to fully capture global contextual dependencies and rich semantic information in both modalities. To address this limitation, we introduce DualKanbaFormer, a novel framework that leverages parallel Textual and Visual KanbaFormer modules for robust multimodal analysis. Our approach incorporates Aspect-Driven Sparse Attention (ADSA) to dynamically balance coarse-grained aggregation and fine-grained selection for aspect-focused precision, ensuring the preservation of both global context awareness and local precision in textual and visual representations. Additionally, we utilize the Selective State Space Model (Mamba) to capture extensive global semantic information across both modalities. Furthermore, We replace traditional feed-forward networks and normalization with Kolmogorov-Arnold Networks (KANs) and Dynamic Tanh (DyT) to enhance non-linear expressivity and inference stability. To facilitate the effective integration of textual and visual features, we design a multimodal gated fusion layer that dynamically optimizes inter-modality interactions, significantly enhancing the models efficacy in MABSA tasks. Comprehensive experiments on two publicly available datasets reveal that DualKanbaFormer consistently outperforms several state-of-the-art (SOTA) models.

Enhancing Intrusion Detection in IoT Environments: An Advanced Ensemble Approach Using Kolmogorov-Arnold Networks

Authors: Amar Amouri, Mohamad Mahmoud Al Rahhal, Yakoub Bazi, Ismail Butun, Imad Mahgoub

Venue: International Symposium on Networks, Computers and Communications

Citation Count: 3

Abstract: In recent years, the evolution of machine learning techniques has significantly impacted the field of intrusion detection, particularly within the context of the Internet of Things (IoT). As IoT networks expand, the need for robust security measures to counteract potential threats has become increasingly critical. This paper introduces a hybrid Intrusion Detection System (IDS) that synergistically combines Kolmogorov-Arnold Networks (KANs) with the XGBoost algorithm. Our proposed IDS leverages the unique capabilities of KANs, which utilize learnable activation functions to model complex relationships within data, alongside the powerful ensemble learning techniques of XGBoost, known for its high performance in classification tasks. This hybrid approach not only enhances the detection accuracy but also improves the interpretability of the model, making it suitable for dynamic and intricate IoT environments. Experimental evaluations demonstrate that our hybrid IDS achieves an impressive detection accuracy exceeding 99% in distinguishing between benign and malicious activities. Additionally, we were able to achieve F1 scores, precision, and recall that exceeded 98%. Furthermore, we conduct a comparative analysis against traditional Multi-Layer Perceptron (MLP) networks, assessing performance metrics such as Precision, Recall, and F1-score. The results underscore the efficacy of integrating KANs with XGBoost, highlighting the potential of this innovative approach to significantly strengthen the security framework of IoT networks.

Addressing common misinterpretations of KART and UAT in neural network literature

Author: Vugar Ismailov

Citation Count: 1

Abstract: This note addresses the Kolmogorov-Arnold Representation Theorem (KART) and the Universal Approximation Theorem (UAT), focusing on their frequent misinterpretations found in the neural network literature. Our remarks aim to support a more accurate understanding of KART and UAT among neural network specialists. In addition, we explore the minimal number of neurons required for universal approximation, showing that the same number of neurons needed for exact representation of functions in KART-based networks also suffices for standard multilayer perceptrons in the context of approximation.

LAR-IQA: A Lightweight, Accurate, and Robust No-Reference Image Quality Assessment Model

Authors: Nasim Jamshidi Avanaki, Abhijay Ghildyal, Nabajeet Barman, Saman Zadtootaghaj

Venue: ECCV Workshops

Citation Count: 1

Abstract: Recent advancements in the field of No-Reference Image Quality Assessment (NR-IQA) using deep learning techniques demonstrate high performance across multiple open-source datasets. However, such models are typically very large and complex making them not so suitable for real-world deployment, especially on resource- and battery-constrained mobile devices. To address this limitation, we propose a compact, lightweight NR-IQA model that achieves state-of-the-art (SOTA) performance on ECCV AIM UHD-IQA challenge validation and test datasets while being also nearly 5.7 times faster than the fastest SOTA model. Our model features a dual-branch architecture, with each branch separately trained on synthetically and authentically distorted images which enhances the model’s generalizability across different distortion types. To improve robustness under diverse real-world visual conditions, we additionally incorporate multiple color spaces during the training process. We also demonstrate the higher accuracy of recently proposed Kolmogorov-Arnold Networks (KANs) for final quality regression as compared to the conventional Multi-Layer Perceptrons (MLPs). Our evaluation considering various open-source datasets highlights the practical, high-accuracy, and robust performance of our proposed lightweight model. Code: https://github.com/nasimjamshidi/LAR-IQA.

AASIST3: KAN-Enhanced AASIST Speech Deepfake Detection using SSL Features and Additional Regularization for the ASVspoof 2024 Challenge

Authors: Kirill Borodin, Vasiliy Kudryavtsev, Dmitrii Korzh, Alexey Efimenko, Grach Mkrtchian, Mikhail Gorodnichev, Oleg Y. Rogov

Venue: The Automatic Speaker Verification Spoofing Countermeasures Workshop (ASVspoof 2024)

Citation Count: 3

Abstract: Automatic Speaker Verification (ASV) systems, which identify speakers based on their voice characteristics, have numerous applications, such as user authentication in financial transactions, exclusive access control in smart devices, and forensic fraud detection. However, the advancement of deep learning algorithms has enabled the generation of synthetic audio through Text-to-Speech (TTS) and Voice Conversion (VC) systems, exposing ASV systems to potential vulnerabilities. To counteract this, we propose a novel architecture named AASIST3. By enhancing the existing AASIST framework with Kolmogorov-Arnold networks, additional layers, encoders, and pre-emphasis techniques, AASIST3 achieves a more than twofold improvement in performance. It demonstrates minDCF results of 0.5357 in the closed condition and 0.1414 in the open condition, significantly enhancing the detection of synthetic voices and improving ASV security. \textbf{The new version of the model is publicly available at \href{https://huggingface.co/lab260/Spectra-AASIST3}{\underline{HuggingFace (2026)}}}

September

GNN-Empowered Effective Partial Observation MARL Method for AoI Management in Multi-UAV Network

Authors: Yuhao Pan, Xiucheng Wang, Zhiyao Xu, Nan Cheng, Wenchao Xu, Jun-jie Zhang

Venue: IEEE Internet of Things Journal

Citation Count: 4

Abstract: Unmanned Aerial Vehicles (UAVs), due to their low cost and high flexibility, have been widely used in various scenarios to enhance network performance. However, the optimization of UAV trajectories in unknown areas or areas without sufficient prior information, still faces challenges related to poor planning performance and low distributed execution. These challenges arise when UAVs rely solely on their own observation information and the information from other UAVs within their communicable range, without access to global information. To address these challenges, this paper proposes the Qedgix framework, which combines graph neural networks (GNNs) and the QMIX algorithm to achieve distributed optimization of the Age of Information (AoI) for users in unknown scenarios. The framework utilizes GNNs to extract information from UAVs, users within the observable range, and other UAVs within the communicable range, thereby enabling effective UAV trajectory planning. Due to the discretization and temporal features of AoI indicators, the Qedgix framework employs QMIX to optimize distributed partially observable Markov decision processes (Dec-POMDP) based on centralized training and distributed execution (CTDE) with respect to mean AoI values of users. By modeling the UAV network optimization problem in terms of AoI and applying the Kolmogorov-Arnold representation theorem, the Qedgix framework achieves efficient neural network training through parameter sharing based on permutation invariance. Simulation results demonstrate that the proposed algorithm significantly improves convergence speed while reducing the mean AoI values of users. The code is available at https://github.com/UNIC-Lab/Qedgix.

Application of Kolmogorov-Arnold Networks in high energy physics

Authors: E. Abasov, P. Volkov, G. Vorotnikov, L. Dudko, A. Zaborenko, E. Iudin, A. Markina, M. Perfilov

Venue: Moscow University Physics Bulletin

Citation Count: 3

Abstract: Kolmogorov-Arnold Networks represent a recent advancement in machine learning, with the potential to outperform traditional perceptron-based neural networks across various domains as well as provide more interpretability with the use of symbolic formulas and pruning. This study explores the application of KANs to specific tasks in high-energy physics. We evaluate the performance of KANs in distinguishing multijet processes in proton-proton collisions and in reconstructing missing transverse momentum in events involving dark matter.

FC-KAN: Function Combinations in Kolmogorov-Arnold Networks

Authors: Hoang-Thang Ta, Duy-Quy Thai, Abu Bakar Siddiqur Rahman, Grigori Sidorov, Alexander Gelbukh

Citation Count: 8

Abstract: In this paper, we introduce FC-KAN, a Kolmogorov-Arnold Network (KAN) that leverages combinations of popular mathematical functions such as B-splines, wavelets, and radial basis functions on low-dimensional data through element-wise operations. We explore several methods for combining the outputs of these functions, including sum, element-wise product, the addition of sum and element-wise product, representations of quadratic and cubic functions, concatenation, linear transformation of the concatenated output, and others. In our experiments, we compare FC-KAN with a multi-layer perceptron network (MLP) and other existing KANs, such as BSRBF-KAN, EfficientKAN, FastKAN, and FasterKAN, on the MNIST and Fashion-MNIST datasets. Two variants of FC-KAN, which use a combination of outputs from B-splines and Derivative of Gaussians (DoG) and from B-splines and linear transformations in the form of a quadratic function, outperformed overall other models on the average of 5 independent training runs. We expect that FC-KAN can leverage function combinations to design future KANs. Our repository is publicly available at: https://github.com/hoangthangta/FC_KAN.

KAN See In the Dark

Authors: Aoxiang Ning, Minglong Xue, Jinhong He, Chengyun Song

Venue: IEEE Signal Processing Letters

Citation Count: 2

Abstract: Existing low-light image enhancement methods are difficult to fit the complex nonlinear relationship between normal and low-light images due to uneven illumination and noise effects. The recently proposed Kolmogorov-Arnold networks (KANs) feature spline-based convolutional layers and learnable activation functions, which can effectively capture nonlinear dependencies. In this paper, we design a KAN-Block based on KANs and innovatively apply it to low-light image enhancement. This method effectively alleviates the limitations of current methods constrained by linear network structures and lack of interpretability, further demonstrating the potential of KANs in low-level vision tasks. Given the poor perception of current low-light image enhancement methods and the stochastic nature of the inverse diffusion process, we further introduce frequency-domain perception for visually oriented enhancement. Extensive experiments demonstrate the competitive performance of our method on benchmark datasets. The code will be available at: https://github.com/AXNing/KSID}{https://github.com/AXNing/KSID.

Efficient prediction of potential energy surface and physical properties with Kolmogorov-Arnold Networks

Authors: Rui Wang, Hongyu Yu, Yang Zhong, Hongjun Xiang

Venue: Journal of Materials Informatics

Abstract: The application of machine learning methodologies for predicting properties within materials science has garnered significant attention. Among recent advancements, Kolmogorov-Arnold Networks (KANs) have emerged as a promising alternative to traditional Multi-Layer Perceptrons (MLPs). This study evaluates the impact of substituting MLPs with KANs within three established machine learning frameworks: Allegro, Neural Equivariant Interatomic Potentials (NequIP), and the Edge-Based Tensor Prediction Graph Neural Network (ETGNN). Our results demonstrate that the integration of KANs generally yields enhanced prediction accuracies. Specifically, replacing MLPs with KANs in the output blocks leads to notable improvements in accuracy and, in certain scenarios, also results in reduced training times. Furthermore, employing KANs exclusively in the output block facilitates faster inference and improved computational efficiency relative to utilizing KANs throughout the entire model. The selection of an optimal basis function for KANs is found to be contingent upon the particular problem at hand. Our results demonstrate the strong potential of KANs in enhancing machine learning potentials and material property predictions.

CoxKAN: Kolmogorov-Arnold Networks for Interpretable, High-Performance Survival Analysis

Authors: William Knottenbelt, William McGough, Rebecca Wray, Woody Zhidong Zhang, Jiashuai Liu, Ines Prata Machado, Zeyu Gao, Mireia Crispin-Ortuzar

Citation Count: 10

Abstract: Motivation: Survival analysis is a branch of statistics that is crucial in medicine for modeling the time to critical events such as death or relapse, in order to improve treatment strategies and patient outcomes. Selecting survival models often involves a trade-off between performance and interpretability; deep learning models offer high performance but lack the transparency of more traditional approaches. This poses a significant issue in medicine, where practitioners are reluctant to use black-box models for critical patient decisions. Results: We introduce CoxKAN, a Cox proportional hazards Kolmogorov-Arnold Network for interpretable, high-performance survival analysis. Kolmogorov-Arnold Networks (KANs) were recently proposed as an interpretable and accurate alternative to multi-layer perceptrons. We evaluated CoxKAN on four synthetic and nine real datasets, including five cohorts with clinical data and four with genomics biomarkers. In synthetic experiments, CoxKAN accurately recovered interpretable hazard function formulae and excelled in automatic feature selection. Evaluations on real datasets showed that CoxKAN consistently outperformed the traditional Cox proportional hazards model (by up to 4% in C-index) and matched or surpassed the performance of deep learning-based models. Importantly, CoxKAN revealed complex interactions between predictor variables and uncovered symbolic formulae, which are key capabilities that other survival analysis methods lack, to provide clear insights into the impact of key biomarkers on patient risk. Availability and implementation: CoxKAN is available at GitHub and Zenodo

CF-KAN: Kolmogorov-Arnold Network-based Collaborative Filtering to Mitigate Catastrophic Forgetting in Recommender Systems

Authors: Jin-Duk Park, Kyung-Min Kim, Won-Yong Shin

Citation Count: 3

Abstract: Collaborative filtering (CF) remains essential in recommender systems, leveraging user–item interactions to provide personalized recommendations. Meanwhile, a number of CF techniques have evolved into sophisticated model architectures based on multi-layer perceptrons (MLPs). However, MLPs often suffer from catastrophic forgetting, and thus lose previously acquired knowledge when new information is learned, particularly in dynamic environments requiring continual learning. To tackle this problem, we propose CF-KAN, a new CF method utilizing Kolmogorov-Arnold networks (KANs). By learning nonlinear functions on the edge level, KANs are more robust to the catastrophic forgetting problem than MLPs. Built upon a KAN-based autoencoder, CF-KAN is designed in the sense of effectively capturing the intricacies of sparse user–item interactions and retaining information from previous data instances. Despite its simplicity, our extensive experiments demonstrate 1) CF-KAN’s superiority over state-of-the-art methods in recommendation accuracy, 2) CF-KAN’s resilience to catastrophic forgetting, underscoring its effectiveness in both static and dynamic recommendation scenarios, and 3) CF-KAN’s edge-level interpretation facilitating the explainability of recommendations.

Self-Supervised State Space Model for Real-Time Traffic Accident Prediction Using eKAN Networks

Authors: Xin Tan, Meng Zhao

Abstract: Accurate prediction of traffic accidents across different times and regions is vital for public safety. However, existing methods face two key challenges: 1) Generalization: Current models rely heavily on manually constructed multi-view structures, like POI distributions and road network densities, which are labor-intensive and difficult to scale across cities. 2) Real-Time Performance: While some methods improve accuracy with complex architectures, they often incur high computational costs, limiting their real-time applicability. To address these challenges, we propose SSL-eKamba, an efficient self-supervised framework for traffic accident prediction. To enhance generalization, we design two self-supervised auxiliary tasks that adaptively improve traffic pattern representation through spatiotemporal discrepancy awareness. For real-time performance, we introduce eKamba, an efficient model that redesigns the Kolmogorov-Arnold Network (KAN) architecture. This involves using learnable univariate functions for input activation and applying a selective mechanism (Selective SSM) to capture multi-variate correlations, thereby improving computational efficiency. Extensive experiments on two real-world datasets demonstrate that SSL-eKamba consistently outperforms state-of-the-art baselines. This framework may also offer new insights for other spatiotemporal tasks. Our source code is publicly available at http://github.com/KevinT618/SSL-eKamba.

A Comprehensive Comparison Between ANNs and KANs For Classifying EEG Alzheimer’s Data

Authors: Akshay Sunkara, Sriram Sattiraju, Aakarshan Kumar, Zaryab Kanjiani, Himesh Anumala

Venue: 2024 IEEE MIT Undergraduate Research Technology Conference (URTC)

Citation Count: 1

Abstract: Alzheimer’s Disease is an incurable cognitive condition that affects thousands of people globally. While some diagnostic methods exist for Alzheimer’s Disease, many of these methods cannot detect Alzheimer’s in its earlier stages. Recently, researchers have explored the use of Electroencephalogram (EEG) technology for diagnosing Alzheimer’s. EEG is a noninvasive method of recording the brain’s electrical signals, and EEG data has shown distinct differences between patients with and without Alzheimer’s. In the past, Artificial Neural Networks (ANNs) have been used to predict Alzheimer’s from EEG data, but these models sometimes produce false positive diagnoses. This study aims to compare losses between ANNs and Kolmogorov-Arnold Networks (KANs) across multiple types of epochs, learning rates, and nodes. The results show that across these different parameters, ANNs are more accurate in predicting Alzheimer’s Disease from EEG signals.

KANtrol: A Physics-Informed Kolmogorov-Arnold Network Framework for Solving Multi-Dimensional and Fractional Optimal Control Problems

Author: Alireza Afzal Aghaei

Citation Count: 2

Abstract: In this paper, we introduce the KANtrol framework, which utilizes Kolmogorov-Arnold Networks (KANs) to solve optimal control problems involving continuous time variables. We explain how Gaussian quadrature can be employed to approximate the integral parts within the problem, particularly for integro-differential state equations. We also demonstrate how automatic differentiation is utilized to compute exact derivatives for integer-order dynamics, while for fractional derivatives of non-integer order, we employ matrix-vector product discretization within the KAN framework. We tackle multi-dimensional problems, including the optimal control of a 2D heat partial differential equation. The results of our simulations, which cover both forward and parameter identification problems, show that the KANtrol framework outperforms classical MLPs in terms of accuracy and efficiency.

HSR-KAN: Efficient Hyperspectral Image Super-Resolution via Kolmogorov-Arnold Networks

Authors: Baisong Li, Xingwang Wang, Haixiao Xu

Citation Count: 1

Abstract: Hyperspectral images (HSIs) have great potential in various visual tasks due to their rich spectral information. However, obtaining high-resolution hyperspectral images remains challenging due to limitations of physical imaging. Inspired by Kolmogorov-Arnold Networks (KANs), we propose an efficient HSI super-resolution (HSI-SR) model to fuse a low-resolution HSI (LR-HSI) and a high-resolution multispectral image (HR-MSI), yielding a high-resolution HSI (HR-HSI). To achieve the effective integration of spatial information from HR-MSI, we design a fusion module based on KANs, called KAN-Fusion. Further inspired by the channel attention mechanism, we design a spectral channel attention module called KAN Channel Attention Block (KAN-CAB) for post-fusion feature extraction. As a channel attention module integrated with KANs, KAN-CAB not only enhances the fine-grained adjustment ability of deep networks, enabling networks to accurately simulate details of spectral sequences and spatial textures, but also effectively avoid Curse of Dimensionality. Extensive experiments show that, compared to current state-of-the-art HSI-SR methods, proposed HSR-KAN achieves the best performance in terms of both qualitative and quantitative assessments. Our code is available at: https://github.com/Baisonm-Li/HSR-KAN.

MLP, XGBoost, KAN, TDNN, and LSTM-GRU Hybrid RNN with Attention for SPX and NDX European Call Option Pricing

Authors: Boris Ter-Avanesov, Homayoon Beigi

Abstract: We explore the performance of various artificial neural network architectures, including a multilayer perceptron (MLP), Kolmogorov-Arnold network (KAN), LSTM-GRU hybrid recursive neural network (RNN) models, and a time-delay neural network (TDNN) for pricing European call options. In this study, we attempt to leverage the ability of supervised learning methods, such as ANNs, KANs, and gradient-boosted decision trees, to approximate complex multivariate functions in order to calibrate option prices based on past market data. The motivation for using ANNs and KANs is the Universal Approximation Theorem and Kolmogorov-Arnold Representation Theorem, respectively. Specifically, we use S\&P 500 (SPX) and NASDAQ 100 (NDX) index options traded during 2015-2023 with times to maturity ranging from 15 days to over 4 years (OptionMetrics IvyDB US dataset). Black \& Scholes’s (BS) PDE \cite{Black1973} model’s performance in pricing the same options compared to real data is used as a benchmark. This model relies on strong assumptions, and it has been observed and discussed in the literature that real data does not match its predictions. Supervised learning methods are widely used as an alternative for calibrating option prices due to some of the limitations of this model. In our experiments, the BS model underperforms compared to all of the others. Also, the best TDNN model outperforms the best MLP model on all error metrics. We implement a simple self-attention mechanism to enhance the RNN models, significantly improving their performance. The best-performing model overall is the LSTM-GRU hybrid RNN model with attention. Also, the KAN model outperforms the TDNN and MLP models. We analyze the performance of all models by ticker, moneyness category, and over/under/correctly-priced percentage.

Efficient Privacy-Preserving KAN Inference Using Homomorphic Encryption

Authors: Zhizheng Lai, Yufei Zhou, Peijia Zheng, Lin Chen

Abstract: The recently proposed Kolmogorov-Arnold Networks (KANs) offer enhanced interpretability and greater model expressiveness. However, KANs also present challenges related to privacy leakage during inference. Homomorphic encryption (HE) facilitates privacy-preserving inference for deep learning models, enabling resource-limited users to benefit from deep learning services while ensuring data security. Yet, the complex structure of KANs, incorporating nonlinear elements like the SiLU activation function and B-spline functions, renders existing privacy-preserving inference techniques inadequate. To address this issue, we propose an accurate and efficient privacy-preserving inference scheme tailored for KANs. Our approach introduces a task-specific polynomial approximation for the SiLU activation function, dynamically adjusting the approximation range to ensure high accuracy on real-world datasets. Additionally, we develop an efficient method for computing B-spline functions within the HE domain, leveraging techniques such as repeat packing, lazy combination, and comparison functions. We evaluate the effectiveness of our privacy-preserving KAN inference scheme on both symbolic formula evaluation and image classification. The experimental results show that our model achieves accuracy comparable to plaintext KANs across various datasets and outperforms plaintext MLPs. Additionally, on the CIFAR-10 dataset, our inference latency achieves over 7 times speedup compared to the naive method.

Exploring Kolmogorov-Arnold networks for realistic image sharpness assessment

Authors: Shaode Yu, Ze Chen, Zhimu Yang, Jiacheng Gu, Bizu Feng

Venue: IEEE International Conference on Acoustics, Speech, and Signal Processing

Citation Count: 5

Abstract: Score prediction is crucial in evaluating realistic image sharpness based on collected informative features. Recently, Kolmogorov-Arnold networks (KANs) have been developed and witnessed remarkable success in data fitting. This study introduces the Taylor series-based KAN (TaylorKAN). Then, different KANs are explored in four realistic image databases (BID2011, CID2013, CLIVE, and KonIQ-10k) to predict the scores by using 15 mid-level features and 2048 high-level features. Compared to support vector regression, results show that KANs are generally competitive or superior, and TaylorKAN is the best one when mid-level features are used. This is the first study to investigate KANs on image quality assessment that sheds some light on how to select and further improve KANs in related tasks.

Reimagining Linear Probing: Kolmogorov-Arnold Networks in Transfer Learning

Authors: Sheng Shen, Rabih Younes

Citation Count: 1

Abstract: This paper introduces Kolmogorov-Arnold Networks (KAN) as an enhancement to the traditional linear probing method in transfer learning. Linear probing, often applied to the final layer of pre-trained models, is limited by its inability to model complex relationships in data. To address this, we propose substituting the linear probing layer with KAN, which leverages spline-based representations to approximate intricate functions. In this study, we integrate KAN with a ResNet-50 model pre-trained on ImageNet and evaluate its performance on the CIFAR-10 dataset. We perform a systematic hyperparameter search, focusing on grid size and spline degree (k), to optimize KAN’s flexibility and accuracy. Our results demonstrate that KAN consistently outperforms traditional linear probing, achieving significant improvements in accuracy and generalization across a range of configurations. These findings indicate that KAN offers a more powerful and adaptable alternative to conventional linear probing techniques in transfer learning.

A Glass-Box Deep-Learning Method for Electrical Energy System Modeling Based on Kolmogorov-Arnold Network

Authors: Zhenghao Zhou, Yiyan Li, Zelin Guo, Zheng Yan, Mo-Yuen Chow

Abstract: Deep learning methods have been widely used as an end-to-end modeling strategy of electrical energy systems because of their conveniency and powerful pattern recognition capability. However, due to the “closed-box” nature, deep learning methods have long been blamed for their poor interpretability when modeling a physical system. In this paper, we introduce a novel neural network structure, Kolmogorov-Arnold Network (KAN), to achieve “glass-box” modeling for electrical energy systems to enhance the interpretability. The most distinct feature of KAN lies in the learnable activation function together with the sparse training and symbolification process. Consequently, KAN can express the physical process with concise and explicit mathematical formulas while remaining the nonlinear-fitting capability of deep neural networks. Simulation results based on three electrical energy systems demonstrate the effectiveness of KAN in the aspects of interpretability, accuracy, robustness and generalization ability.

Effective Integration of KAN for Keyword Spotting

Authors: Anfeng Xu, Biqiao Zhang, Shuyu Kong, Yiteng Huang, Zhaojun Yang, Sangeeta Srivastava, Ming Sun

Venue: IEEE International Conference on Acoustics, Speech, and Signal Processing

Citation Count: 5

Abstract: Keyword spotting (KWS) is an important speech processing component for smart devices with voice assistance capability. In this paper, we investigate if Kolmogorov-Arnold Networks (KAN) can be used to enhance the performance of KWS. We explore various approaches to integrate KAN for a model architecture based on 1D Convolutional Neural Networks (CNN). We find that KAN is effective at modeling high-level features in lower-dimensional spaces, resulting in improved KWS performance when integrated appropriately. The findings shed light on understanding KAN for speech processing tasks and on other modalities for future researchers.

TabKANet: Tabular Data Modeling with Kolmogorov-Arnold Network and Transformer

Authors: Weihao Gao, Zheng Gong, Zhuo Deng, Fuju Rong, Chucheng Chen, Lan Ma

Citation Count: 5

Abstract: Tabular data is the most common type of data in real-life scenarios. In this study, we propose the TabKANet model for tabular data modeling, which targets the bottlenecks in learning from numerical content. We constructed a Kolmogorov-Arnold Network (KAN) based Numerical Embedding Module and unified numerical and categorical features encoding within a Transformer architecture. TabKANet has demonstrated stable and significantly superior performance compared to Neural Networks (NNs) across multiple public datasets in binary classification, multi-class classification, and regression tasks. Its performance is comparable to or surpasses that of Gradient Boosted Decision Tree models (GBDTs). Our code is publicly available on GitHub: https://github.com/AI-thpremed/TabKANet.

Can Kans (re)discover predictive models for Direct-Drive Laser Fusion?

Authors: Rahman Ejaz, Varchas Gopalaswamy, Riccardo Betti, Aarne Lees, Christopher Kanan

Abstract: The domain of laser fusion presents a unique and challenging predictive modeling application landscape for machine learning methods due to high problem complexity and limited training data. Data-driven approaches utilizing prescribed functional forms, inductive biases and physics-informed learning (PIL) schemes have been successful in the past for achieving desired generalization ability and model interpretation that aligns with physics expectations. In complex multi-physics application domains, however, it is not always obvious how architectural biases or discriminative penalties can be formulated. In this work, focusing on nuclear fusion energy using high powered lasers, we present the use of Kolmogorov-Arnold Networks (KANs) as an alternative to PIL for developing a new type of data-driven predictive model which is able to achieve high prediction accuracy and physics interpretability. A KAN based model, a MLP with PIL, and a baseline MLP model are compared in generalization ability and interpretation with a domain expert-derived symbolic regression model. Through empirical studies in this high physics complexity domain, we show that KANs can potentially provide benefits when developing predictive models for data-starved physics applications.

Implicit Neural Representations with Fourier Kolmogorov-Arnold Networks

Authors: Ali Mehrabian, Parsa Mojarad Adi, Moein Heidari, Ilker Hacihaliloglu

Venue: IEEE International Conference on Acoustics, Speech, and Signal Processing

Citation Count: 3

Abstract: Implicit neural representations (INRs) use neural networks to provide continuous and resolution-independent representations of complex signals with a small number of parameters. However, existing INR models often fail to capture important frequency components specific to each task. To address this issue, in this paper, we propose a Fourier Kolmogorov Arnold network (FKAN) for INRs. The proposed FKAN utilizes learnable activation functions modeled as Fourier series in the first layer to effectively control and learn the task-specific frequency components. In addition, the activation functions with learnable Fourier coefficients improve the ability of the network to capture complex patterns and details, which is beneficial for high-resolution and high-dimensional data. Experimental results show that our proposed FKAN model outperforms three state-of-the-art baseline schemes, and improves the peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) for the image representation task and intersection over union (IoU) for the 3D occupancy volume representation task, respectively. The code is available at github.com/Ali-Meh619/FKAN.

KAN-HyperpointNet for Point Cloud Sequence-Based 3D Human Action Recognition

Authors: Zhaoyu Chen, Xing Li, Qian Huang, Qiang Geng, Tianjin Yang, Shihao Han

Venue: IEEE International Conference on Acoustics, Speech, and Signal Processing

Abstract: Point cloud sequence-based 3D action recognition has achieved impressive performance and efficiency. However, existing point cloud sequence modeling methods cannot adequately balance the precision of limb micro-movements with the integrity of posture macro-structure, leading to the loss of crucial information cues in action inference. To overcome this limitation, we introduce D-Hyperpoint, a novel data type generated through a D-Hyperpoint Embedding module. D-Hyperpoint encapsulates both regional-momentary motion and global-static posture, effectively summarizing the unit human action at each moment. In addition, we present a D-Hyperpoint KANsMixer module, which is recursively applied to nested groupings of D-Hyperpoints to learn the action discrimination information and creatively integrates Kolmogorov-Arnold Networks (KAN) to enhance spatio-temporal interaction within D-Hyperpoints. Finally, we propose KAN-HyperpointNet, a spatio-temporal decoupled network architecture for 3D action recognition. Extensive experiments on two public datasets: MSR Action3D and NTU-RGB+D 60, demonstrate the state-of-the-art performance of our method.

KAN v.s. MLP for Offline Reinforcement Learning

Authors: Haihong Guo, Fengxin Li, Jiao Li, Hongyan Liu

Venue: IEEE International Conference on Acoustics, Speech, and Signal Processing

Abstract: Kolmogorov-Arnold Networks (KAN) is an emerging neural network architecture in machine learning. It has greatly interested the research community about whether KAN can be a promising alternative of the commonly used Multi-Layer Perceptions (MLP). Experiments in various fields demonstrated that KAN-based machine learning can achieve comparable if not better performance than MLP-based methods, but with much smaller parameter scales and are more explainable. In this paper, we explore the incorporation of KAN into the actor and critic networks for offline reinforcement learning (RL). We evaluated the performance, parameter scales, and training efficiency of various KAN and MLP based conservative Q-learning (CQL) on the the classical D4RL benchmark for offline RL. Our study demonstrates that KAN can achieve performance close to the commonly used MLP with significantly fewer parameters. This provides us an option to choose the base networks according to the requirements of the offline RL tasks.

Kolmogorov-Arnold Networks in Low-Data Regimes: A Comparative Study with Multilayer Perceptrons

Author: Farhad Pourkamali-Anaraki

Citation Count: 5

Abstract: Multilayer Perceptrons (MLPs) have long been a cornerstone in deep learning, known for their capacity to model complex relationships. Recently, Kolmogorov-Arnold Networks (KANs) have emerged as a compelling alternative, utilizing highly flexible learnable activation functions directly on network edges, a departure from the neuron-centric approach of MLPs. However, KANs significantly increase the number of learnable parameters, raising concerns about their effectiveness in data-scarce environments. This paper presents a comprehensive comparative study of MLPs and KANs from both algorithmic and experimental perspectives, with a focus on low-data regimes. We introduce an effective technique for designing MLPs with unique, parameterized activation functions for each neuron, enabling a more balanced comparison with KANs. Using empirical evaluations on simulated data and two real-world data sets from medicine and engineering, we explore the trade-offs between model complexity and accuracy, with particular attention to the role of network depth. Our findings show that MLPs with individualized activation functions achieve significantly higher predictive accuracy with only a modest increase in parameters, especially when the sample size is limited to around one hundred. For example, in a three-class classification problem within additive manufacturing, MLPs achieve a median accuracy of 0.91, significantly outperforming KANs, which only reach a median accuracy of 0.53 with default hyperparameters. These results offer valuable insights into the impact of activation function selection in neural networks.

Kolmogorov-Arnold Transformer

Authors: Xingyi Yang, Xinchao Wang

Citation Count: 19

Abstract: Transformers stand as the cornerstone of mordern deep learning. Traditionally, these models rely on multi-layer perceptron (MLP) layers to mix the information between channels. In this paper, we introduce the Kolmogorov-Arnold Transformer (KAT), a novel architecture that replaces MLP layers with Kolmogorov-Arnold Network (KAN) layers to enhance the expressiveness and performance of the model. Integrating KANs into transformers, however, is no easy feat, especially when scaled up. Specifically, we identify three key challenges: (C1) Base function. The standard B-spline function used in KANs is not optimized for parallel computing on modern hardware, resulting in slower inference speeds. (C2) Parameter and Computation Inefficiency. KAN requires a unique function for each input-output pair, making the computation extremely large. (C3) Weight initialization. The initialization of weights in KANs is particularly challenging due to their learnable activation functions, which are critical for achieving convergence in deep neural networks. To overcome the aforementioned challenges, we propose three key solutions: (S1) Rational basis. We replace B-spline functions with rational functions to improve compatibility with modern GPUs. By implementing this in CUDA, we achieve faster computations. (S2) Group KAN. We share the activation weights through a group of neurons, to reduce the computational load without sacrificing performance. (S3) Variance-preserving initialization. We carefully initialize the activation weights to make sure that the activation variance is maintained across layers. With these designs, KAT scales effectively and readily outperforms traditional MLP-based transformers.

MonoKAN: Certified Monotonic Kolmogorov-Arnold Network

Authors: Alejandro Polo-Molina, David Alfaya, Jose Portela

Citation Count: 2

Abstract: Artificial Neural Networks (ANNs) have significantly advanced various fields by effectively recognizing patterns and solving complex problems. Despite these advancements, their interpretability remains a critical challenge, especially in applications where transparency and accountability are essential. To address this, explainable AI (XAI) has made progress in demystifying ANNs, yet interpretability alone is often insufficient. In certain applications, model predictions must align with expert-imposed requirements, sometimes exemplified by partial monotonicity constraints. While monotonic approaches are found in the literature for traditional Multi-layer Perceptrons (MLPs), they still face difficulties in achieving both interpretability and certified partial monotonicity. Recently, the Kolmogorov-Arnold Network (KAN) architecture, based on learnable activation functions parametrized as splines, has been proposed as a more interpretable alternative to MLPs. Building on this, we introduce a novel ANN architecture called MonoKAN, which is based on the KAN architecture and achieves certified partial monotonicity while enhancing interpretability. To achieve this, we employ cubic Hermite splines, which guarantee monotonicity through a set of straightforward conditions. Additionally, by using positive weights in the linear combinations of these splines, we ensure that the network preserves the monotonic relationships between input and output. Our experiments demonstrate that MonoKAN not only enhances interpretability but also improves predictive performance across the majority of benchmarks, outperforming state-of-the-art monotonic MLP approaches.

Hardware Acceleration of Kolmogorov-Arnold Network (KAN) for Lightweight Edge Inference

Authors: Wei-Hsing Huang, Jianwei Jia, Yuyao Kong, Faaiq Waqar, Tai-Hao Wen, Meng-Fan Chang, Shimeng Yu

Venue: Asia and South Pacific Design Automation Conference

Citation Count: 2

Abstract: Recently, a novel model named Kolmogorov-Arnold Networks (KAN) has been proposed with the potential to achieve the functionality of traditional deep neural networks (DNNs) using orders of magnitude fewer parameters by parameterized B-spline functions with trainable coefficients. However, the B-spline functions in KAN present new challenges for hardware acceleration. Evaluating the B-spline functions can be performed by using look-up tables (LUTs) to directly map the B-spline functions, thereby reducing computational resource requirements. However, this method still requires substantial circuit resources (LUTs, MUXs, decoders, etc.). For the first time, this paper employs an algorithm-hardware co-design methodology to accelerate KAN. The proposed algorithm-level techniques include Alignment-Symmetry and PowerGap KAN hardware aware quantization, KAN sparsity aware mapping strategy, and circuit-level techniques include N:1 Time Modulation Dynamic Voltage input generator with analog-CIM (ACIM) circuits. The impact of non-ideal effects, such as partial sum errors caused by the process variations, has been evaluated with the statistics measured from the TSMC 22nm RRAM-ACIM prototype chips. With the best searched hyperparameters of KAN and the optimized circuits implemented in 22 nm node, we can reduce hardware area by 41.78x, energy by 77.97x with 3.03% accuracy boost compared to the traditional DNN hardware.

ASPINN: An asymptotic strategy for solving singularly perturbed differential equations

Authors: Sen Wang, Peizhi Zhao, Tao Song

Abstract: Solving Singularly Perturbed Differential Equations (SPDEs) presents challenges due to the rapid change of their solutions at the boundary layer. In this manuscript, We propose Asymptotic Physics-Informed Neural Networks (ASPINN), a generalization of Physics-Informed Neural Networks (PINN) and General-Kindred Physics-Informed Neural Networks (GKPINN) approaches. This is a decomposition method based on the idea of asymptotic analysis. Compared to PINN, the ASPINN method has a strong fitting ability for solving SPDEs due to the placement of exponential layers at the boundary layer. Unlike GKPINN, ASPINN lessens the number of fully connected layers, thereby reducing the training cost more effectively. Moreover, ASPINN theoretically approximates the solution at the boundary layer more accurately, which accuracy is also improved compared to GKPINN. We demonstrate the effect of ASPINN by solving diverse classes of SPDEs, which clearly shows that the ASPINN method is promising in boundary layer problems. Furthermore, we introduce Chebyshev Kolmogorov-Arnold Networks (Chebyshev-KAN) instead of MLP, achieving better performance in various experiments.

A preliminary study on continual learning in computer vision using Kolmogorov-Arnold Networks

Authors: Alessandro Cacciatore, Valerio Morelli, Federica Paganica, Emanuele Frontoni, Lucia Migliorelli, Daniele Berardini

Citation Count: 4

Abstract: Deep learning has long been dominated by multi-layer perceptrons (MLPs), which have demonstrated superiority over other optimizable models in various domains. Recently, a new alternative to MLPs has emerged - Kolmogorov-Arnold Networks (KAN)- which are based on a fundamentally different mathematical framework. According to their authors, KANs address several major issues in MLPs, such as catastrophic forgetting in continual learning scenarios. However, this claim has only been supported by results from a regression task on a toy 1D dataset. In this paper, we extend the investigation by evaluating the performance of KANs in continual learning tasks within computer vision, specifically using the MNIST datasets. To this end, we conduct a structured analysis of the behavior of MLPs and two KAN-based models in a class-incremental learning scenario, ensuring that the architectures involved have the same number of trainable parameters. Our results demonstrate that an efficient version of KAN outperforms both traditional MLPs and the original KAN implementation. We further analyze the influence of hyperparameters in MLPs and KANs, as well as the impact of certain trainable parameters in KANs, such as bias and scale weights. Additionally, we provide a preliminary investigation of recent KAN-based convolutional networks and compare their performance with that of traditional convolutional neural networks. Our codes can be found at https://github.com/MrPio/KAN-Continual_Learning_tests.

Higher-order-ReLU-KANs (HRKANs) for solving physics-informed neural networks (PINNs) more accurately, robustly and faster

Authors: Chi Chiu So, Siu Pang Yung

Citation Count: 7

Abstract: Finding solutions to partial differential equations (PDEs) is an important and essential component in many scientific and engineering discoveries. One of the common approaches empowered by deep learning is Physics-informed Neural Networks (PINNs). Recently, a new type of fundamental neural network model, Kolmogorov-Arnold Networks (KANs), has been proposed as a substitute of Multilayer Perceptions (MLPs), and possesses trainable activation functions. To enhance KANs in fitting accuracy, a modification of KANs, so called ReLU-KANs, using “square of ReLU” as the basis of its activation functions, has been suggested. In this work, we propose another basis of activation functions, namely, Higherorder-ReLU (HR), which is simpler than the basis of activation functions used in KANs, namely, Bsplines; allows efficient KAN matrix operations; and possesses smooth and non-zero higher-order derivatives, essential to physicsinformed neural networks. We name such KANs with Higher-order-ReLU (HR) as their activations, HRKANs. Our detailed experiments on two famous and representative PDEs, namely, the linear Poisson equation and nonlinear Burgers’ equation with viscosity, reveal that our proposed Higher-order-ReLU-KANs (HRKANs) achieve the highest fitting accuracy and training robustness and lowest training time significantly among KANs, ReLU-KANs and HRKANs. The codes to replicate our experiments are available at https://github.com/kelvinhkcs/HRKAN.

A Gated Residual Kolmogorov-Arnold Networks for Mixtures of Experts

Authors: Hugo Inzirillo, Remi Genet

Citation Count: 4

Abstract: This paper introduces KAMoE, a novel Mixture of Experts (MoE) framework based on Gated Residual Kolmogorov-Arnold Networks (GRKAN). We propose GRKAN as an alternative to the traditional gating function, aiming to enhance efficiency and interpretability in MoE modeling. Through extensive experiments on digital asset markets and real estate valuation, we demonstrate that KAMoE consistently outperforms traditional MoE architectures across various tasks and model types. Our results show that GRKAN exhibits superior performance compared to standard Gating Residual Networks, particularly in LSTM-based models for sequential tasks. We also provide insights into the trade-offs between model complexity and performance gains in MoE and KAMoE architectures.

Data-driven model discovery with Kolmogorov-Arnold networks

Authors: Mohammadamin Moradi, Shirin Panahi, Erik M. Bollt, Ying-Cheng Lai

Venue: Physical Review Research

Citation Count: 3

Abstract: Data-driven model discovery of complex dynamical systems is typically done using sparse optimization, but it has a fundamental limitation: sparsity in that the underlying governing equations of the system contain only a small number of elementary mathematical terms. Examples where sparse optimization fails abound, such as the classic Ikeda or optical-cavity map in nonlinear dynamics and a large variety of ecosystems. Exploiting the recently articulated Kolmogorov-Arnold networks, we develop a general model-discovery framework for any dynamical systems including those that do not satisfy the sparsity condition. In particular, we demonstrate non-uniqueness in that a large number of approximate models of the system can be found which generate the same invariant set with the correct statistics such as the Lyapunov exponents and Kullback-Leibler divergence. An analogy to shadowing of numerical trajectories in chaotic systems is pointed out.

PPLNs: Parametric Piecewise Linear Networks for Event-Based Temporal Modeling and Beyond

Authors: Chen Song, Zhenxiao Liang, Bo Sun, Qixing Huang

Venue: Neural Information Processing Systems

Abstract: We present Parametric Piecewise Linear Networks (PPLNs) for temporal vision inference. Motivated by the neuromorphic principles that regulate biological neural behaviors, PPLNs are ideal for processing data captured by event cameras, which are built to simulate neural activities in the human retina. We discuss how to represent the membrane potential of an artificial neuron by a parametric piecewise linear function with learnable coefficients. This design echoes the idea of building deep models from learnable parametric functions recently popularized by Kolmogorov-Arnold Networks (KANs). Experiments demonstrate the state-of-the-art performance of PPLNs in event-based and image-based vision applications, including steering prediction, human pose estimation, and motion deblurring. The source code of our implementation is available at https://github.com/chensong1995/PPLN.

October

KANOP: A Data-Efficient Option Pricing Model using Kolmogorov-Arnold Networks

Authors: Rushikesh Handal, Kazuki Matoya, Yunzhuo Wang, Masanori Hirano

Venue: IEEE Conference on Computational Intelligence for Financial Engineering & Economics

Abstract: Inspired by the recently proposed Kolmogorov-Arnold Networks (KANs), we introduce the KAN-based Option Pricing (KANOP) model to value American-style options, building on the conventional Least Square Monte Carlo (LSMC) algorithm. KANs, which are based on Kolmogorov-Arnold representation theorem, offer a data-efficient alternative to traditional Multi-Layer Perceptrons, requiring fewer hidden layers to achieve a higher level of performance. By leveraging the flexibility of KANs, KANOP provides a learnable alternative to the conventional set of basis functions used in the LSMC model, allowing the model to adapt to the pricing task and effectively estimate the expected continuation value. Using examples of standard American and Asian-American options, we demonstrate that KANOP produces more reliable option value estimates, both for single-dimensional cases and in more complex scenarios involving multiple input variables. The delta estimated by the KANOP model is also more accurate than that obtained using conventional basis functions, which is crucial for effective option hedging. Graphical illustrations further validate KANOP’s ability to accurately model the expected continuation value for American-style options.

Incorporating Arbitrary Matrix Group Equivariance into KANs

Authors: Lexiang Hu, Yisen Wang, Zhouchen Lin

Citation Count: 1

Abstract: Kolmogorov-Arnold Networks (KANs) have seen great success in scientific domains thanks to spline activation functions, becoming an alternative to Multi-Layer Perceptrons (MLPs). However, spline functions may not respect symmetry in tasks, which is crucial prior knowledge in machine learning. In this paper, we propose Equivariant Kolmogorov-Arnold Networks (EKAN), a method for incorporating arbitrary matrix group equivariance into KANs, aiming to broaden their applicability to more fields. We first construct gated spline basis functions, which form the EKAN layer together with equivariant linear weights, and then define a lift layer to align the input space of EKAN with the feature space of the dataset, thereby building the entire EKAN architecture. Compared with baseline models, EKAN achieves higher accuracy with smaller datasets or fewer parameters on symmetry-related tasks, such as particle scattering and the three-body problem, often reducing test MSE by several orders of magnitude. Even in non-symbolic formula scenarios, such as top quark tagging with three jet constituents, EKAN achieves comparable results with state-of-the-art equivariant architectures using fewer than 40% of the parameters, while KANs do not outperform MLPs as expected. Code and data are available at https://github.com/hulx2002/EKAN .

Uncertainty Quantification with Bayesian Higher Order ReLU KANs

Authors: James Giroux, Cristiano Fanelli

Venue: Machine Learning: Science and Technology

Citation Count: 1

Abstract: We introduce the first method of uncertainty quantification in the domain of Kolmogorov-Arnold Networks, specifically focusing on (Higher Order) ReLUKANs to enhance computational efficiency given the computational demands of Bayesian methods. The method we propose is general in nature, providing access to both epistemic and aleatoric uncertainties. It is also capable of generalization to other various basis functions. We validate our method through a series of closure tests, including simple one-dimensional functions and application to the domain of (Stochastic) Partial Differential Equations. Referring to the latter, we demonstrate the method’s ability to correctly identify functional dependencies introduced through the inclusion of a stochastic term. The code supporting this work can be found at https://github.com/wmdataphys/Bayesian-HR-KAN

On the expressiveness and spectral bias of KANs

Authors: Yixuan Wang, Jonathan W. Siegel, Ziming Liu, Thomas Y. Hou

Venue: International Conference on Learning Representations

Citation Count: 12

Abstract: Kolmogorov-Arnold Networks (KAN) \cite{liu2024kan} were very recently proposed as a potential alternative to the prevalent architectural backbone of many deep learning models, the multi-layer perceptron (MLP). KANs have seen success in various tasks of AI for science, with their empirical efficiency and accuracy demostrated in function regression, PDE solving, and many more scientific problems. In this article, we revisit the comparison of KANs and MLPs, with emphasis on a theoretical perspective. On the one hand, we compare the representation and approximation capabilities of KANs and MLPs. We establish that MLPs can be represented using KANs of a comparable size. This shows that the approximation and representation capabilities of KANs are at least as good as MLPs. Conversely, we show that KANs can be represented using MLPs, but that in this representation the number of parameters increases by a factor of the KAN grid size. This suggests that KANs with a large grid size may be more efficient than MLPs at approximating certain functions. On the other hand, from the perspective of learning and optimization, we study the spectral bias of KANs compared with MLPs. We demonstrate that KANs are less biased toward low frequencies than MLPs. We highlight that the multi-level learning feature specific to KANs, i.e. grid extension of splines, improves the learning process for high-frequency components. Detailed comparisons with different choices of depth, width, and grid sizes of KANs are made, shedding some light on how to choose the hyperparameters in practice.

Deep Learning Alternatives of the Kolmogorov Superposition Theorem

Authors: Leonardo Ferreira Guilhoto, Paris Perdikaris

Venue: International Conference on Learning Representations

Citation Count: 7

Abstract: This paper explores alternative formulations of the Kolmogorov Superposition Theorem (KST) as a foundation for neural network design. The original KST formulation, while mathematically elegant, presents practical challenges due to its limited insight into the structure of inner and outer functions and the large number of unknown variables it introduces. Kolmogorov-Arnold Networks (KANs) leverage KST for function approximation, but they have faced scrutiny due to mixed results compared to traditional multilayer perceptrons (MLPs) and practical limitations imposed by the original KST formulation. To address these issues, we introduce ActNet, a scalable deep learning model that builds on the KST and overcomes many of the drawbacks of Kolmogorov’s original formulation. We evaluate ActNet in the context of Physics-Informed Neural Networks (PINNs), a framework well-suited for leveraging KST’s strengths in low-dimensional function approximation, particularly for simulating partial differential equations (PDEs). In this challenging setting, where models must learn latent functions without direct measurements, ActNet consistently outperforms KANs across multiple benchmarks and is competitive against the current best MLP-based approaches. These results present ActNet as a promising new direction for KST-based deep learning applications, particularly in scientific computing and PDE simulation tasks.

Model Comparisons: XNet Outperforms KAN

Authors: Xin Li, Zhihong Jeff Xia, Xiaotao Zheng

Abstract: In the fields of computational mathematics and artificial intelligence, the need for precise data modeling is crucial, especially for predictive machine learning tasks. This paper explores further XNet, a novel algorithm that employs the complex-valued Cauchy integral formula, offering a superior network architecture that surpasses traditional Multi-Layer Perceptrons (MLPs) and Kolmogorov-Arnold Networks (KANs). XNet significant improves speed and accuracy across various tasks in both low and high-dimensional spaces, redefining the scope of data-driven model development and providing substantial improvements over established time series models like LSTMs.

Kolmogorov-Arnold Network Autoencoders

Authors: Mohammadamin Moradi, Shirin Panahi, Erik Bollt, Ying-Cheng Lai

Citation Count: 5

Abstract: Deep learning models have revolutionized various domains, with Multi-Layer Perceptrons (MLPs) being a cornerstone for tasks like data regression and image classification. However, a recent study has introduced Kolmogorov-Arnold Networks (KANs) as promising alternatives to MLPs, leveraging activation functions placed on edges rather than nodes. This structural shift aligns KANs closely with the Kolmogorov-Arnold representation theorem, potentially enhancing both model accuracy and interpretability. In this study, we explore the efficacy of KANs in the context of data representation via autoencoders, comparing their performance with traditional Convolutional Neural Networks (CNNs) on the MNIST, SVHN, and CIFAR-10 datasets. Our results demonstrate that KAN-based autoencoders achieve competitive performance in terms of reconstruction accuracy, thereby suggesting their viability as effective tools in data analysis tasks.

MLP-KAN: Unifying Deep Representation and Function Learning

Authors: Yunhong He, Yifeng Xie, Zhengqing Yuan, Lichao Sun

Citation Count: 2

Abstract: Recent advancements in both representation learning and function learning have demonstrated substantial promise across diverse domains of artificial intelligence. However, the effective integration of these paradigms poses a significant challenge, particularly in cases where users must manually decide whether to apply a representation learning or function learning model based on dataset characteristics. To address this issue, we introduce MLP-KAN, a unified method designed to eliminate the need for manual model selection. By integrating Multi-Layer Perceptrons (MLPs) for representation learning and Kolmogorov-Arnold Networks (KANs) for function learning within a Mixture-of-Experts (MoE) architecture, MLP-KAN dynamically adapts to the specific characteristics of the task at hand, ensuring optimal performance. Embedded within a transformer-based framework, our work achieves remarkable results on four widely-used datasets across diverse domains. Extensive experimental evaluation demonstrates its superior versatility, delivering competitive performance across both deep representation and function learning tasks. These findings highlight the potential of MLP-KAN to simplify the model selection process, offering a comprehensive, adaptable solution across various domains. Our code and weights are available at \url{https://github.com/DLYuanGod/MLP-KAN}.

P1-KAN: an effective Kolmogorov-Arnold network with application to hydraulic valley optimization

Author: Xavier Warin

Abstract: A new Kolmogorov-Arnold network (KAN) is proposed to approximate potentially irregular functions in high dimensions. We provide error bounds for this approximation, assuming that the Kolmogorov-Arnold expansion functions are sufficiently smooth. When the function is only continuous, we also provide universal approximation theorems. We show that it outperforms multilayer perceptrons in terms of accuracy and convergence speed. We also compare it with several proposed KAN networks: it outperforms all networks for irregular functions and achieves similar accuracy to the original spline-based KAN network for smooth functions. Finally, we compare some of the KAN networks in optimizing a French hydraulic valley.

Sinc Kolmogorov-Arnold Network and Its Applications on Physics-informed Neural Networks

Authors: Tianchi Yu, Jingwei Qiu, Jiang Yang, Ivan Oseledets

Citation Count: 2

Abstract: In this paper, we propose to use Sinc interpolation in the context of Kolmogorov-Arnold Networks, neural networks with learnable activation functions, which recently gained attention as alternatives to multilayer perceptron. Many different function representations have already been tried, but we show that Sinc interpolation proposes a viable alternative, since it is known in numerical analysis to represent well both smooth functions and functions with singularities. This is important not only for function approximation but also for the solutions of partial differential equations with physics-informed neural networks. Through a series of experiments, we show that SincKANs provide better results in almost all of the examples we have considered.

Quantum Kolmogorov-Arnold networks by combining quantum signal processing circuits

Author: Ammar Daskin

Abstract: In this paper, we show that an equivalent implementation of KAN can be done on quantum computers by simply combining quantum signal processing circuits in layers. This provides a powerful and robust path for the applications of KAN on quantum computers.

QKAN: quantum Kolmogorov-Arnold networks with applications in machine learning and multivariate state preparation

Authors: Petr Ivashkov, Po-Wei Huang, Kelvin Koor, Lirandë Pira, Patrick Rebentrost

Citation Count: 1

Abstract: We introduce quantum Kolmogorov-Arnold networks (QKAN), a quantum algorithmic framework inspired by the recently proposed Kolmogorov-Arnold Networks (KAN). QKAN inherits the compositional structure of KAN and is based on block-encodings, constructed recursively from a single layer using quantum singular value transformation. We demonstrate the algorithmic utility of QKAN in two applications. First, we introduce and analyze QKAN as a quantum learning model, treating the eigenvalues of block-encoded matrices as neurons and applying parametrized activation functions on the edges of the network. We show that QKAN is a wide-and-shallow neural architecture, where shallow depth is compensated by exponentially wide layers whenever efficient block-encodings of inputs are available. We further discuss how to parametrize and train QKAN using parametrized quantum circuits and quantum linear algebra subroutines. Second, we demonstrate that QKAN can serve as a multivariate quantum state-preparation protocol for functions with shallow compositional structure. We demonstrate this by efficiently preparing a multivariate Gaussian quantum state using a two-layer QKAN. Looking forward, we anticipate that QKAN’s compositional and modular design will enable new applications in quantum machine learning and quantum state preparation.

Art Forgery Detection using Kolmogorov Arnold and Convolutional Neural Networks

Authors: Sandro Boccuzzo, Deborah Desirée Meyer, Ludovica Schaerf

Venue: ECCV Workshops

Citation Count: 1

Abstract: Art authentication has historically established itself as a task requiring profound connoisseurship of one particular artist. Nevertheless, famous art forgers such as Wolfgang Beltracchi were able to deceive dozens of art experts. In recent years Artificial Intelligence algorithms have been successfully applied to various image processing tasks. In this work, we leverage the growing improvements in AI to present an art authentication framework for the identification of the forger Wolfgang Beltracchi. Differently from existing literature on AI-aided art authentication, we focus on a specialized model of a forger, rather than an artist, flipping the approach of traditional AI methods. We use a carefully compiled dataset of known artists forged by Beltracchi and a set of known works by the forger to train a multiclass image classification model based on EfficientNet. We compare the results with Kolmogorov Arnold Networks (KAN) which, to the best of our knowledge, have never been tested in the art domain. The results show a general agreement between the different models’ predictions on artworks flagged as forgeries, which are then closely studied using visual analysis.

Residual Kolmogorov-Arnold Network for Enhanced Deep Learning

Authors: Ray Congrui Yu, Sherry Wu, Jiang Gui

Citation Count: 1

Abstract: Despite their immense success, deep convolutional neural networks (CNNs) can be difficult to optimize and costly to train due to hundreds of layers within the network depth. Conventional convolutional operations are fundamentally limited by their linear nature along with fixed activations, where many layers are needed to learn meaningful patterns in data. Because of the sheer size of these networks, this approach is simply computationally inefficient, and poses overfitting or gradient explosion risks, especially in small datasets. As a result, we introduce a “plug-in” module, called Residual Kolmogorov-Arnold Network (RKAN). Our module is highly compact, so it can be easily added into any stage (level) of traditional deep networks, where it learns to integrate supportive polynomial feature transformations to existing convolutional frameworks. RKAN offers consistent improvements over baseline models in different vision tasks and widely tested benchmarks, accomplishing cutting-edge performance on them.

KACQ-DCNN: Uncertainty-Aware Interpretable Kolmogorov-Arnold Classical-Quantum Dual-Channel Neural Network for Heart Disease Detection

Authors: Md Abrar Jahin, Md. Akmol Masud, M. F. Mridha, Zeyar Aung, Nilanjan Dey

Citation Count: 6

Abstract: Heart failure is a leading cause of global mortality, necessitating improved diagnostic strategies. Classical machine learning models struggle with challenges such as high-dimensional data, class imbalances, poor feature representations, and a lack of interpretability. While quantum machine learning holds promise, current hybrid models have not fully exploited quantum advantages. In this paper, we propose the Kolmogorov-Arnold Classical-Quantum Dual-Channel Neural Network (KACQ-DCNN), a novel hybrid architecture that replaces traditional multilayer perceptrons with Kolmogorov-Arnold Networks (KANs), enabling learnable univariate activation functions. Our KACQ-DCNN 4-qubit, 1-layer model outperforms 37 benchmark models, including 16 classical and 12 quantum neural networks, achieving an accuracy of 92.03%, with macro-average precision, recall, and F1 scores of 92.00%. It also achieved a ROC-AUC of 94.77%, surpassing other models by significant margins, as validated by paired t-tests with a significance threshold of 0.0056 (after Bonferroni correction). Ablation studies highlight the synergistic effect of classical-quantum integration, improving performance by about 2% over MLP variants. Additionally, LIME and SHAP explainability techniques enhance feature interpretability, while conformal prediction provides robust uncertainty quantification. Our results demonstrate that KACQ-DCNN improves cardiovascular diagnostics by combining high accuracy with interpretability and uncertainty quantification.

Generalization Bounds and Model Complexity for Kolmogorov-Arnold Networks

Authors: Xianyang Zhang, Huijuan Zhou

Venue: International Conference on Learning Representations

Citation Count: 2

Abstract: Kolmogorov-Arnold Network (KAN) is a network structure recently proposed by Liu et al. (2024) that offers improved interpretability and a more parsimonious design in many science-oriented tasks compared to multi-layer perceptrons. This work provides a rigorous theoretical analysis of KAN by establishing generalization bounds for KAN equipped with activation functions that are either represented by linear combinations of basis functions or lying in a low-rank Reproducing Kernel Hilbert Space (RKHS). In the first case, the generalization bound accommodates various choices of basis functions in forming the activation functions in each layer of KAN and is adapted to different operator norms at each layer. For a particular choice of operator norms, the bound scales with the $l_1$ norm of the coefficient matrices and the Lipschitz constants for the activation functions, and it has no dependence on combinatorial parameters (e.g., number of nodes) outside of logarithmic factors. Moreover, our result does not require the boundedness assumption on the loss function and, hence, is applicable to a general class of regression-type loss functions. In the low-rank case, the generalization bound scales polynomially with the underlying ranks as well as the Lipschitz constants of the activation functions in each layer. These bounds are empirically investigated for KANs trained with stochastic gradient descent on simulated and real data sets. The numerical results demonstrate the practical relevance of these bounds.

On the Convergence of (Stochastic) Gradient Descent for Kolmogorov–Arnold Networks

Authors: Yihang Gao, Vincent Y. F. Tan

Citation Count: 2

Abstract: Kolmogorov–Arnold Networks (KANs), a recently proposed neural network architecture, have gained significant attention in the deep learning community, due to their potential as a viable alternative to multi-layer perceptrons (MLPs) and their broad applicability to various scientific tasks. Empirical investigations demonstrate that KANs optimized via stochastic gradient descent (SGD) are capable of achieving near-zero training loss in various machine learning (e.g., regression, classification, and time series forecasting, etc.) and scientific tasks (e.g., solving partial differential equations). In this paper, we provide a theoretical explanation for the empirical success by conducting a rigorous convergence analysis of gradient descent (GD) and SGD for two-layer KANs in solving both regression and physics-informed tasks. For regression problems, we establish using the neural tangent kernel perspective that GD achieves global linear convergence of the objective function when the hidden dimension of KANs is sufficiently large. We further extend these results to SGD, demonstrating a similar global convergence in expectation. Additionally, we analyze the global convergence of GD and SGD for physics-informed KANs, which unveils additional challenges due to the more complex loss structure. This is the first work establishing the global convergence guarantees for GD and SGD applied to optimize KANs and physics-informed KANs.

The Proof of Kolmogorov-Arnold May Illuminate Neural Network Learning

Author: Michael H. Freedman

Citation Count: 1

Abstract: Kolmogorov and Arnold, in answering Hilbert’s 13th problem (in the context of continuous functions), laid the foundations for the modern theory of Neural Networks (NNs). Their proof divides the representation of a multivariate function into two steps: The first (non-linear) inter-layer map gives a universal embedding of the data manifold into a single hidden layer whose image is patterned in such a way that a subsequent dynamic can then be defined to solve for the second inter-layer map. I interpret this pattern as “minor concentration” of the almost everywhere defined Jacobians of the interlayer map. Minor concentration amounts to sparsity for higher exterior powers of the Jacobians. We present a conceptual argument for how such sparsity may set the stage for the emergence of successively higher order concepts in today’s deep NNs and suggest two classes of experiments to test this hypothesis.

Kolmogorov-Arnold Neural Networks for High-Entropy Alloys Design

Authors: Yagnik Bandyopadhyay, Harshil Avlani, Houlong L. Zhuang

Venue: Modelling and Simulation in Materials Science and Engineering

Citation Count: 2

Abstract: A wide range of deep learning-based machine learning techniques are extensively applied to the design of high-entropy alloys (HEAs), yielding numerous valuable insights. Kolmogorov-Arnold Networks (KAN) is a recently developed architecture that aims to improve both the accuracy and interpretability of input features. In this work, we explore three different datasets for HEA design and demonstrate the application of KAN for both classification and regression models. In the first example, we use a KAN classification model to predict the probability of single-phase formation in high-entropy carbide ceramics based on various properties such as mixing enthalpy and valence electron concentration. In the second example, we employ a KAN regression model to predict the yield strength and ultimate tensile strength of HEAs based on their chemical composition and process conditions including annealing time, cold rolling percentage, and homogenization temperature. The third example involves a KAN classification model to determine whether a certain composition is an HEA or non-HEA, followed by a KAN regressor model to predict the bulk modulus of the identified HEA, aiming to identify HEAs with high bulk modulus. In all three examples, KAN either outperform or match the performance in terms of accuracy such as F1 score for classification and Mean Square Error (MSE), and coefficient of determination (R2) for regression of the multilayer perceptron (MLP) by demonstrating the efficacy of KAN in handling both classification and regression tasks. We provide a promising direction for future research to explore advanced machine learning techniques, which lead to more accurate predictions and better interpretability of complex materials, ultimately accelerating the discovery and optimization of HEAs with desirable properties.

Evaluating Federated Kolmogorov-Arnold Networks on Non-IID Data

Authors: Arthur Mendonça Sasse, Claudio Miceli de Farias

Citation Count: 4

Abstract: Federated Kolmogorov-Arnold Networks (F-KANs) have already been proposed, but their assessment is at an initial stage. We present a comparison between KANs (using B-splines and Radial Basis Functions as activation functions) and Multi- Layer Perceptrons (MLPs) with a similar number of parameters for 100 rounds of federated learning in the MNIST classification task using non-IID partitions with 100 clients. After 15 trials for each model, we show that the best accuracies achieved by MLPs can be achieved by Spline-KANs in half of the time (in rounds), with just a moderate increase in computing time.

WormKAN: Are KAN Effective for Identifying and Tracking Concept Drift in Time Series?

Authors: Kunpeng Xu, Lifei Chen, Shengrui Wang

Abstract: Dynamic concepts in time series are crucial for understanding complex systems such as financial markets, healthcare, and online activity logs. These concepts help reveal structures and behaviors in sequential data for better decision-making and forecasting. However, existing models often struggle to detect and track concept drift due to limitations in interpretability and adaptability. To address this challenge, inspired by the flexibility of the recent Kolmogorov-Arnold Network (KAN), we propose WormKAN, a concept-aware KAN-based model to address concept drift in co-evolving time series. WormKAN consists of three key components: Patch Normalization, Temporal Representation Module, and Concept Dynamics. Patch normalization processes co-evolving time series into patches, treating them as fundamental modeling units to capture local dependencies while ensuring consistent scaling. The temporal representation module learns robust latent representations by leveraging a KAN-based autoencoder, complemented by a smoothness constraint, to uncover inter-patch correlations. Concept dynamics identifies and tracks dynamic transitions, revealing structural shifts in the time series through concept identification and drift detection. These transitions, akin to passing through a \textit{wormhole}, are identified by abrupt changes in the latent space. Experiments show that KAN and KAN-based models (WormKAN) effectively segment time series into meaningful concepts, enhancing the identification and tracking of concept drift.

PointNet with KAN versus PointNet with MLP for 3D Classification and Segmentation of Point Sets

Author: Ali Kashefi

Citation Count: 7

Abstract: Kolmogorov-Arnold Networks (KANs) have recently gained attention as an alternative to traditional Multilayer Perceptrons (MLPs) in deep learning frameworks. KANs have been integrated into various deep learning architectures such as convolutional neural networks, graph neural networks, and transformers, with their performance evaluated. However, their effectiveness within point-cloud-based neural networks remains unexplored. To address this gap, we incorporate KANs into PointNet for the first time to evaluate their performance on 3D point cloud classification and segmentation tasks. Specifically, we introduce PointNet-KAN, built upon two key components. First, it employs KANs instead of traditional MLPs. Second, it retains the core principle of PointNet by using shared KAN layers and applying symmetric functions for global feature extraction, ensuring permutation invariance with respect to the input features. In traditional MLPs, the goal is to train the weights and biases with fixed activation functions; however, in KANs, the goal is to train the activation functions themselves. We use Jacobi polynomials to construct the KAN layers. We extensively and systematically evaluate PointNet-KAN across various polynomial degrees and special types such as the Lagrange, Chebyshev, and Gegenbauer polynomials. Our results show that PointNet-KAN achieves competitive performance compared to PointNet with MLPs on benchmark datasets for 3D object classification and part and semantic segmentation, despite employing a shallower and simpler network architecture. We also study a hybrid PointNet model incorporating both KAN and MLP layers. We hope this work serves as a foundation and provides guidance for integrating KANs, as an alternative to MLPs, into more advanced point cloud processing architectures.

EPi-cKANs: Elasto-Plasticity Informed Kolmogorov-Arnold Networks Using Chebyshev Polynomials

Authors: Farinaz Mostajeran, Salah A Faroughi

Citation Count: 6

Abstract: Multilayer perceptron (MLP) networks are predominantly used to develop data-driven constitutive models for granular materials. They offer a compelling alternative to traditional physics-based constitutive models in predicting nonlinear responses of these materials, e.g., elasto-plasticity, under various loading conditions. To attain the necessary accuracy, MLPs often need to be sufficiently deep or wide, owing to the curse of dimensionality inherent in these problems. To overcome this limitation, we present an elasto-plasticity informed Chebyshev-based Kolmogorov-Arnold network (EPi-cKAN) in this study. This architecture leverages the benefits of KANs and augmented Chebyshev polynomials, as well as integrates physical principles within both the network structure and the loss function. The primary objective of EPi-cKAN is to provide an accurate and generalizable function approximation for non-linear stress-strain relationships, using fewer parameters compared to standard MLPs. To evaluate the efficiency, accuracy, and generalization capabilities of EPi-cKAN in modeling complex elasto-plastic behavior, we initially compare its performance with other cKAN-based models, which include purely data-driven parallel and serial architectures. Furthermore, to differentiate EPi-cKAN’s distinct performance, we also compare it against purely data-driven and physics-informed MLP-based methods. Lastly, we test EPi-cKAN’s ability to predict blind strain-controlled paths that extend beyond the training data distribution to gauge its generalization and predictive capabilities. Our findings indicate that, even with limited data and fewer parameters compared to other approaches, EPi-cKAN provides superior accuracy in predicting stress components and demonstrates better generalization when used to predict sand elasto-plastic behavior under blind triaxial axisymmetric strain-controlled loading paths.

KA-GNN: Kolmogorov-Arnold Graph Neural Networks for Molecular Property Prediction

Authors: Longlong Li, Yipeng Zhang, Guanghui Wang, Kelin Xia

Citation Count: 3

Abstract: As key models in geometric deep learning, graph neural networks have demonstrated enormous power in molecular data analysis. Recently, a specially-designed learning scheme, known as Kolmogorov-Arnold Network (KAN), shows unique potential for the improvement of model accuracy, efficiency, and explainability. Here we propose the first non-trivial Kolmogorov-Arnold Network-based Graph Neural Networks (KA-GNNs), including KAN-based graph convolutional networks(KA-GCN) and KAN-based graph attention network (KA-GAT). The essential idea is to utilizes KAN’s unique power to optimize GNN architectures at three major levels, including node embedding, message passing, and readout. Further, with the strong approximation capability of Fourier series, we develop Fourier series-based KAN model and provide a rigorous mathematical prove of the robust approximation capability of this Fourier KAN architecture. To validate our KA-GNNs, we consider seven most-widely-used benchmark datasets for molecular property prediction and extensively compare with existing state-of-the-art models. It has been found that our KA-GNNs can outperform traditional GNN models. More importantly, our Fourier KAN module can not only increase the model accuracy but also reduce the computational time. This work not only highlights the great power of KA-GNNs in molecular property prediction but also provides a novel geometric deep learning framework for the general non-Euclidean data analysis.

Baseflow identification via explainable AI with Kolmogorov-Arnold networks

Authors: Chuyang Liu, Tirthankar Roy, Daniel M. Tartakovsky, Dipankar Dwivedi

Abstract: Hydrological models often involve constitutive laws that may not be optimal in every application. We propose to replace such laws with the Kolmogorov-Arnold networks (KANs), a class of neural networks designed to identify symbolic expressions. We demonstrate KAN’s potential on the problem of baseflow identification, a notoriously challenging task plagued by significant uncertainty. KAN-derived functional dependencies of the baseflow components on the aridity index outperform their original counterparts. On a test set, they increase the Nash-Sutcliffe Efficiency (NSE) by 67%, decrease the root mean squared error by 30%, and increase the Kling-Gupta efficiency by 24%. This superior performance is achieved while reducing the number of fitting parameters from three to two. Next, we use data from 378 catchments across the continental United States to refine the water-balance equation at the mean-annual scale. The KAN-derived equations based on the refined water balance outperform both the current aridity index model, with up to a 105% increase in NSE, and the KAN-derived equations based on the original water balance. While the performance of our model and tree-based machine learning methods is similar, KANs offer the advantage of simplicity and transparency and require no specific software or computational tools. This case study focuses on the aridity index formulation, but the approach is flexible and transferable to other hydrological processes.

From PINNs to PIKANs: Recent Advances in Physics-Informed Machine Learning

Authors: Juan Diego Toscano, Vivek Oommen, Alan John Varghese, Zongren Zou, Nazanin Ahmadi Daryakenari, Chenxi Wu, George Em Karniadakis

Citation Count: 25

Abstract: Physics-Informed Neural Networks (PINNs) have emerged as a key tool in Scientific Machine Learning since their introduction in 2017, enabling the efficient solution of ordinary and partial differential equations using sparse measurements. Over the past few years, significant advancements have been made in the training and optimization of PINNs, covering aspects such as network architectures, adaptive refinement, domain decomposition, and the use of adaptive weights and activation functions. A notable recent development is the Physics-Informed Kolmogorov-Arnold Networks (PIKANS), which leverage a representation model originally proposed by Kolmogorov in 1957, offering a promising alternative to traditional PINNs. In this review, we provide a comprehensive overview of the latest advancements in PINNs, focusing on improvements in network design, feature expansion, optimization techniques, uncertainty quantification, and theoretical insights. We also survey key applications across a range of fields, including biomedicine, fluid and solid mechanics, geophysics, dynamical systems, heat transfer, chemical engineering, and beyond. Finally, we review computational frameworks and software tools developed by both academia and industry to support PINN research and applications.

Multifidelity Kolmogorov-Arnold Networks

Authors: Amanda A. Howard, Bruno Jacob, Panos Stinis

Citation Count: 4

Abstract: We develop a method for multifidelity Kolmogorov-Arnold networks (KANs), which use a low-fidelity model along with a small amount of high-fidelity data to train a model for the high-fidelity data accurately. Multifidelity KANs (MFKANs) reduce the amount of expensive high-fidelity data needed to accurately train a KAN by exploiting the correlations between the low- and high-fidelity data to give accurate and robust predictions in the absence of a large high-fidelity dataset. In addition, we show that multifidelity KANs can be used to increase the accuracy of physics-informed KANs (PIKANs), without the use of training data.

HiPPO-KAN: Efficient KAN Model for Time Series Analysis

Authors: SangJong Lee, Jin-Kwang Kim, JunHo Kim, TaeHan Kim, James Lee

Citation Count: 2

Abstract: In this study, we introduces a parameter-efficient model that outperforms traditional models in time series forecasting, by integrating High-order Polynomial Projection (HiPPO) theory into the Kolmogorov-Arnold network (KAN) framework. This HiPPO-KAN model achieves superior performance on long sequence data without increasing parameter count. Experimental results demonstrate that HiPPO-KAN maintains a constant parameter count while varying window sizes and prediction horizons, in contrast to KAN, whose parameter count increases linearly with window size. Surprisingly, although the HiPPO-KAN model keeps a constant parameter count as increasing window size, it significantly outperforms KAN model at larger window sizes. These results indicate that HiPPO-KAN offers significant parameter efficiency and scalability advantages for time series forecasting. Additionally, we address the lagging problem commonly encountered in time series forecasting models, where predictions fail to promptly capture sudden changes in the data. We achieve this by modifying the loss function to compute the MSE directly on the coefficient vectors in the HiPPO domain. This adjustment effectively resolves the lagging problem, resulting in predictions that closely follow the actual time series data. By incorporating HiPPO theory into KAN, this study showcases an efficient approach for handling long sequences with improved predictive accuracy, offering practical contributions for applications in large-scale time series data.

Architectural Scaling Surpass Basis Complexity? Efficient KANs with Single-Parameter Design

Authors: Zhijie Chen, Xinglin Zhang, Hongshu Guo, Yue-Jiao Gong

Citation Count: 5

Abstract: The landscape of Kolmogorov-Arnold Networks (KANs) is rapidly expanding, yet lacks a unified theoretical framework and a clear principle for efficient architecture design. This paper addresses these gaps with three core contributions. First, we introduce the Universal KAN (Uni-KAN) framework, a novel abstraction that formally unifies all KAN-style networks through dense and sparse representations. We prove their interchangeability and provide an open-source library for this framework, facilitating future research. Second, we propose the Efficient KAN Expansion (EKE) Hypothesis, a design philosophy positing that allocating parameters to architectural scaling rather than basis function complexity yields superior performance. Third, we present Single-Parameter KANs (SKANs), a family of ultra-lightweight networks that embody the EKE Hypothesis. Our comprehensive experiments provide the first strong empirical validation for the theoretical necessity of basis function smoothness for stable training. Furthermore, SKANs demonstrate state-of-the-art performance, improving F1 scores by up to 6.51\% and reducing test loss by 93.1\%, while achieving up to 6x faster training speeds compared to existing KAN variants. These results establish a robust framework, a guiding hypothesis, and a practical methodology for designing the next generation of efficient and powerful neural networks. The code is accessible at https://anonymous.4open.science/r/SKAN-EBBB/.

Kaninfradet3D:A Road-side Camera-LiDAR Fusion 3D Perception Model based on Nonlinear Feature Extraction and Intrinsic Correlation

Authors: Pei Liu, Nanfang Zheng, Yiqun Li, Junlan Chen, Ziyuan Pu

Citation Count: 1

Abstract: With the development of AI-assisted driving, numerous methods have emerged for ego-vehicle 3D perception tasks, but there has been limited research on roadside perception. With its ability to provide a global view and a broader sensing range, the roadside perspective is worth developing. LiDAR provides precise three-dimensional spatial information, while cameras offer semantic information. These two modalities are complementary in 3D detection. However, adding camera data does not increase accuracy in some studies since the information extraction and fusion procedure is not sufficiently reliable. Recently, Kolmogorov-Arnold Networks (KANs) have been proposed as replacements for MLPs, which are better suited for high-dimensional, complex data. Both the camera and the LiDAR provide high-dimensional information, and employing KANs should enhance the extraction of valuable features to produce better fusion outcomes. This paper proposes Kaninfradet3D, which optimizes the feature extraction and fusion modules. To extract features from complex high-dimensional data, the model’s encoder and fuser modules were improved using KAN Layers. Cross-attention was applied to enhance feature fusion, and visual comparisons verified that camera features were more evenly integrated. This addressed the issue of camera features being abnormally concentrated, negatively impacting fusion. Compared to the benchmark, our approach shows improvements of +9.87 mAP and +10.64 mAP in the two viewpoints of the TUMTraf Intersection Dataset and an improvement of +1.40 mAP in the roadside end of the TUMTraf V2X Cooperative Perception Dataset. The results indicate that Kaninfradet3D can effectively fuse features, demonstrating the potential of applying KANs in roadside perception tasks.

KANICE: Kolmogorov-Arnold Networks with Interactive Convolutional Elements

Authors: Md Meftahul Ferdaus, Mahdi Abdelguerfi, Elias Ioup, David Dobson, Kendall N. Niles, Ken Pathak, Steven Sloan

Venue: International Conference on AI-ML-Systems

Citation Count: 5

Abstract: We introduce KANICE (Kolmogorov-Arnold Networks with Interactive Convolutional Elements), a novel neural architecture that combines Convolutional Neural Networks (CNNs) with Kolmogorov-Arnold Network (KAN) principles. KANICE integrates Interactive Convolutional Blocks (ICBs) and KAN linear layers into a CNN framework. This leverages KANs’ universal approximation capabilities and ICBs’ adaptive feature learning. KANICE captures complex, non-linear data relationships while enabling dynamic, context-dependent feature extraction based on the Kolmogorov-Arnold representation theorem. We evaluated KANICE on four datasets: MNIST, Fashion-MNIST, EMNIST, and SVHN, comparing it against standard CNNs, CNN-KAN hybrids, and ICB variants. KANICE consistently outperformed baseline models, achieving 99.35% accuracy on MNIST and 90.05% on the SVHN dataset. Furthermore, we introduce KANICE-mini, a compact variant designed for efficiency. A comprehensive ablation study demonstrates that KANICE-mini achieves comparable performance to KANICE with significantly fewer parameters. KANICE-mini reached 90.00% accuracy on SVHN with 2,337,828 parameters, compared to KANICE’s 25,432,000. This study highlights the potential of KAN-based architectures in balancing performance and computational efficiency in image classification tasks. Our work contributes to research in adaptive neural networks, integrates mathematical theorems into deep learning architectures, and explores the trade-offs between model complexity and performance, advancing computer vision and pattern recognition. The source code for this paper is publicly accessible through our GitHub repository (https://github.com/m-ferdaus/kanice).

NIDS Neural Networks Using Sliding Time Window Data Processing with Trainable Activations and its Generalization Capability

Authors: Anton Raskovalov, Nikita Gabdullin, Ilya Androsov

Abstract: This paper presents neural networks for network intrusion detection systems (NIDS), that operate on flow data preprocessed with a time window. It requires only eleven features which do not rely on deep packet inspection and can be found in most NIDS datasets and easily obtained from conventional flow collectors. The time window aggregates information with respect to hosts facilitating the identification of flow signatures that are missed by other aggregation methods. Several network architectures are studied and the use of Kolmogorov-Arnold Network (KAN)-inspired trainable activation functions that help to achieve higher accuracy with simpler network structure is proposed. The reported training accuracy exceeds 99% for the proposed method with as little as twenty neural network input features. This work also studies the generalization capability of NIDS, a crucial aspect that has not been adequately addressed in the previous studies. The generalization experiments are conducted using CICIDS2017 dataset and a custom dataset collected as part of this study. It is shown that the performance metrics decline significantly when changing datasets, and the reduction in performance metrics can be attributed to the difference in signatures of the same type flows in different datasets, which in turn can be attributed to the differences between the underlying networks. It is shown that the generalization accuracy of some neural networks can be very unstable and sensitive to random initialization parameters, and neural networks with fewer parameters and well-tuned activations are more stable and achieve higher accuracy.

LArctan-SKAN: Simple and Efficient Single-Parameterized Kolmogorov-Arnold Networks using Learnable Trigonometric Function

Authors: Zhijie Chen, Xinglin Zhang

Citation Count: 2

Abstract: This paper proposes a novel approach for designing Single-Parameterized Kolmogorov-Arnold Networks (SKAN) by utilizing a Single-Parameterized Function (SFunc) constructed from trigonometric functions. Three new SKAN variants are developed: LSin-SKAN, LCos-SKAN, and LArctan-SKAN. Experimental validation on the MNIST dataset demonstrates that LArctan-SKAN excels in both accuracy and computational efficiency. Specifically, LArctan-SKAN significantly improves test set accuracy over existing models, outperforming all pure KAN variants compared, including FourierKAN, LSS-SKAN, and Spl-KAN. It also surpasses mixed MLP-based models such as MLP+rKAN and MLP+fKAN in accuracy. Furthermore, LArctan-SKAN exhibits remarkable computational efficiency, with a training speed increase of 535.01% and 49.55% compared to MLP+rKAN and MLP+fKAN, respectively. These results confirm the effectiveness and potential of SKANs constructed with trigonometric functions. The experiment code is available at https://github.com/chikkkit/LArctan-SKAN .

KANsformer for Scalable Beamforming

Authors: Xinke Xie, Yang Lu, Chong-Yung Chi, Wei Chen, Bo Ai, Dusit Niyato

Venue: IEEE Transactions on Vehicular Technology

Citation Count: 1

Abstract: This paper proposes an unsupervised deep-learning (DL) approach by integrating transformer and Kolmogorov-Arnold networks (KAN) termed KANsformer to realize scalable beamforming for mobile communication systems. Specifically, we consider a classic multi-input-single-output energy efficiency maximization problem subject to the total power budget. The proposed KANsformer first extracts hidden features via a multi-head self-attention mechanism and then reads out the desired beamforming design via KAN. Numerical results are provided to evaluate the KANsformer in terms of generalization performance, transfer learning and ablation experiment. Overall, the KANsformer outperforms existing benchmark DL approaches, and is adaptable to the change in the number of mobile users with real-time and near-optimal inference.

Using Structural Similarity and Kolmogorov-Arnold Networks for Anatomical Embedding of Cortical Folding Patterns

Authors: Minheng Chen, Chao Cao, Tong Chen, Yan Zhuang, Jing Zhang, Yanjun Lyu, Xiaowei Yu, Lu Zhang, Tianming Liu, Dajiang Zhu

Venue: IEEE International Symposium on Biomedical Imaging

Citation Count: 1

Abstract: The 3-hinge gyrus (3HG) is a newly defined folding pattern, which is the conjunction of gyri coming from three directions in cortical folding. Many studies demonstrated that 3HGs can be reliable nodes when constructing brain networks or connectome since they simultaneously possess commonality and individuality across different individual brains and populations. However, 3HGs are identified and validated within individual spaces, making it difficult to directly serve as the brain network nodes due to the absence of cross-subject correspondence. The 3HG correspondences represent the intrinsic regulation of brain organizational architecture, traditional image-based registration methods tend to fail because individual anatomical properties need to be fully respected. To address this challenge, we propose a novel self-supervised framework for anatomical feature embedding of the 3HGs to build the correspondences among different brains. The core component of this framework is to construct a structural similarity-enhanced multi-hop feature encoding strategy based on the recently developed Kolmogorov-Arnold network (KAN) for anatomical feature embedding. Extensive experiments suggest that our approach can effectively establish robust cross-subject correspondences when no one-to-one mapping exists.

November

KAN-AD: Time Series Anomaly Detection with Kolmogorov-Arnold Networks

Authors: Quan Zhou, Changhua Pei, Fei Sun, Jing Han, Zhengwei Gao, Dan Pei, Haiming Zhang, Gaogang Xie, Jianhui Li

Citation Count: 4

Abstract: Time series anomaly detection (TSAD) underpins real-time monitoring in cloud services and web systems, allowing rapid identification of anomalies to prevent costly failures. Most TSAD methods driven by forecasting models tend to overfit by emphasizing minor fluctuations. Our analysis reveals that effective TSAD should focus on modeling “normal” behavior through smooth local patterns. To achieve this, we reformulate time series modeling as approximating the series with smooth univariate functions. The local smoothness of each univariate function ensures that the fitted time series remains resilient against local disturbances. However, a direct KAN implementation proves susceptible to these disturbances due to the inherently localized characteristics of B-spline functions. We thus propose KAN-AD, replacing B-splines with truncated Fourier expansions and introducing a novel lightweight learning mechanism that emphasizes global patterns while staying robust to local disturbances. On four popular TSAD benchmarks, KAN-AD achieves an average 15% improvement in detection accuracy (with peaks exceeding 27%) over state-of-the-art baselines. Remarkably, it requires fewer than 1,000 trainable parameters, resulting in a 50% faster inference speed compared to the original KAN, demonstrating the approach’s efficiency and practical viability.

A KAN-based Interpretable Framework for Process-Informed Prediction of Global Warming Potential

Authors: Jaewook Lee, Xinyang Sun, Ethan Errington, Miao Guo

Abstract: Accurate prediction of Global Warming Potential (GWP) is essential for assessing the environmental impact of chemical processes and materials. Traditional GWP prediction models rely predominantly on molecular structure, overlooking critical process-related information. In this study, we present an integrative GWP prediction model that combines molecular descriptors (MACCS keys and Mordred descriptors) with process information (process title, description, and location) to improve predictive accuracy and interpretability. Using a deep neural network (DNN) model, we achieved an R-squared of 86% on test data with Mordred descriptors, process location, and description information, representing a 25% improvement over the previous benchmark of 61%; XAI analysis further highlighted the significant role of process title embeddings in enhancing model predictions. To enhance interpretability, we employed a Kolmogorov-Arnold Network (KAN) to derive a symbolic formula for GWP prediction, capturing key molecular and process features and providing a transparent, interpretable alternative to black-box models, enabling users to gain insights into the molecular and process factors influencing GWP. Error analysis showed that the model performs reliably in densely populated data ranges, with increased uncertainty for higher GWP values. This analysis allows users to manage prediction uncertainty effectively, supporting data-driven decision-making in chemical and process design. Our results suggest that integrating both molecular and process-level information in GWP prediction models yields substantial gains in accuracy and interpretability, offering a valuable tool for sustainability assessments. Future work may extend this approach to additional environmental impact categories and refine the model to further enhance its predictive reliability.

Integrating Symbolic Neural Networks with Building Physics: A Study and Proposal

Authors: Xia Chen, Guoquan Lv, Xinwei Zhuang, Carlos Duarte, Stefano Schiavon, Philipp Geyer

Citation Count: 1

Abstract: Symbolic neural networks, such as Kolmogorov-Arnold Networks (KAN), offer a promising approach for integrating prior knowledge with data-driven methods, making them valuable for addressing inverse problems in scientific and engineering domains. This study explores the application of KAN in building physics, focusing on predictive modeling, knowledge discovery, and continuous learning. Through four case studies, we demonstrate KAN’s ability to rediscover fundamental equations, approximate complex formulas, and capture time-dependent dynamics in heat transfer. While there are challenges in extrapolation and interpretability, we highlight KAN’s potential to combine advanced modeling methods for knowledge augmentation, which benefits energy efficiency, system optimization, and sustainability assessments beyond the personal knowledge constraints of the modelers. Additionally, we propose a model selection decision tree to guide practitioners in appropriate applications for building physics.

Fairness-Utilization Trade-off in Wireless Networks with Explainable Kolmogorov-Arnold Networks

Authors: Masoud Shokrnezhad, Hamidreza Mazandarani, Tarik Taleb

Venue: 2024 IEEE Virtual Conference on Communications (VCC)

Citation Count: 1

Abstract: The effective distribution of user transmit powers is essential for the significant advancements that the emergence of 6G wireless networks brings. In recent studies, Deep Neural Networks (DNNs) have been employed to address this challenge. However, these methods frequently encounter issues regarding fairness and computational inefficiency when making decisions, rendering them unsuitable for future dynamic services that depend heavily on the participation of each individual user. To address this gap, this paper focuses on the challenge of transmit power allocation in wireless networks, aiming to optimize $α$-fairness to balance network utilization and user equity. We introduce a novel approach utilizing Kolmogorov-Arnold Networks (KANs), a class of machine learning models that offer low inference costs compared to traditional DNNs through superior explainability. The study provides a comprehensive problem formulation, establishing the NP-hardness of the power allocation problem. Then, two algorithms are proposed for dataset generation and decentralized KAN training, offering a flexible framework for achieving various fairness objectives in dynamic 6G environments. Extensive numerical simulations demonstrate the effectiveness of our approach in terms of fairness and inference cost. The results underscore the potential of KANs to overcome the limitations of existing DNN-based methods, particularly in scenarios that demand rapid adaptation and fairness.

Human-in-the-Loop Feature Selection Using Interpretable Kolmogorov-Arnold Network-based Double Deep Q-Network

Authors: Md Abrar Jahin, M. F. Mridha, Nilanjan Dey, Md. Jakir Hossen

Abstract: Feature selection is critical for improving the performance and interpretability of machine learning models, particularly in high-dimensional spaces where complex feature interactions can reduce accuracy and increase computational demands. Existing approaches often rely on static feature subsets or manual intervention, limiting adaptability and scalability. However, dynamic, per-instance feature selection methods and model-specific interpretability in reinforcement learning remain underexplored. This study proposes a human-in-the-loop (HITL) feature selection framework integrated into a Double Deep Q-Network (DDQN) using a Kolmogorov-Arnold Network (KAN). Our novel approach leverages simulated human feedback and stochastic distribution-based sampling, specifically Beta, to iteratively refine feature subsets per data instance, improving flexibility in feature selection. The KAN-DDQN achieved notable test accuracies of 93% on MNIST and 83% on FashionMNIST, outperforming conventional MLP-DDQN models by up to 9%. The KAN-based model provided high interpretability via symbolic representation while using 4 times fewer neurons in the hidden layer than MLPs did. Comparatively, the models without feature selection achieved test accuracies of only 58% on MNIST and 64% on FashionMNIST, highlighting significant gains with our framework. We further validate scalability on CIFAR-10 and CIFAR-100, achieving up to 30% relative macro F1 improvement on MNIST and 5% on CIFAR-10, while reducing calibration error by 25%. Complexity analysis confirms real-time feasibility with latency below 1 ms and parameter counts under 0.02M. Pruning and visualization further enhanced model transparency by elucidating decision pathways. These findings present a scalable, interpretable solution for feature selection that is suitable for applications requiring real-time, adaptive decision-making with minimal human oversight.

Physics-informed Kolmogorov-Arnold Network with Chebyshev Polynomials for Fluid Mechanics

Authors: Chunyu Guo, Lucheng Sun, Shilong Li, Zelong Yuan, Chao Wang

Citation Count: 4

Abstract: Solving partial differential equations (PDEs) is essential in scientific forecasting and fluid dynamics. Traditional approaches often incur expensive computational costs and trade-offs in efficiency and accuracy. Recent deep neural networks have improved the accuracy but require high-quality training data. Physics-informed neural networks (PINNs) effectively integrate physical laws to reduce the data reliance in limited sample scenarios. A novel machine-learning framework, Chebyshev physics-informed Kolmogorov–Arnold network (ChebPIKAN), is proposed to integrate the robust architectures of Kolmogorov–Arnold networks (KAN) with physical constraints to enhance the calculation accuracy of PDEs for fluid mechanics. We study the fundamentals of KAN, take advantage of the orthogonality of Chebyshev polynomial basis functions in spline fitting, and integrate physics-informed loss functions that are tailored to specific PDEs in fluid dynamics, including Allen–Cahn equation, nonlinear Burgers equation, Helmholtz equations, Kovasznay flow, cylinder wake flow, and cavity flow. Extensive experiments demonstrate that the proposed ChebPIKAN model significantly outperforms the standard KAN architecture in solving various PDEs by effectively embedding essential physical information. These results indicate that augmenting KAN with physical constraints can alleviate the overfitting issues of KAN and improve the extrapolation performance. Consequently, this study highlights the potential of ChebPIKAN as a powerful tool in computational fluid dynamics and propose a path toward fast and reliable predictions in fluid mechanics and beyond.

On Training of Kolmogorov-Arnold Networks

Author: Shairoz Sohail

Citation Count: 1

Abstract: Kolmogorov-Arnold Networks have recently been introduced as a flexible alternative to multi-layer Perceptron architectures. In this paper, we examine the training dynamics of different KAN architectures and compare them with corresponding MLP formulations. We train with a variety of different initialization schemes, optimizers, and learning rates, as well as utilize back propagation free approaches like the HSIC Bottleneck. We find that (when judged by test accuracy) KANs are an effective alternative to MLP architectures on high-dimensional datasets and have somewhat better parameter efficiency, but suffer from more unstable training dynamics. Finally, we provide recommendations for improving training stability of larger KAN models.

A Survey on Kolmogorov-Arnold Network

Authors: Shriyank Somvanshi, Syed Aaqib Javed, Md Monzurul Islam, Diwas Pandit, Subasish Das

Venue: ACM Computing Surveys

Citation Count: 23

Abstract: This systematic review explores the theoretical foundations, evolution, applications, and future potential of Kolmogorov-Arnold Networks (KAN), a neural network model inspired by the Kolmogorov-Arnold representation theorem. KANs distinguish themselves from traditional neural networks by using learnable, spline-parameterized functions instead of fixed activation functions, allowing for flexible and interpretable representations of high-dimensional functions. This review details KAN’s architectural strengths, including adaptive edge-based activation functions that improve parameter efficiency and scalability in applications such as time series forecasting, computational biomedicine, and graph learning. Key advancements, including Temporal-KAN, FastKAN, and Partial Differential Equation (PDE) KAN, illustrate KAN’s growing applicability in dynamic environments, enhancing interpretability, computational efficiency, and adaptability for complex function approximation tasks. Additionally, this paper discusses KAN’s integration with other architectures, such as convolutional, recurrent, and transformer-based models, showcasing its versatility in complementing established neural networks for tasks requiring hybrid approaches. Despite its strengths, KAN faces computational challenges in high-dimensional and noisy data settings, motivating ongoing research into optimization strategies, regularization techniques, and hybrid models. This paper highlights KAN’s role in modern neural architectures and outlines future directions to improve its computational efficiency, interpretability, and scalability in data-intensive applications.

Early Prediction of Natural Gas Pipeline Leaks Using the MKTCN Model

Authors: Xuguang Li, Zhonglin Zuo, Zheng Dong, Yang Yang

Citation Count: 2

Abstract: Natural gas pipeline leaks pose severe risks, leading to substantial economic losses and potential hazards to human safety. In this study, we develop an accurate model for the early prediction of pipeline leaks. To the best of our knowledge, unlike previous anomaly detection, this is the first application to use internal pipeline data for early prediction of leaks. The modeling process addresses two main challenges: long-term dependencies and sample imbalance. First, we introduce a dilated convolution-based prediction model to capture long-term dependencies, as dilated convolution expands the model’s receptive field without added computational cost. Second, to mitigate sample imbalance, we propose the MKTCN model, which incorporates the Kolmogorov-Arnold Network as the fully connected layer in a dilated convolution model, enhancing network generalization. Finally, we validate the MKTCN model through extensive experiments on two real-world datasets. Results demonstrate that MKTCN outperforms in generalization and classification, particularly under severe data imbalance, and effectively predicts leaks up to 5000 seconds in advance. Overall, the MKTCN model represents a significant advancement in early pipeline leak prediction, providing robust generalization and improved modeling of the long-term dependencies inherent in multi-dimensional time-series data.

SPIKANs: Separable Physics-Informed Kolmogorov-Arnold Networks

Authors: Bruno Jacob, Amanda A. Howard, Panos Stinis

Citation Count: 7

Abstract: Physics-Informed Neural Networks (PINNs) have emerged as a promising method for solving partial differential equations (PDEs) in scientific computing. While PINNs typically use multilayer perceptrons (MLPs) as their underlying architecture, recent advancements have explored alternative neural network structures. One such innovation is the Kolmogorov-Arnold Network (KAN), which has demonstrated benefits over traditional MLPs, including faster neural scaling and better interpretability. The application of KANs to physics-informed learning has led to the development of Physics-Informed KANs (PIKANs), enabling the use of KANs to solve PDEs. However, despite their advantages, KANs often suffer from slower training speeds, particularly in higher-dimensional problems where the number of collocation points grows exponentially with the dimensionality of the system. To address this challenge, we introduce Separable Physics-Informed Kolmogorov-Arnold Networks (SPIKANs). This novel architecture applies the principle of separation of variables to PIKANs, decomposing the problem such that each dimension is handled by an individual KAN. This approach drastically reduces the computational complexity of training without sacrificing accuracy, facilitating their application to higher-dimensional PDEs. Through a series of benchmark problems, we demonstrate the effectiveness of SPIKANs, showcasing their superior scalability and performance compared to PIKANs and highlighting their potential for solving complex, high-dimensional PDEs in scientific computing.

Can KAN Work? Exploring the Potential of Kolmogorov-Arnold Networks in Computer Vision

Authors: Yueyang Cang, Yu hang liu, Li Shi

Abstract: Kolmogorov-Arnold Networks(KANs), as a theoretically efficient neural network architecture, have garnered attention for their potential in capturing complex patterns. However, their application in computer vision remains relatively unexplored. This study first analyzes the potential of KAN in computer vision tasks, evaluating the performance of KAN and its convolutional variants in image classification and semantic segmentation. The focus is placed on examining their characteristics across varying data scales and noise levels. Results indicate that while KAN exhibits stronger fitting capabilities, it is highly sensitive to noise, limiting its robustness. To address this challenge, we propose a smoothness regularization method and introduce a Segment Deactivation technique. Both approaches enhance KAN’s stability and generalization, demonstrating its potential in handling complex visual data tasks.

KLCBL: An Improved Police Incident Classification Model

Authors: Liu Zhuoxian, Shi Tuo, Hu Xiaofeng

Abstract: Police incident data is crucial for public security intelligence, yet grassroots agencies struggle with efficient classification due to manual inefficiency and automated system limitations, especially in telecom and online fraud cases. This research proposes a multichannel neural network model, KLCBL, integrating Kolmogorov-Arnold Networks (KAN), a linguistically enhanced text preprocessing approach (LERT), Convolutional Neural Network (CNN), and Bidirectional Long Short-Term Memory (BiLSTM) for police incident classification. Evaluated with real data, KLCBL achieved 91.9% accuracy, outperforming baseline models. The model addresses classification challenges, enhances police informatization, improves resource allocation, and offers broad applicability to other classification tasks.

EAPCR: A Universal Feature Extractor for Scientific Data without Explicit Feature Relation Patterns

Authors: Zhuohang Yu, Ling An, Yansong Li, Yu Wu, Zeyu Dong, Zhangdi Liu, Le Gao, Zhenyu Zhang, Chichun Zhou

Citation Count: 1

Abstract: Conventional methods, including Decision Tree (DT)-based methods, have been effective in scientific tasks, such as non-image medical diagnostics, system anomaly detection, and inorganic catalysis efficiency prediction. However, most deep-learning techniques have struggled to surpass or even match this level of success as traditional machine-learning methods. The primary reason is that these applications involve multi-source, heterogeneous data where features lack explicit relationships. This contrasts with image data, where pixels exhibit spatial relationships; textual data, where words have sequential dependencies; and graph data, where nodes are connected through established associations. The absence of explicit Feature Relation Patterns (FRPs) presents a significant challenge for deep learning techniques in scientific applications that are not image, text, and graph-based. In this paper, we introduce EAPCR, a universal feature extractor designed for data without explicit FRPs. Tested across various scientific tasks, EAPCR consistently outperforms traditional methods and bridges the gap where deep learning models fall short. To further demonstrate its robustness, we synthesize a dataset without explicit FRPs. While Kolmogorov-Arnold Network (KAN) and feature extractors like Convolutional Neural Networks (CNNs), Graph Convolutional Networks (GCNs), and Transformers struggle, EAPCR excels, demonstrating its robustness and superior performance in scientific tasks without FRPs.

Hybrid deep additive neural networks

Authors: Gyu Min Kim, Jeong Min Jeon

Abstract: Traditional neural networks (multi-layer perceptrons) have become an important tool in data science due to their success across a wide range of tasks. However, their performance is sometimes unsatisfactory, and they often require a large number of parameters, primarily due to their reliance on the linear combination structure. Meanwhile, additive regression has been a popular alternative to linear regression in statistics. In this work, we introduce novel deep neural networks that incorporate the idea of additive regression. Our neural networks share architectural similarities with Kolmogorov-Arnold networks but are based on simpler yet flexible activation and basis functions. Additionally, we introduce several hybrid neural networks that combine this architecture with that of traditional neural networks. We derive their universal approximation properties and demonstrate their effectiveness through simulation studies and a real-data application. The numerical results indicate that our neural networks generally achieve better performance than traditional neural networks while using fewer parameters.

KAT to KANs: A Review of Kolmogorov-Arnold Networks and the Neural Leap Forward

Authors: Divesh Basina, Joseph Raj Vishal, Aarya Choudhary, Bharatesh Chakravarthi

Abstract: The curse of dimensionality poses a significant challenge to modern multilayer perceptron-based architectures, often causing performance stagnation and scalability issues. Addressing this limitation typically requires vast amounts of data. In contrast, Kolmogorov-Arnold Networks have gained attention in the machine learning community for their bold claim of being unaffected by the curse of dimensionality. This paper explores the Kolmogorov-Arnold representation theorem and the mathematical principles underlying Kolmogorov-Arnold Networks, which enable their scalability and high performance in high-dimensional spaces. We begin with an introduction to foundational concepts necessary to understand Kolmogorov-Arnold Networks, including interpolation methods and Basis-splines, which form their mathematical backbone. This is followed by an overview of perceptron architectures and the Universal approximation theorem, a key principle guiding modern machine learning. This is followed by an overview of the Kolmogorov-Arnold representation theorem, including its mathematical formulation and implications for overcoming dimensionality challenges. Next, we review the architecture and error-scaling properties of Kolmogorov-Arnold Networks, demonstrating how these networks achieve true freedom from the curse of dimensionality. Finally, we discuss the practical viability of Kolmogorov-Arnold Networks, highlighting scenarios where their unique capabilities position them to excel in real-world applications. This review aims to offer insights into Kolmogorov-Arnold Networks’ potential to redefine scalability and performance in high-dimensional learning tasks.

KAN/MultKAN with Physics-Informed Spline fitting (KAN-PISF) for ordinary/partial differential equation discovery of nonlinear dynamic systems

Authors: Ashish Pal, Satish Nagarajaiah

Abstract: Machine learning for scientific discovery is increasingly becoming popular because of its ability to extract and recognize the nonlinear characteristics from the data. The black-box nature of deep learning methods poses difficulties in interpreting the identified model. There is a dire need to interpret the machine learning models to develop a physical understanding of dynamic systems. An interpretable form of neural network called Kolmogorov-Arnold networks (KAN) or Multiplicative KAN (MultKAN) offers critical features that help recognize the nonlinearities in the governing ordinary/partial differential equations (ODE/PDE) of various dynamic systems and find their equation structures. In this study, an equation discovery framework is proposed that includes i) sequentially regularized derivatives for denoising (SRDD) algorithm to denoise the measure data to obtain accurate derivatives, ii) KAN to identify the equation structure and suggest relevant nonlinear functions that are used to create a small overcomplete library of functions, and iii) physics-informed spline fitting (PISF) algorithm to filter the excess functions from the library and converge to the correct equation. The framework was tested on the forced Duffing oscillator, Van der Pol oscillator (stiff ODE), Burger’s equation, and Bouc-Wen model (coupled ODE). The proposed method converged to the true equation for the first three systems. It provided an approximate model for the Bouc-Wen model that could acceptably capture the hysteresis response. Using KAN maintains low complexity, which helps the user interpret the results throughout the process and avoid the black-box-type nature of machine learning methods.

KAN-Mamba FusionNet: Redefining Medical Image Segmentation with Non-Linear Modeling

Authors: Akansh Agrawal, Akshan Agrawal, Shashwat Gupta, Priyanka Bagade

Citation Count: 3

Abstract: Medical image segmentation is essential for applications like robotic surgeries, disease diagnosis, and treatment planning. Recently, various deep-learning models have been proposed to enhance medical image segmentation. One promising approach utilizes Kolmogorov-Arnold Networks (KANs), which better capture non-linearity in input data. However, they are unable to effectively capture long-range dependencies, which are required to accurately segment complex medical images and, by that, improve diagnostic accuracy in clinical settings. Neural networks such as Mamba can handle long-range dependencies. However, they have a limited ability to accurately capture non-linearities in the images as compared to KANs. Thus, we propose a novel architecture, the KAN-Mamba FusionNet, which improves segmentation accuracy by effectively capturing the non-linearities from input and handling long-range dependencies with the newly proposed KAMBA block. We evaluated the proposed KAN-Mamba FusionNet on three distinct medical image segmentation datasets: BUSI, Kvasir-Seg, and GlaS - and found it consistently outperforms state-of-the-art methods in IoU and F1 scores. Further, we examined the effects of various components and assessed their contributions to the overall model performance via ablation studies. The findings highlight the effectiveness of this methodology for reliable medical image segmentation, providing a unique approach to address intricate visual data issues in healthcare.

Contrast Similarity-Aware Dual-Pathway Mamba for Multivariate Time Series Node Classification

Authors: Mingsen Du, Meng Chen, Yongjian Li, Xiuxin Zhang, Jiahui Gao, Cun Ji, Shoushui Wei

Citation Count: 1

Abstract: Multivariate time series (MTS) data is generated through multiple sensors across various domains such as engineering application, health monitoring, and the internet of things, characterized by its temporal changes and high dimensional characteristics. Over the past few years, many studies have explored the long-range dependencies and similarities in MTS. However, long-range dependencies are difficult to model due to their temporal changes and high dimensionality makes it difficult to obtain similarities effectively and efficiently. Thus, to address these issues, we propose contrast similarity-aware dual-pathway Mamba for MTS node classification (CS-DPMamba). Firstly, to obtain the dynamic similarity of each sample, we initially use temporal contrast learning module to acquire MTS representations. And then we construct a similarity matrix between MTS representations using Fast Dynamic Time Warping (FastDTW). Secondly, we apply the DPMamba to consider the bidirectional nature of MTS, allowing us to better capture long-range and short-range dependencies within the data. Finally, we utilize the Kolmogorov-Arnold Network enhanced Graph Isomorphism Network to complete the information interaction in the matrix and MTS node classification task. By comprehensively considering the long-range dependencies and dynamic similarity features, we achieved precise MTS node classification. We conducted experiments on multiple University of East Anglia (UEA) MTS datasets, which encompass diverse application scenarios. Our results demonstrate the superiority of our method through both supervised and semi-supervised experiments on the MTS classification task.

Dressing the Imagination: A Dataset for AI-Powered Translation of Text into Fashion Outfits and A Novel NeRA Adapter for Enhanced Feature Adaptation

Authors: Gayatri Deshmukh, Somsubhra De, Chirag Sehgal, Jishu Sen Gupta, Sparsh Mittal

Abstract: Specialized datasets that capture the fashion industry’s rich language and styling elements can boost progress in AI-driven fashion design. We present FLORA, (Fashion Language Outfit Representation for Apparel Generation), the first comprehensive dataset containing 4,330 curated pairs of fashion outfits and corresponding textual descriptions. Each description utilizes industry-specific terminology and jargon commonly used by professional fashion designers, providing precise and detailed insights into the outfits. Hence, the dataset captures the delicate features and subtle stylistic elements necessary to create high-fidelity fashion designs. We demonstrate that fine-tuning generative models on the FLORA dataset significantly enhances their capability to generate accurate and stylistically rich images from textual descriptions of fashion sketches. FLORA will catalyze the creation of advanced AI models capable of comprehending and producing subtle, stylistically rich fashion designs. It will also help fashion designers and end-users to bring their ideas to life. As a second orthogonal contribution, we introduce NeRA (Nonlinear low-rank Expressive Representation Adapter), a novel adapter architecture based on Kolmogorov-Arnold Networks (KAN). Unlike traditional PEFT techniques such as LoRA, LoKR, DoRA, and LoHA that use MLP adapters, NeRA uses learnable spline-based nonlinear transformations, enabling superior modeling of complex semantic relationships, achieving strong fidelity, faster convergence and semantic alignment. Extensive experiments on our proposed FLORA and LAION-5B datasets validate the superiority of NeRA over existing adapters. We will open-source both the FLORA dataset and our implementation code.

Machine Learning Insights into Quark-Antiquark Interactions: Probing Field Distributions and String Tension in QCD

Authors: Wei Kou, Xurong Chen

Venue: The European Physical Journal C

Citation Count: 2

Abstract: Understanding the interactions between quark-antiquark pairs is essential for elucidating quark confinement within the framework of quantum chromodynamics (QCD). This study investigates the field distribution patterns that arise between these pairs by employing advanced machine learning techniques, namely multilayer perceptrons (MLP) and Kolmogorov-Arnold networks (KAN), to analyze data obtained from lattice QCD simulations. The models developed through this training are then applied to calculate the string tension and width associated with chromo flux tubes, and these results are rigorously compared to those derived from lattice QCD. Moreover, we introduce a preliminary analytical expression that characterizes the field distribution as a function of quark separation, utilizing the KAN methodology. Our comprehensive quantitative analysis underscores the potential of integrating machine learning approaches into conventional QCD research.

Exploring Kolmogorov-Arnold Networks for Interpretable Time Series Classification

Authors: Irina Barašin, Blaž Bertalanič, Mihael Mohorčič, Carolina Fortuna

Citation Count: 2

Abstract: Time series classification is a relevant step supporting decision-making processes in various domains, and deep neural models have shown promising performance in this respect. Despite significant advancements in deep learning, the theoretical understanding of how and why complex architectures function remains limited, prompting the need for more interpretable models. Recently, the Kolmogorov-Arnold Networks (KANs) have been proposed as a more interpretable alternative to deep learning. While KAN-related research is significantly rising, to date, the study of KAN architectures for time series classification has been limited. In this paper, we aim to conduct a comprehensive and robust exploration of the KAN architecture for time series classification utilising 117 datasets from UCR benchmark archive, from multiple different domains. More specifically, we investigate a) the transferability of reference architectures designed for regression to classification tasks, b) identifying the hyperparameter and implementation configurations for an architecture that best generalizes across 117 datasets, c) the associated complexity trade-offs and d) evaluate KANs interpretability. Our results demonstrate that (1) the Efficient KAN outperforms MLPs in both performance and training times, showcasing its suitability for classification tasks. (2) Efficient KAN exhibits greater stability than the original KAN across grid sizes, depths, and layer configurations, especially when lower learning rates are employed. (3) KAN achieves competitive accuracy compared to state-of-the-art models such as HIVE-COTE2 and InceptionTime, while maintaining smaller architectures and faster training times, highlighting its favorable balance of performance and transparency. (4) The interpretability of the KAN model, as confirmed by SHAP analysis, reinforces its capacity for transparent decision-making.

Learnable Activation Functions in Physics-Informed Neural Networks for Solving Partial Differential Equations

Authors: Afrah Farea, Mustafa Serdar Celebi

Citation Count: 1

Abstract: Physics-Informed Neural Networks (PINNs) have emerged as a promising approach for solving Partial Differential Equations (PDEs). However, they face challenges related to spectral bias (the tendency to learn low-frequency components while struggling with high-frequency features) and unstable convergence dynamics (mainly stemming from the multi-objective nature of the PINN loss function). These limitations impact their accuracy for problems involving rapid oscillations, sharp gradients, and complex boundary behaviors. We systematically investigate learnable activation functions as a solution to these challenges, comparing Multilayer Perceptrons (MLPs) using fixed and learnable activation functions against Kolmogorov-Arnold Networks (KANs) that employ learnable basis functions. Our evaluation spans diverse PDE types, including linear and non-linear wave problems, mixed-physics systems, and fluid dynamics. Using empirical Neural Tangent Kernel (NTK) analysis and Hessian eigenvalue decomposition, we assess spectral bias and convergence stability of the models. Our results reveal a trade-off between expressivity and training convergence stability. While learnable activation functions work well in simpler architectures, they encounter scalability issues in complex networks due to the higher functional dimensionality. Counterintuitively, we find that low spectral bias alone does not guarantee better accuracy, as functions with broader NTK eigenvalue spectra may exhibit convergence instability. We demonstrate that activation function selection remains inherently problem-specific, with different bases showing distinct advantages for particular PDE characteristics. We believe these insights will help in the design of more robust neural PDE solvers.

GrokFormer: Graph Fourier Kolmogorov-Arnold Transformers

Authors: Guoguo Ai, Guansong Pang, Hezhe Qiao, Yuan Gao, Hui Yan

Abstract: Graph Transformers (GTs) have demonstrated remarkable performance in graph representation learning over popular graph neural networks (GNNs). However, self–attention, the core module of GTs, preserves only low-frequency signals in graph features, leading to ineffectiveness in capturing other important signals like high-frequency ones. Some recent GT models help alleviate this issue, but their flexibility and expressiveness are still limited since the filters they learn are fixed on predefined graph spectrum or spectral order. To tackle this challenge, we propose a Graph Fourier Kolmogorov-Arnold Transformer (GrokFormer), a novel GT model that learns highly expressive spectral filters with adaptive graph spectrum and spectral order through a Fourier series modeling over learnable activation functions. We demonstrate theoretically and empirically that the proposed GrokFormer filter offers better expressiveness than other spectral methods. Comprehensive experiments on 10 real-world node classification datasets across various domains, scales, and graph properties, as well as 5 graph classification datasets, show that GrokFormer outperforms state-of-the-art GTs and GNNs. Our code is available at https://github.com/GGA23/GrokFormer

KACDP: A Highly Interpretable Credit Default Prediction Model

Authors: Kun Liu, Jin Zhao

Abstract: In the field of finance, the prediction of individual credit default is of vital importance. However, existing methods face problems such as insufficient interpretability and transparency as well as limited performance when dealing with high-dimensional and nonlinear data. To address these issues, this paper introduces a method based on Kolmogorov-Arnold Networks (KANs). KANs is a new type of neural network architecture with learnable activation functions and no linear weights, which has potential advantages in handling complex multi-dimensional data. Specifically, this paper applies KANs to the field of individual credit risk prediction for the first time and constructs the Kolmogorov-Arnold Credit Default Predict (KACDP) model. Experiments show that the KACDP model outperforms mainstream credit default prediction models in performance metrics (ROC_AUC and F1 values). Meanwhile, through methods such as feature attribution scores and visualization of the model structure, the model’s decision-making process and the importance of different features are clearly demonstrated, providing transparent and interpretable decision-making basis for financial institutions and meeting the industry’s strict requirements for model interpretability. In conclusion, the KACDP model constructed in this paper exhibits excellent predictive performance and satisfactory interpretability in individual credit risk prediction, providing an effective way to address the limitations of existing methods and offering a new and practical credit risk prediction tool for financial institutions.

KAN See Your Face

Authors: Dong Han, Yong Li, Joachim Denzler

Citation Count: 3

Abstract: With the advancement of face reconstruction (FR) systems, privacy-preserving face recognition (PPFR) has gained popularity for its secure face recognition, enhanced facial privacy protection, and robustness to various attacks. Besides, specific models and algorithms are proposed for face embedding protection by mapping embeddings to a secure space. However, there is a lack of studies on investigating and evaluating the possibility of extracting face images from embeddings of those systems, especially for PPFR. In this work, we introduce the first approach to exploit Kolmogorov-Arnold Network (KAN) for conducting embedding-to-face attacks against state-of-the-art (SOTA) FR and PPFR systems. Face embedding mapping (FEM) models are proposed to learn the distribution mapping relation between the embeddings from the initial domain and target domain. In comparison with Multi-Layer Perceptrons (MLP), we provide two variants, FEM-KAN and FEM-MLP, for efficient non-linear embedding-to-embedding mapping in order to reconstruct realistic face images from the corresponding face embedding. To verify our methods, we conduct extensive experiments with various PPFR and FR models. We also measure reconstructed face images with different metrics to evaluate the image quality. Through comprehensive experiments, we demonstrate the effectiveness of FEMs in accurate embedding mapping and face reconstruction.

KANs for Computer Vision: An Experimental Study

Authors: Karthik Mohan, Hanxiao Wang, Xiatian Zhu

Citation Count: 3

Abstract: This paper presents an experimental study of Kolmogorov-Arnold Networks (KANs) applied to computer vision tasks, particularly image classification. KANs introduce learnable activation functions on edges, offering flexible non-linear transformations compared to traditional pre-fixed activation functions with specific neural work like Multi-Layer Perceptrons (MLPs) and Convolutional Neural Networks (CNNs). While KANs have shown promise mostly in simplified or small-scale datasets, their effectiveness for more complex real-world tasks such as computer vision tasks remains less explored. To fill this gap, this experimental study aims to provide extended observations and insights into the strengths and limitations of KANs. We reveal that although KANs can perform well in specific vision tasks, they face significant challenges, including increased hyperparameter sensitivity and higher computational costs. These limitations suggest that KANs require architectural adaptations, such as integration with other architectures, to be practical for large-scale vision problems. This study focuses on empirical findings rather than proposing new methods, aiming to inform future research on optimizing KANs, in particular computer vision applications or alike.

MvKeTR: Chest CT Report Generation with Multi-View Perception and Knowledge Enhancement

Authors: Xiwei Deng, Xianchun He, Jianfeng Bao, Yudan Zhou, Shuhui Cai, Congbo Cai, Zhong Chen

Citation Count: 1

Abstract: CT report generation (CTRG) aims to automatically generate diagnostic reports for 3D volumes, relieving clinicians’ workload and improving patient care. Despite clinical value, existing works fail to effectively incorporate diagnostic information from multiple anatomical views and lack related clinical expertise essential for accurate and reliable diagnosis. To resolve these limitations, we propose a novel Multi-view perception Knowledge-enhanced TansfoRmer (MvKeTR) to mimic the diagnostic workflow of clinicians. Just as radiologists first examine CT scans from multiple planes, a Multi-View Perception Aggregator (MVPA) with view-aware attention is proposed to synthesize diagnostic information from multiple anatomical views effectively. Then, inspired by how radiologists further refer to relevant clinical records to guide diagnostic decision-making, a Cross-Modal Knowledge Enhancer (CMKE) is devised to retrieve the most similar reports based on the query volume to incorporate domain knowledge into the diagnosis procedure. Furthermore, instead of traditional MLPs, we employ Kolmogorov-Arnold Networks (KANs) as the fundamental building blocks of both modules, which exhibit superior parameter efficiency and reduced spectral bias to better capture high-frequency components critical for CT interpretation while mitigating overfitting. Extensive experiments on the public CTRG-Chest-548 K dataset demonstrate that our method outpaces prior state-of-the-art (SOTA) models across almost all metrics. The code is available at https://github.com/xiweideng/MvKeTR.

Non-linear Equalization in 112 Gb/s PONs Using Kolmogorov-Arnold Networks

Authors: Rodrigo Fischer, Patrick Matalla, Sebastian Randel, Laurent Schmalen

Citation Count: 1

Abstract: We investigate Kolmogorov-Arnold networks (KANs) for non-linear equalization of 112 Gb/s PAM4 passive optical networks (PONs). Using pruning and extensive hyperparameter search, we outperform linear equalizers and convolutional neural networks at low computational complexity.

December

Option Pricing with Convolutional Kolmogorov-Arnold Networks

Authors: Zeyuan Li, Qingdao Huang

Abstract: With the rapid advancement of neural networks, methods for option pricing have evolved significantly. This study employs the Black-Scholes-Merton (B-S-M) model, incorporating an additional variable to improve the accuracy of predictions compared to the traditional Black-Scholes (B-S) model. Furthermore, Convolutional Kolmogorov-Arnold Networks (Conv-KANs) and Kolmogorov-Arnold Networks (KANs) are introduced to demonstrate that networks with enhanced non-linear capabilities yield superior fitting performance. For comparative analysis, Conv-LSTM and LSTM models, which are widely used in time series forecasting, are also applied. Additionally, a novel data selection strategy is proposed to simulate a real trading environment, thereby enhancing the robustness of the model.

Explainable fault and severity classification for rolling element bearings using Kolmogorov-Arnold networks

Authors: Spyros Rigas, Michalis Papachristou, Ioannis Sotiropoulos, Georgios Alexandridis

Abstract: Rolling element bearings are critical components of rotating machinery, with their performance directly influencing the efficiency and reliability of industrial systems. At the same time, bearing faults are a leading cause of machinery failures, often resulting in costly downtime, reduced productivity, and, in extreme cases, catastrophic damage. This study presents a methodology that utilizes Kolmogorov-Arnold Networks to address these challenges through automatic feature selection, hyperparameter tuning and interpretable fault analysis within a unified framework. By training shallow network architectures and minimizing the number of selected features, the framework produces lightweight models that deliver explainable results through feature attribution and symbolic representations of their activation functions. Validated on two widely recognized datasets for bearing fault diagnosis, the framework achieved perfect F1-Scores for fault detection and high performance in fault and severity classification tasks, including 100% F1-Scores in most cases. Notably, it demonstrated adaptability by handling diverse fault types, such as imbalance and misalignment, within the same dataset. The symbolic representations enhanced model interpretability, while feature attribution offered insights into the optimal feature types or signals for each studied task. These results highlight the framework’s potential for practical applications, such as real-time machinery monitoring, and for scientific research requiring efficient and explainable models.

ECG-SleepNet: Deep Learning-Based Comprehensive Sleep Stage Classification Using ECG Signals

Authors: Poorya Aghaomidi, Ge Wang

Citation Count: 1

Abstract: Accurate sleep stage classification is essential for understanding sleep disorders and improving overall health. This study proposes a novel three-stage approach for sleep stage classification using ECG signals, offering a more accessible alternative to traditional methods that often rely on complex modalities like EEG. In Stages 1 and 2, we initialize the weights of two networks, which are then integrated in Stage 3 for comprehensive classification. In the first phase, we estimate key features using Feature Imitating Networks (FINs) to achieve higher accuracy and faster convergence. The second phase focuses on identifying the N1 sleep stage through the time-frequency representation of ECG signals. Finally, the third phase integrates models from the previous stages and employs a Kolmogorov-Arnold Network (KAN) to classify five distinct sleep stages. Additionally, data augmentation techniques, particularly SMOTE, are used in enhancing classification capabilities for underrepresented stages like N1. Our results demonstrate significant improvements in the classification performance, with an overall accuracy of 80.79% an overall kappa of 0.73. The model achieves specific accuracies of 86.70% for Wake, 60.36% for N1, 83.89% for N2, 84.85% for N3, and 87.16% for REM. This study emphasizes the importance of weight initialization and data augmentation in optimizing sleep stage classification with ECG signals.

Beyond Tree Models: A Hybrid Model of KAN and gMLP for Large-Scale Financial Tabular Data

Authors: Mingming Zhang, Jiahao Hu, Pengfei Shi, Ningtao Wang, Ruizhe Gao, Guandong Sun, Feng Zhao, Yulin kang, Xing Fu, Weiqiang Wang, Junbo Zhao

Citation Count: 1

Abstract: Tabular data plays a critical role in real-world financial scenarios. Traditionally, tree models have dominated in handling tabular data. However, financial datasets in the industry often encounter some challenges, such as data heterogeneity, the predominance of numerical features and the large scale of the data, which can range from tens of millions to hundreds of millions of records. These challenges can lead to significant memory and computational issues when using tree-based models. Consequently, there is a growing need for neural network-based solutions that can outperform these models. In this paper, we introduce TKGMLP, an hybrid network for tabular data that combines shallow Kolmogorov Arnold Networks with Gated Multilayer Perceptron. This model leverages the strengths of both architectures to improve performance and scalability. We validate TKGMLP on a real-world credit scoring dataset, where it achieves state-of-the-art results and outperforms current benchmarks. Furthermore, our findings demonstrate that the model continues to improve as the dataset size increases, making it highly scalable. Additionally, we propose a novel feature encoding method for numerical data, specifically designed to address the predominance of numerical features in financial datasets. The integration of this feature encoding method within TKGMLP significantly improves prediction accuracy. This research not only advances table prediction technology but also offers a practical and effective solution for handling large-scale numerical tabular data in various industrial applications.

Enhanced Photovoltaic Power Forecasting: An iTransformer and LSTM-Based Model Integrating Temporal and Covariate Interactions

Authors: Guang Wu, Yun Wang, Qian Zhou, Ziyang Zhang

Venue: 2024 IEEE 8th Conference on Energy Internet and Energy System Integration (EI2)

Citation Count: 2

Abstract: Accurate photovoltaic (PV) power forecasting is critical for integrating renewable energy sources into the grid, optimizing real-time energy management, and ensuring energy reliability amidst increasing demand. However, existing models often struggle with effectively capturing the complex relationships between target variables and covariates, as well as the interactions between temporal dynamics and multivariate data, leading to suboptimal forecasting accuracy. To address these challenges, we propose a novel model architecture that leverages the iTransformer for feature extraction from target variables and employs long short-term memory (LSTM) to extract features from covariates. A cross-attention mechanism is integrated to fuse the outputs of both models, followed by a Kolmogorov-Arnold network (KAN) mapping for enhanced representation. The effectiveness of the proposed model is validated using publicly available datasets from Australia, with experiments conducted across four seasons. Results demonstrate that the proposed model effectively capture seasonal variations in PV power generation and improve forecasting accuracy.

CIKAN: Constraint Informed Kolmogorov-Arnold Networks for Autonomous Spacecraft Rendezvous using Time Shift Governor

Authors: Taehyeun Kim, Anouck Girard, Ilya Kolmanovsky

Citation Count: 3

Abstract: The paper considers a Constrained-Informed Neural Network (CINN) approximation for the Time Shift Governor (TSG), which is an add-on scheme to the nominal closed-loop system used to enforce constraints by time-shifting the reference trajectory in spacecraft rendezvous applications. We incorporate Kolmogorov-Arnold Networks (KANs), an emerging architecture in the AI community, as a fundamental component of CINN and propose a Constrained-Informed Kolmogorov-Arnold Network (CIKAN)-based approximation for TSG. We demonstrate the effectiveness of the CIKAN-based TSG through simulations of constrained spacecraft rendezvous missions on highly elliptic orbits and present comparisons between CIKANs, MLP-based CINNs, and the conventional TSG.

You KAN Do It in a Single Shot: Plug-and-Play Methods with Single-Instance Priors

Authors: Yanqi Cheng, Carola-Bibiane Schönlieb, Angelica I Aviles-Rivero

Abstract: The use of Plug-and-Play (PnP) methods has become a central approach for solving inverse problems, with denoisers serving as regularising priors that guide optimisation towards a clean solution. In this work, we introduce KAN-PnP, an optimisation framework that incorporates Kolmogorov-Arnold Networks (KANs) as denoisers within the Plug-and-Play (PnP) paradigm. KAN-PnP is specifically designed to solve inverse problems with single-instance priors, where only a single noisy observation is available, eliminating the need for large datasets typically required by traditional denoising methods. We show that KANs, based on the Kolmogorov-Arnold representation theorem, serve effectively as priors in such settings, providing a robust approach to denoising. We prove that the KAN denoiser is Lipschitz continuous, ensuring stability and convergence in optimisation algorithms like PnP-ADMM, even in the context of single-shot learning. Additionally, we provide theoretical guarantees for KAN-PnP, demonstrating its convergence under key conditions: the convexity of the data fidelity term, Lipschitz continuity of the denoiser, and boundedness of the regularisation functional. These conditions are crucial for stable and reliable optimisation. Our experimental results show, on super-resolution and joint optimisation, that KAN-PnP outperforms exiting methods, delivering superior performance in single-shot learning with minimal data. The method exhibits strong convergence properties, achieving high accuracy with fewer iterations.

Accurate Surrogate Amplitudes with Calibrated Uncertainties

Authors: Henning Bahl, Nina Elmer, Luigi Favaro, Manuel Haußmann, Tilman Plehn, Ramon Winterhalder

Abstract: Neural networks for LHC physics have to be accurate, reliable, and controlled. Using neural surrogates for the prediction of loop amplitudes as a use case, we first show how activation functions are systematically tested with Kolmogorov-Arnold Networks. Then, we train neural surrogates to simultaneously predict the target amplitude and an uncertainty for the prediction. We disentangle systematic uncertainties, learned by a well-defined likelihood loss, from statistical uncertainties, which require the introduction of Bayesian neural networks or repulsive ensembles. We test the coverage of the learned uncertainties using pull distributions to quantify the calibration of cutting-edge neural surrogates.

PowerMLP: An Efficient Version of KAN

Authors: Ruichen Qiu, Yibo Miao, Shiwen Wang, Lijia Yu, Yifan Zhu, Xiao-Shan Gao

Venue: AAAI Conference on Artificial Intelligence

Citation Count: 2

Abstract: The Kolmogorov-Arnold Network (KAN) is a new network architecture known for its high accuracy in several tasks such as function fitting and PDE solving. The superior expressive capability of KAN arises from the Kolmogorov-Arnold representation theorem and learnable spline functions. However, the computation of spline functions involves multiple iterations, which renders KAN significantly slower than MLP, thereby increasing the cost associated with model training and deployment. The authors of KAN have also noted that ``the biggest bottleneck of KANs lies in its slow training. KANs are usually 10x slower than MLPs, given the same number of parameters.’’ To address this issue, we propose a novel MLP-type neural network PowerMLP that employs simpler non-iterative spline function representation, offering approximately the same training time as MLP while theoretically demonstrating stronger expressive power than KAN. Furthermore, we compare the FLOPs of KAN and PowerMLP, quantifying the faster computation speed of PowerMLP. Our comprehensive experiments demonstrate that PowerMLP generally achieves higher accuracy and a training speed about 40 times faster than KAN in various tasks.

Granger Causality Detection with Kolmogorov-Arnold Networks

Authors: Hongyu Lin, Mohan Ren, Paolo Barucca, Tomaso Aste

Citation Count: 2

Abstract: Discovering causal relationships in time series data is central in many scientific areas, ranging from economics to climate science. Granger causality is a powerful tool for causality detection. However, its original formulation is limited by its linear form and only recently nonlinear machine-learning generalizations have been introduced. This study contributes to the definition of neural Granger causality models by investigating the application of Kolmogorov-Arnold networks (KANs) in Granger causality detection and comparing their capabilities against multilayer perceptrons (MLP). In this work, we develop a framework called Granger Causality KAN (GC-KAN) along with a tailored training approach designed specifically for Granger causality detection. We test this framework on both Vector Autoregressive (VAR) models and chaotic Lorenz-96 systems, analysing the ability of KANs to sparsify input features by identifying Granger causal relationships, providing a concise yet accurate model for Granger causality detection. Our findings show the potential of KANs to outperform MLPs in discerning interpretable Granger causal relationships, particularly for the ability of identifying sparse Granger causality patterns in high-dimensional settings, and more generally, the potential of AI in causality discovery for the dynamical laws in physical systems.

Scattering-Based Structural Inversion of Soft Materials via Kolmogorov-Arnold Networks

Authors: Chi-Huan Tung, Lijie Ding, Ming-Ching Chang, Guan-Rong Huang, Lionel Porcar, Yangyang Wang, Jan-Michael Y. Carrillo, Bobby G. Sumpter, Yuya Shinohara, Changwoo Do, Wei-Ren Chen

Venue: Journal of Chemical Physics

Citation Count: 2

Abstract: Small-angle scattering (SAS) techniques are indispensable tools for probing the structure of soft materials. However, traditional analytical models often face limitations in structural inversion for complex systems, primarily due to the absence of closed-form expressions of scattering functions. To address these challenges, we present a machine learning framework based on the Kolmogorov-Arnold Network (KAN) for directly extracting real-space structural information from scattering spectra in reciprocal space. This model-independent, data-driven approach provides a versatile solution for analyzing intricate configurations in soft matter. By applying the KAN to lyotropic lamellar phases and colloidal suspensions – two representative soft matter systems – we demonstrate its ability to accurately and efficiently resolve structural collectivity and complexity. Our findings highlight the transformative potential of machine learning in enhancing the quantitative analysis of soft materials, paving the way for robust structural inversion across diverse systems.

KKANs: Kurkova-Kolmogorov-Arnold Networks and Their Learning Dynamics

Authors: Juan Diego Toscano, Li-Lian Wang, George Em Karniadakis

Citation Count: 4

Abstract: Inspired by the Kolmogorov-Arnold representation theorem and Kurkova’s principle of using approximate representations, we propose the Kurkova-Kolmogorov-Arnold Network (KKAN), a new two-block architecture that combines robust multi-layer perceptron (MLP) based inner functions with flexible linear combinations of basis functions as outer functions. We first prove that KKAN is a universal approximator, and then we demonstrate its versatility across scientific machine-learning applications, including function regression, physics-informed machine learning (PIML), and operator-learning frameworks. The benchmark results show that KKANs outperform MLPs and the original Kolmogorov-Arnold Networks (KANs) in function approximation and operator learning tasks and achieve performance comparable to fully optimized MLPs for PIML. To better understand the behavior of the new representation models, we analyze their geometric complexity and learning dynamics using information bottleneck theory, identifying three universal learning stages, fitting, transition, and diffusion, across all types of architectures. We find a strong correlation between geometric complexity and signal-to-noise ratio (SNR), with optimal generalization achieved during the diffusion stage. Additionally, we propose self-scaled residual-based attention weights to maintain high SNR dynamically, ensuring uniform convergence and prolonged learning.

From KAN to GR-KAN: Advancing Speech Enhancement with KAN-Based Methodology

Authors: Haoyang Li, Yuchen Hu, Chen Chen, Sabato Marco Siniscalchi, Songting Liu, Eng Siong Chng

Citation Count: 1

Abstract: Deep neural network (DNN)-based speech enhancement (SE) usually uses conventional activation functions, which lack the expressiveness to capture complex multiscale structures needed for high-fidelity SE. Group-Rational KAN (GR-KAN), a variant of Kolmogorov-Arnold Networks (KAN), retains KAN’s expressiveness while improving scalability on complex tasks. We adapt GR-KAN to existing DNN-based SE by replacing dense layers with GR-KAN layers in the time-frequency (T-F) domain MP-SENet and adapting GR-KAN’s activations into the 1D CNN layers in the time-domain Demucs. Results on Voicebank-DEMAND show that GR-KAN requires up to 4x fewer parameters while improving PESQ by up to 0.1. In contrast, KAN, facing scalability issues, outperforms MLP on a small-scale signal modeling task but fails to improve MP-SENet. We demonstrate the first successful use of KAN-based methods for consistent improvement in both time- and SoTA TF-domain SE, establishing GR-KAN as a promising alternative for SE.

Zero Shot Time Series Forecasting Using Kolmogorov Arnold Networks

Authors: Abhiroop Bhattacharya, Nandinee Haq

Abstract: Accurate energy price forecasting is crucial for participants in day-ahead energy markets, as it significantly influences their decision-making processes. While machine learning-based approaches have shown promise in enhancing these forecasts, they often remain confined to the specific markets on which they are trained, thereby limiting their adaptability to new or unseen markets. In this paper, we introduce a cross-domain adaptation model designed to forecast energy prices by learning market-invariant representations across different markets during the training phase. We propose a doubly residual N-BEATS network with Kolmogorov Arnold networks at its core for time series forecasting. These networks, grounded in the Kolmogorov-Arnold representation theorem, offer a powerful way to approximate multivariate continuous functions. The cross domain adaptation model was generated with an adversarial framework. The model’s effectiveness was tested in predicting day-ahead electricity prices in a zero shot fashion. In comparison with baseline models, our proposed framework shows promising results. By leveraging the Kolmogorov-Arnold networks, our model can potentially enhance its ability to capture complex patterns in energy price data, thus improving forecast accuracy across diverse market conditions. This addition not only enriches the model’s representational capacity but also contributes to a more robust and flexible forecasting tool adaptable to various energy markets.

Position reconstruction using deep learning for the HERD PSD beam test

Authors: Longkun Yu, Chenxing Zhang, Dongya Guo, Yaqing Liu, Wenxi Peng, Zhigang Wang, Bing Lu, Rui Qiao, Ke Gong, Jing Wang, Shuai Yang, Yongye Li

Abstract: The High Energy cosmic-Radiation Detection (HERD) facility is a dedicated high energy astronomy and particle physics experiment planned to be installed on the Chinese space station, aiming to detect high-energy cosmic rays (GeV $\sim$ PeV) and high-energy gamma rays ($>$ 500 MeV). The Plastic Scintillator Detector (PSD) is one of the sub-detectors of HERD, with its main function of providing real-time anti-conincidence signals for gamma-ray detection and the secondary function of measuring the charge of cosmic-rays. In 2023, a prototype of PSD was developed and tested at CERN PS&SPS. In this paper, we investigate the position response of the PSD using two reconstruction algorithms: the classic dual-readout ratio and the deep learning method (KAN & MLP neural network). With the latter, we achieved a position resolution of 2 mm (1$σ$), which is significantly better than the classic method.

ProKAN: Progressive Stacking of Kolmogorov-Arnold Networks for Efficient Liver Segmentation

Authors: Bhavesh Gyanchandani, Aditya Oza, Abhinav Roy

Citation Count: 1

Abstract: The growing need for accurate and efficient 3D identification of tumors, particularly in liver segmentation, has spurred considerable research into deep learning models. While many existing architectures offer strong performance, they often face challenges such as overfitting and excessive computational costs. An adjustable and flexible architecture that strikes a balance between time efficiency and model complexity remains an unmet requirement. In this paper, we introduce proKAN, a progressive stacking methodology for Kolmogorov-Arnold Networks (KANs) designed to address these challenges. Unlike traditional architectures, proKAN dynamically adjusts its complexity by progressively adding KAN blocks during training, based on overfitting behavior. This approach allows the network to stop growing when overfitting is detected, preventing unnecessary computational overhead while maintaining high accuracy. Additionally, proKAN utilizes KAN’s learnable activation functions modeled through B-splines, which provide enhanced flexibility in learning complex relationships in 3D medical data. Our proposed architecture achieves state-of-the-art performance in liver segmentation tasks, outperforming standard Multi-Layer Perceptrons (MLPs) and fixed KAN architectures. The dynamic nature of proKAN ensures efficient training times and high accuracy without the risk of overfitting. Furthermore, proKAN provides better interpretability by allowing insight into the decision-making process through its learnable coefficients. The experimental results demonstrate a significant improvement in accuracy, Dice score, and time efficiency, making proKAN a compelling solution for 3D medical image segmentation tasks.

Gamma-Ray Burst Light Curve Reconstruction: A Comparative Machine and Deep Learning Analysis

Authors: A. Manchanda, A. Kaushal, M. G. Dainotti, A. Deepu, S. Naqi, J. Felix, N. Indoriya, S. P. Magesh, H. Gupta, K. Gupta, A. Madhan, D. H. Hartmann, A. Pollo, M. Bogdan, J. X. Prochaska, N. Fraija, D. Debnath

Abstract: Gamma-Ray Bursts (GRBs), observed at high-z, are probes of the evolution of the Universe and can be used as cosmological tools. Thus, we need correlations with small dispersion among key parameters. To reduce such a dispersion, we mitigate gaps in light curves (LCs), including the plateau region, key to building the two-dimensional Dainotti relation between the end time of plateau emission (Ta) and its luminosity (La). We reconstruct LCs using nine models: Multi-Layer Perceptron (MLP), Bi-Mamba, Fourier Transform, Gaussian Process-Random Forest Hybrid (GP-RF), Bidirectional Long Short-Term Memory (Bi-LSTM), Conditional GAN (CGAN), SARIMAX-based Kalman filter, Kolmogorov-Arnold Networks (KANs), and Attention U-Net. These methods are compared to the Willingale model (W07) over a sample of 521 GRBs. MLP and Attention U-Net outperform other methods, with MLP reducing the plateau parameter uncertainties by 37.2% for log Ta, 38.0% for log Fa, and 41.2% for alpha (the post-plateau slope in the W07 model), achieving the lowest 5-fold cross-validation (CV) mean squared error (MSE) of 0.0275. Attention U-Net achieved the lowest uncertainty of parameters, a 37.9% reduction in log Ta, a 38.5% reduction in log Fa and a 41.4% reduction in alpha, but with a higher MSE of 0.134. Although Attention U-Net achieves the largest uncertainty reduction, the MLP attains the lowest test MSE while maintaining comparable uncertainty performance, making it the more reliable model. The other methods yield MSE values ranging from 0.0339 to 0.174. These improvements in parameter precision are needed to use GRBs as standard candles, investigate theoretical models, and predict GRB redshifts through machine learning.

Advancing Parkinson’s Disease Progression Prediction: Comparing Long Short-Term Memory Networks and Kolmogorov-Arnold Networks

Authors: Abhinav Roy, Bhavesh Gyanchandani, Aditya Oza, Abhishek Sharma

Abstract: Parkinson’s Disease (PD) is a degenerative neurological disorder that impairs motor and non-motor functions, significantly reducing quality of life and increasing mortality risk. Early and accurate detection of PD progression is vital for effective management and improved patient outcomes. Current diagnostic methods, however, are often costly, time-consuming, and require specialized equipment and expertise. This work proposes an innovative approach to predicting PD progression using regression methods, Long Short-Term Memory (LSTM) networks, and Kolmogorov Arnold Networks (KAN). KAN, utilizing spline-parametrized univariate functions, allows for dynamic learning of activation patterns, unlike traditional linear models. The Movement Disorder Society-Sponsored Revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS) is a comprehensive tool for evaluating PD symptoms and is commonly used to measure disease progression. Additionally, protein or peptide abnormalities are linked to PD onset and progression. Identifying these associations can aid in predicting disease progression and understanding molecular changes. Comparing multiple models, including LSTM and KAN, this study aims to identify the method that delivers the highest metrics. The analysis reveals that KAN, with its dynamic learning capabilities, outperforms other approaches in predicting PD progression. This research highlights the potential of AI and machine learning in healthcare, paving the way for advanced computational models to enhance clinical predictions and improve patient care and treatment strategies in PD management.

2025

January

Predicting Crack Nucleation and Propagation in Brittle Materials Using Deep Operator Networks with Diverse Trunk Architectures

Authors: Elham Kiyani, Manav Manav, Nikhil Kadivar, Laura De Lorenzis, George Em Karniadakis

Venue: Computer Methods in Applied Mechanics and Engineering

Citation Count: 3

Abstract: Phase-field modeling reformulates fracture problems as energy minimization problems and enables a comprehensive characterization of the fracture process, including crack nucleation, propagation, merging, and branching, without relying on ad-hoc assumptions. However, the numerical solution of phase-field fracture problems is characterized by a high computational cost. To address this challenge, in this paper, we employ a deep neural operator (DeepONet) consisting of a branch network and a trunk network to solve brittle fracture problems. We explore three distinct approaches that vary in their trunk network configurations. In the first approach, we demonstrate the effectiveness of a two-step DeepONet, which results in a simplification of the learning task. In the second approach, we employ a physics-informed DeepONet, whereby the mathematical expression of the energy is integrated into the trunk network’s loss to enforce physical consistency. The integration of physics also results in a substantially smaller data size needed for training. In the third approach, we replace the neural network in the trunk with a Kolmogorov-Arnold Network and train it without the physics loss. Using these methods, we model crack nucleation in a one-dimensional homogeneous bar under prescribed end displacements, as well as crack propagation and branching in single edge-notched specimens with varying notch lengths subjected to tensile and shear loading. We show that the networks predict the solution fields accurately, and the error in the predicted fields is localized near the crack.

KAE: Kolmogorov-Arnold Auto-Encoder for Representation Learning

Authors: Fangchen Yu, Ruilizhen Hu, Yidong Lin, Yuqi Ma, Zhenghao Huang, Wenye Li

Abstract: The Kolmogorov-Arnold Network (KAN) has recently gained attention as an alternative to traditional multi-layer perceptrons (MLPs), offering improved accuracy and interpretability by employing learnable activation functions on edges. In this paper, we introduce the Kolmogorov-Arnold Auto-Encoder (KAE), which integrates KAN with autoencoders (AEs) to enhance representation learning for retrieval, classification, and denoising tasks. Leveraging the flexible polynomial functions in KAN layers, KAE captures complex data patterns and non-linear relationships. Experiments on benchmark datasets demonstrate that KAE improves latent representation quality, reduces reconstruction errors, and achieves superior performance in downstream tasks such as retrieval, classification, and denoising, compared to standard autoencoders and other KAN variants. These results suggest KAE’s potential as a useful tool for representation learning. Our code is available at \url{https://github.com/SciYu/KAE/}.

KAN KAN Buff Signed Graph Neural Networks?

Authors: Muhieddine Shebaro, Jelena Tešić

Abstract: Graph Representation Learning aims to create effective embeddings for nodes and edges that encapsulate their features and relationships. Graph Neural Networks (GNNs) leverage neural networks to model complex graph structures. Recently, the Kolmogorov-Arnold Neural Network (KAN) has emerged as a promising alternative to the traditional Multilayer Perceptron (MLP), offering improved accuracy and interpretability with fewer parameters. In this paper, we propose the integration of KANs into Signed Graph Convolutional Networks (SGCNs), leading to the development of KAN-enhanced SGCNs (KASGCN). We evaluate KASGCN on tasks such as signed community detection and link sign prediction to improve embedding quality in signed networks. Our experimental results indicate that KASGCN exhibits competitive or comparable performance to standard SGCNs across the tasks evaluated, with performance variability depending on the specific characteristics of the signed graph and the choice of parameter settings. These findings suggest that KASGCNs hold promise for enhancing signed graph analysis with context-dependent effectiveness.

EHCTNet: Enhanced Hybrid of CNN and Transformer Network for Remote Sensing Image Change Detection

Authors: Junjie Yang, Haibo Wan, Zhihai Shang

Citation Count: 1

Abstract: Remote sensing (RS) change detection incurs a high cost because of false negatives, which are more costly than false positives. Existing frameworks, struggling to improve the Precision metric to reduce the cost of false positive, still have limitations in focusing on the change of interest, which leads to missed detections and discontinuity issues. This work tackles these issues by enhancing feature learning capabilities and integrating the frequency components of feature information, with a strategy to incrementally boost the Recall value. We propose an enhanced hybrid of CNN and Transformer network (EHCTNet) for effectively mining the change information of interest. Firstly, a dual branch feature extraction module is used to extract the multi scale features of RS images. Secondly, the frequency component of these features is exploited by a refined module I. Thirdly, an enhanced token mining module based on the Kolmogorov Arnold Network is utilized to derive semantic information. Finally, the semantic change information’s frequency component, beneficial for final detection, is mined from the refined module II. Extensive experiments validate the effectiveness of EHCTNet in comprehending complex changes of interest. The visualization outcomes show that EHCTNet detects more intact and continuous changed areas and perceives more accurate neighboring distinction than state of the art models.

Improved Feature Extraction Network for Neuro-Oriented Target Speaker Extraction

Authors: Cunhang Fan, Youdian Gao, Zexu Pan, Jingjing Zhang, Hongyu Zhang, Jie Zhang, Zhao Lv

Venue: IEEE International Conference on Acoustics, Speech, and Signal Processing

Citation Count: 1

Abstract: The recent rapid development of auditory attention decoding (AAD) offers the possibility of using electroencephalography (EEG) as auxiliary information for target speaker extraction. However, effectively modeling long sequences of speech and resolving the identity of the target speaker from EEG signals remains a major challenge. In this paper, an improved feature extraction network (IFENet) is proposed for neuro-oriented target speaker extraction, which mainly consists of a speech encoder with dual-path Mamba and an EEG encoder with Kolmogorov-Arnold Networks (KAN). We propose SpeechBiMamba, which makes use of dual-path Mamba in modeling local and global speech sequences to extract speech features. In addition, we propose EEGKAN to effectively extract EEG features that are closely related to the auditory stimuli and locate the target speaker through the subject’s attention information. Experiments on the KUL and AVED datasets show that IFENet outperforms the state-of-the-art model, achieving 36\% and 29\% relative improvements in terms of scale-invariant signal-to-distortion ratio (SI-SDR) under an open evaluation condition.

KM-UNet KAN Mamba UNet for medical image segmentation

Author: Yibo Zhang

Abstract: Medical image segmentation is a critical task in medical imaging analysis. Traditional CNN-based methods struggle with modeling long-range dependencies, while Transformer-based models, despite their success, suffer from quadratic computational complexity. To address these limitations, we propose KM-UNet, a novel U-shaped network architecture that combines the strengths of Kolmogorov-Arnold Networks (KANs) and state-space models (SSMs). KM-UNet leverages the Kolmogorov-Arnold representation theorem for efficient feature representation and SSMs for scalable long-range modeling, achieving a balance between accuracy and computational efficiency. We evaluate KM-UNet on five benchmark datasets: ISIC17, ISIC18, CVC, BUSI, and GLAS. Experimental results demonstrate that KM-UNet achieves competitive performance compared to state-of-the-art methods in medical image segmentation tasks. To the best of our knowledge, KM-UNet is the first medical image segmentation framework integrating KANs and SSMs. This work provides a valuable baseline and new insights for the development of more efficient and interpretable medical image segmentation systems. The code is open source at https://github.com/2760613195/KM_UNet Keywords:KAN,Manba, state-space models,UNet, Medical image segmentation, Deep learning

LWFNet: Coherent Doppler Wind Lidar-Based Network for Wind Field Retrieval

Authors: Ran Tao, Chong Wang, Hao Chen, Mingjiao Jia, Xiang Shang, Luoyuan Qu, Guoliang Shentu, Yanyu Lu, Yanfeng Huo, Lei Bai, Xianghui Xue, Xiankang Dou

Abstract: Accurate detection of wind fields within the troposphere is essential for atmospheric dynamics research and plays a crucial role in extreme weather forecasting. Coherent Doppler wind lidar (CDWL) is widely regarded as the most suitable technique for high spatial and temporal resolution wind field detection. However, since coherent detection relies heavily on the concentration of aerosol particles, which cause Mie scattering, the received backscattering lidar signal exhibits significantly low intensity at high altitudes. As a result, conventional methods, such as spectral centroid estimation, often fail to produce credible and accurate wind retrieval results in these regions. To address this issue, we propose LWFNet, the first Lidar-based Wind Field (WF) retrieval neural Network, built upon Transformer and the Kolmogorov-Arnold network. Our model is trained solely on targets derived from the traditional wind retrieval algorithm and utilizes radiosonde measurements as the ground truth for test results evaluation. Experimental results demonstrate that LWFNet not only extends the maximum wind field detection range but also produces more accurate results, exhibiting a level of precision that surpasses the labeled targets. This phenomenon, which we refer to as super-accuracy, is explored by investigating the potential underlying factors that contribute to this intriguing occurrence. In addition, we compare the performance of LWFNet with other state-of-the-art (SOTA) models, highlighting its superior effectiveness and capability in high-resolution wind retrieval. LWFNet demonstrates remarkable performance in lidar-based wind field retrieval, setting a benchmark for future research and advancing the development of deep learning models in this domain.

Scaled-cPIKANs: Domain Scaling in Chebyshev-based Physics-informed Kolmogorov-Arnold Networks

Authors: Farinaz Mostajeran, Salah A Faroughi

Citation Count: 1

Abstract: Partial Differential Equations (PDEs) are integral to modeling many scientific and engineering problems. Physics-informed Neural Networks (PINNs) have emerged as promising tools for solving PDEs by embedding governing equations into the neural network loss function. However, when dealing with PDEs characterized by strong oscillatory dynamics over large computational domains, PINNs based on Multilayer Perceptrons (MLPs) often exhibit poor convergence and reduced accuracy. To address these challenges, this paper introduces Scaled-cPIKAN, a physics-informed architecture rooted in Kolmogorov-Arnold Networks (KANs). Scaled-cPIKAN integrates Chebyshev polynomial representations with a domain scaling approach that transforms spatial variables in PDEs into the standardized domain ([-1,1]^d), as intrinsically required by Chebyshev polynomials. By combining the flexibility of Chebyshev-based KANs (cKANs) with the physics-driven principles of PINNs, and the spatial domain transformation, Scaled-cPIKAN enables efficient representation of oscillatory dynamics across extended spatial domains while improving computational performance. We demonstrate Scaled-cPIKAN efficacy using four benchmark problems: the diffusion equation, the Helmholtz equation, the Allen-Cahn equation, as well as both forward and inverse formulations of the reaction-diffusion equation (with and without noisy data). Our results show that Scaled-cPIKAN significantly outperforms existing methods in all test cases. In particular, it achieves several orders of magnitude higher accuracy and faster convergence rate, making it a highly efficient tool for approximating PDE solutions that feature oscillatory behavior over large spatial domains.

Distance-Aware Error for Spline Networks: A Bottom-Up Approach to Uncertainty

Authors: Masoud Ataei, Mohammad Javad Khojasteh, Vikas Dhiman

Venue: IEEE International Conference on Acoustics, Speech, and Signal Processing

Abstract: We develop a new class of distance-aware error bounds that tightly characterize the approximation error of spline neural networks. Our bottom-up approach analyzes the error bound of each neuron (a spline) and then extends it to the full network. We begin with error bounds for Newton’s polynomial, generalize them to arbitrary splines under higher-order Lipschitz continuity, and extend the result to function compositions, the core of deep networks such as Kolmogorov-Arnold networks. By analyzing error propagation through composed spline layers, we obtain error bounds for the entire network. These bounds are deterministic, do not rely on sampling or probabilistic assumptions, and hold under mild regularity conditions. We evaluate our method on object shape estimation from sparse laser scans and safe navigation in unstructured environments. Our method is faster than the Gaussian process and Monte Carlo approaches, and our bounds reliably enclose the true error. We also develop a metric for the distance-awareness of an uncertainty estimator and show that distance-aware uncertainty for Kolmogorov networks (DAREK) is distance-aware in more regions than the baselines.

Interpretable deep learning illuminates multiple structures fluorescence imaging: a path toward trustworthy artificial intelligence in microscopy

Authors: Mingyang Chen, Luhong Jin, Xuwei Xuan, Defu Yang, Yun Cheng, Ju Zhang

Abstract: Live-cell imaging of multiple subcellular structures is essential for understanding subcellular dynamics. However, the conventional multi-color sequential fluorescence microscopy suffers from significant imaging delays and limited number of subcellular structure separate labeling, resulting in substantial limitations for real-time live-cell research applications. Here, we present the Adaptive Explainable Multi-Structure Network (AEMS-Net), a deep-learning framework that enables simultaneous prediction of two subcellular structures from a single image. The model normalizes staining intensity and prioritizes critical image features by integrating attention mechanisms and brightness adaptation layers. Leveraging the Kolmogorov-Arnold representation theorem, our model decomposes learned features into interpretable univariate functions, enhancing the explainability of complex subcellular morphologies. We demonstrate that AEMS-Net allows real-time recording of interactions between mitochondria and microtubules, requiring only half the conventional sequential-channel imaging procedures. Notably, this approach achieves over 30% improvement in imaging quality compared to traditional deep learning methods, establishing a new paradigm for long-term, interpretable live-cell imaging that advances the ability to explore subcellular dynamics.

Nonlinear port-Hamiltonian system identification from input-state-output data

Authors: Karim Cherifi, Achraf El Messaoudi, Hannes Gernandt, Marco Roschkowski

Abstract: A framework for identifying nonlinear port-Hamiltonian systems using input-state-output data is introduced. The framework utilizes neural networks’ universal approximation capacity to effectively represent complex dynamics in a structured way. We show that using the structure helps to make long-term predictions compared to baselines that do not incorporate physics. We also explore different architectures based on MLPs, KANs, and using prior information. The technique is validated through examples featuring nonlinearities in either the skew-symmetric terms, the dissipative terms, or the Hamiltonian.

Kolmogorov-Arnold networks for metal surface defect classification

Authors: Maciej Krzywda, Mariusz Wermiński, Szymon Łukasik, Amir H. Gandomi

Abstract: This paper presents the application of Kolmogorov-Arnold Networks (KAN) in classifying metal surface defects. Specifically, steel surfaces are analyzed to detect defects such as cracks, inclusions, patches, pitted surfaces, and scratches. Drawing on the Kolmogorov-Arnold theorem, KAN provides a novel approach compared to conventional multilayer perceptrons (MLPs), facilitating more efficient function approximation by utilizing spline functions. The results show that KAN networks can achieve better accuracy than convolutional neural networks (CNNs) with fewer parameters, resulting in faster convergence and improved performance in image classification.

Kolmogorov-Arnold Recurrent Network for Short Term Load Forecasting Across Diverse Consumers

Authors: Muhammad Umair Danish, Katarina Grolinger

Venue: Energy Reports

Citation Count: 7

Abstract: Load forecasting plays a crucial role in energy management, directly impacting grid stability, operational efficiency, cost reduction, and environmental sustainability. Traditional Vanilla Recurrent Neural Networks (RNNs) face issues such as vanishing and exploding gradients, whereas sophisticated RNNs such as LSTMs have shown considerable success in this domain. However, these models often struggle to accurately capture complex and sudden variations in energy consumption, and their applicability is typically limited to specific consumer types, such as offices or schools. To address these challenges, this paper proposes the Kolmogorov-Arnold Recurrent Network (KARN), a novel load forecasting approach that combines the flexibility of Kolmogorov-Arnold Networks with RNN’s temporal modeling capabilities. KARN utilizes learnable temporal spline functions and edge-based activations to better model non-linear relationships in load data, making it adaptable across a diverse range of consumer types. The proposed KARN model was rigorously evaluated on a variety of real-world datasets, including student residences, detached homes, a home with electric vehicle charging, a townhouse, and industrial buildings. Across all these consumer categories, KARN consistently outperformed traditional Vanilla RNNs, while it surpassed LSTM and Gated Recurrent Units (GRUs) in six buildings. The results demonstrate KARN’s superior accuracy and applicability, making it a promising tool for enhancing load forecasting in diverse energy management scenarios.

UNetVL: Enhancing 3D Medical Image Segmentation with Chebyshev KAN Powered Vision-LSTM

Authors: Xuhui Guo, Tanmoy Dam, Rohan Dhamdhere, Gourav Modanwal, Anant Madabhushi

Venue: IEEE International Symposium on Biomedical Imaging

Abstract: 3D medical image segmentation has progressed considerably due to Convolutional Neural Networks (CNNs) and Vision Transformers (ViTs), yet these methods struggle to balance long-range dependency acquisition with computational efficiency. To address this challenge, we propose UNETVL (U-Net Vision-LSTM), a novel architecture that leverages recent advancements in temporal information processing. UNETVL incorporates Vision-LSTM (ViL) for improved scalability and memory functions, alongside an efficient Chebyshev Kolmogorov-Arnold Networks (KAN) to handle complex and long-range dependency patterns more effectively. We validated our method on the ACDC and AMOS2022 (post challenge Task 2) benchmark datasets, showing a significant improvement in mean Dice score compared to recent state-of-the-art approaches, especially over its predecessor, UNETR, with increases of 7.3% on ACDC and 15.6% on AMOS, respectively. Extensive ablation studies were conducted to demonstrate the impact of each component in UNETVL, providing a comprehensive understanding of its architecture. Our code is available at https://github.com/tgrex6/UNETVL, facilitating further research and applications in this domain.

PRKAN: Parameter-Reduced Kolmogorov-Arnold Networks

Authors: Hoang-Thang Ta, Duy-Quy Thai, Anh Tran, Grigori Sidorov, Alexander Gelbukh

Citation Count: 2

Abstract: Kolmogorov-Arnold Networks (KANs) represent an innovation in neural network architectures, offering a compelling alternative to Multi-Layer Perceptrons (MLPs) in models such as Convolutional Neural Networks (CNNs), Recurrent Neural Networks (RNNs), and Transformers. By advancing network design, KANs drive groundbreaking research and enable transformative applications across various scientific domains involving neural networks. However, existing KANs often require significantly more parameters in their network layers than MLPs. To address this limitation, this paper introduces PRKANs (Parameter-Reduced Kolmogorov-Arnold Networks), which employ several methods to reduce the parameter count in KAN layers, making them comparable to MLP layers. Experimental results on the MNIST and Fashion-MNIST datasets demonstrate that PRKANs outperform several existing KANs, and their variant with attention mechanisms rivals the performance of MLPs, albeit with slightly longer training times. Furthermore, the study highlights the advantages of Gaussian Radial Basis Functions (GRBFs) and layer normalization in KAN designs. The repository for this work is available at: https://github.com/hoangthangta/All-KAN.

Kolmogorov-Arnold Network for Remote Sensing Image Semantic Segmentation

Authors: Xianping Ma, Ziyao Wang, Yin Hu, Xiaokang Zhang, Man-On Pun

Abstract: Semantic segmentation plays a crucial role in remote sensing applications, where the accurate extraction and representation of features are essential for high-quality results. Despite the widespread use of encoder-decoder architectures, existing methods often struggle with fully utilizing the high-dimensional features extracted by the encoder and efficiently recovering detailed information during decoding. To address these problems, we propose a novel semantic segmentation network, namely DeepKANSeg, including two key innovations based on the emerging Kolmogorov Arnold Network (KAN). Notably, the advantage of KAN lies in its ability to decompose high-dimensional complex functions into univariate transformations, enabling efficient and flexible representation of intricate relationships in data. First, we introduce a KAN-based deep feature refinement module, namely DeepKAN to effectively capture complex spatial and rich semantic relationships from high-dimensional features. Second, we replace the traditional multi-layer perceptron (MLP) layers in the global-local combined decoder with KAN-based linear layers, namely GLKAN. This module enhances the decoder’s ability to capture fine-grained details during decoding. To evaluate the effectiveness of the proposed method, experiments are conducted on two well-known fine-resolution remote sensing benchmark datasets, namely ISPRS Vaihingen and ISPRS Potsdam. The results demonstrate that the KAN-enhanced segmentation model achieves superior performance in terms of accuracy compared to state-of-the-art methods. They highlight the potential of KANs as a powerful alternative to traditional architectures in semantic segmentation tasks. Moreover, the explicit univariate decomposition provides improved interpretability, which is particularly beneficial for applications requiring explainable learning in remote sensing.

Kolmogorov-Arnold Networks and Evolutionary Game Theory for More Personalized Cancer Treatment

Authors: Sepinoud Azimi, Louise Spekking, Kateřina Staňková

Citation Count: 1

Abstract: Personalized cancer treatment is revolutionizing oncology by leveraging precision medicine and advanced computational techniques to tailor therapies to individual patients. Despite its transformative potential, challenges such as limited generalizability, interpretability, and reproducibility of predictive models hinder its integration into clinical practice. Current methodologies often rely on black-box machine learning models, which, while accurate, lack the transparency needed for clinician trust and real-world application. This paper proposes the development of an innovative framework that bridges Kolmogorov-Arnold Networks (KANs) and Evolutionary Game Theory (EGT) to address these limitations. Inspired by the Kolmogorov-Arnold representation theorem, KANs offer interpretable, edge-based neural architectures capable of modeling complex biological systems with unprecedented adaptability. Their integration into the EGT framework enables dynamic modeling of cancer progression and treatment responses. By combining KAN’s computational precision with EGT’s mechanistic insights, this hybrid approach promises to enhance predictive accuracy, scalability, and clinical usability.

Scalable Bayesian Physics-Informed Kolmogorov-Arnold Networks

Authors: Zhiwei Gao, George Em Karniadakis

Citation Count: 1

Abstract: Uncertainty quantification (UQ) plays a pivotal role in scientific machine learning, especially when surrogate models are used to approximate complex systems. Although multilayer perceptions (MLPs) are commonly employed as surrogates, they often suffer from overfitting due to their large number of parameters. Kolmogorov-Arnold networks (KANs) offer an alternative solution with fewer parameters. However, gradient-based inference methods, such as Hamiltonian Monte Carlo (HMC), may result in computational inefficiency when applied to KANs, especially for large-scale datasets, due to the high cost of back-propagation. To address these challenges, we propose a novel approach, combining the dropout Tikhonov ensemble Kalman inversion (DTEKI) with Chebyshev KANs. This gradient-free method effectively mitigates overfitting and enhances numerical stability. Additionally, we incorporate the active subspace method to reduce the parameter-space dimensionality, allowing us to improve the accuracy of predictions and obtain more reliable uncertainty estimates. Extensive experiments demonstrate the efficacy of our approach in various test cases, including scenarios with large datasets and high noise levels. Our results show that the new method achieves comparable or better accuracy, much higher efficiency as well as stability compared to HMC, in addition to scalability. Moreover, by leveraging the low-dimensional parameter subspace, our method preserves prediction accuracy while substantially reducing further the computational cost.

Kolmogorov-Arnold Networks for Time Series Granger Causality Inference

Authors: Meiliang Liu, Yunfang Xu, Zijin Li, Zhengye Si, Xiaoxiao Yang, Xinyue Yang, Zhiwen Zhao

Abstract: We propose the Granger causality inference Kolmogorov-Arnold Networks (KANGCI), a novel architecture that extends the recently proposed Kolmogorov-Arnold Networks (KAN) to the domain of causal inference. By extracting base weights from KAN layers and incorporating the sparsity-inducing penalty and ridge regularization, KANGCI effectively infers the Granger causality from time series. Additionally, we propose an algorithm based on time-reversed Granger causality that automatically selects causal relationships with better inference performance from the original or time-reversed time series or integrates the results to mitigate spurious connectivities. Comprehensive experiments conducted on Lorenz-96, Gene regulatory networks, fMRI BOLD signals, VAR, and real-world EEG datasets demonstrate that the proposed model achieves competitive performance to state-of-the-art methods in inferring Granger causality from nonlinear, high-dimensional, and limited-sample time series.

Free-Knots Kolmogorov-Arnold Network: On the Analysis of Spline Knots and Advancing Stability

Authors: Liangwewi Nathan Zheng, Wei Emma Zhang, Lin Yue, Miao Xu, Olaf Maennel, Weitong Chen

Citation Count: 2

Abstract: Kolmogorov-Arnold Neural Networks (KANs) have gained significant attention in the machine learning community. However, their implementation often suffers from poor training stability and heavy trainable parameter. Furthermore, there is limited understanding of the behavior of the learned activation functions derived from B-splines. In this work, we analyze the behavior of KANs through the lens of spline knots and derive the lower and upper bound for the number of knots in B-spline-based KANs. To address existing limitations, we propose a novel Free Knots KAN that enhances the performance of the original KAN while reducing the number of trainable parameters to match the trainable parameter scale of standard Multi-Layer Perceptrons (MLPs). Additionally, we introduce new a training strategy to ensure $C^2$ continuity of the learnable spline, resulting in smoother activation compared to the original KAN and improve the training stability by range expansion. The proposed method is comprehensively evaluated on 8 datasets spanning various domains, including image, text, time series, multimodal, and function approximation tasks. The promising results demonstrates the feasibility of KAN-based network and the effectiveness of proposed method.

Adversarial-Ensemble Kolmogorov Arnold Networks for Enhancing Indoor Wi-Fi Positioning: A Defensive Approach Against Spoofing and Signal Manipulation Attacks

Authors: Mitul Goswami, Romit Chatterjee, Somnath Mahato, Prasant Kumar Pattnaik

Abstract: The research presents a study on enhancing the robustness of Wi-Fi-based indoor positioning systems against adversarial attacks. The goal is to improve the positioning accuracy and resilience of these systems under two attack scenarios: Wi-Fi Spoofing and Signal Strength Manipulation. Three models are developed and evaluated: a baseline model (M_Base), an adversarially trained robust model (M_Rob), and an ensemble model (M_Ens). All models utilize a Kolmogorov-Arnold Network (KAN) architecture. The robust model is trained with adversarially perturbed data, while the ensemble model combines predictions from both the base and robust models. Experimental results show that the robust model reduces positioning error by approximately 10% compared to the baseline, achieving 2.03 meters error under Wi-Fi spoofing and 2.00 meters under signal strength manipulation. The ensemble model further outperforms with errors of 2.01 meters and 1.975 meters for the respective attack types. This analysis highlights the effectiveness of adversarial training techniques in mitigating attack impacts. The findings underscore the importance of considering adversarial scenarios in developing indoor positioning systems, as improved resilience can significantly enhance the accuracy and reliability of such systems in mission-critical environments.

Boosting the Accuracy of Stock Market Prediction via Multi-Layer Hybrid MTL Structure

Author: Yuxi Hong

Venue: International Journal of Intelligent Decision Technologies

Abstract: Accurate stock market prediction provides great opportunities for informed decision-making, yet existing methods struggle with financial data’s non-linear, high-dimensional, and volatile characteristics. Advanced predictive models are needed to effectively address these complexities. This paper proposes a novel multi-layer hybrid multi-task learning (MTL) framework aimed at achieving more efficient stock market predictions. It involves a Transformer encoder to extract complex correspondences between various input features, a Bidirectional Gated Recurrent Unit (BiGRU) to capture long-term temporal relationships, and a Kolmogorov-Arnold Network (KAN) to enhance the learning process. Experimental evaluations indicate that the proposed learning structure achieves great performance, with an MAE as low as 1.078, a MAPE as low as 0.012, and an R^2 as high as 0.98, when compared with other competitive networks.

KAA: Kolmogorov-Arnold Attention for Enhancing Attentive Graph Neural Networks

Authors: Taoran Fang, Tianhong Gao, Chunping Wang, Yihao Shang, Wei Chow, Lei Chen, Yang Yang

Venue: International Conference on Learning Representations

Citation Count: 2

Abstract: Graph neural networks (GNNs) with attention mechanisms, often referred to as attentive GNNs, have emerged as a prominent paradigm in advanced GNN models in recent years. However, our understanding of the critical process of scoring neighbor nodes remains limited, leading to the underperformance of many existing attentive GNNs. In this paper, we unify the scoring functions of current attentive GNNs and propose Kolmogorov-Arnold Attention (KAA), which integrates the Kolmogorov-Arnold Network (KAN) architecture into the scoring process. KAA enhances the performance of scoring functions across the board and can be applied to nearly all existing attentive GNNs. To compare the expressive power of KAA with other scoring functions, we introduce Maximum Ranking Distance (MRD) to quantitatively estimate their upper bounds in ranking errors for node importance. Our analysis reveals that, under limited parameters and constraints on width and depth, both linear transformation-based and MLP-based scoring functions exhibit finite expressive power. In contrast, our proposed KAA, even with a single-layer KAN parameterized by zero-order B-spline functions, demonstrates nearly infinite expressive power. Extensive experiments on both node-level and graph-level tasks using various backbone models show that KAA-enhanced scoring functions consistently outperform their original counterparts, achieving performance improvements of over 20% in some cases.

Local Control Networks (LCNs): Optimizing Flexibility in Neural Network Data Pattern Capture

Authors: Hy Nguyen, Duy Khoa Pham, Srikanth Thudumu, Hung Du, Rajesh Vasa, Kon Mouzakis

Abstract: The widespread use of Multi-layer perceptrons (MLPs) often relies on a fixed activation function (e.g., ReLU, Sigmoid, Tanh) for all nodes within the hidden layers. While effective in many scenarios, this uniformity may limit the networks ability to capture complex data patterns. We argue that employing the same activation function at every node is suboptimal and propose leveraging different activation functions at each node to increase flexibility and adaptability. To achieve this, we introduce Local Control Networks (LCNs), which leverage B-spline functions to enable distinct activation curves at each node. Our mathematical analysis demonstrates the properties and benefits of LCNs over conventional MLPs. In addition, we demonstrate that more complex architectures, such as Kolmogorov-Arnold Networks (KANs), are unnecessary in certain scenarios, and LCNs can be a more efficient alternative. Empirical experiments on various benchmarks and datasets validate our theoretical findings. In computer vision tasks, LCNs achieve marginal improvements over MLPs and outperform KANs by approximately 5\%, while also being more computationally efficient than KANs. In basic machine learning tasks, LCNs show a 1\% improvement over MLPs and a 0.6\% improvement over KANs. For symbolic formula representation tasks, LCNs perform on par with KANs, with both architectures outperforming MLPs. Our findings suggest that diverse activations at the node level can lead to improved performance and efficiency.

Kolmogorov Arnold Neural Interpolator for Downscaling and Correcting Meteorological Fields from In-Situ Observations

Authors: Zili Liu, Hao Chen, Lei Bai, Wenyuan Li, Zhengxia Zou, Zhenwei Shi

Citation Count: 2

Abstract: Obtaining accurate weather forecasts at station locations is a critical challenge due to systematic biases arising from the mismatch between multi-scale, continuous atmospheric characteristic and their discrete, gridded representations. Previous works have primarily focused on modeling gridded meteorological data, inherently neglecting the off-grid, continuous nature of atmospheric states and leaving such biases unresolved. To address this, we propose the Kolmogorov Arnold Neural Interpolator (KANI), a novel framework that redefines meteorological field representation as continuous neural functions derived from discretized grids. Grounded in the Kolmogorov Arnold theorem, KANI captures the inherent continuity of atmospheric states and leverages sparse in-situ observations to correct these biases systematically. Furthermore, KANI introduces an innovative zero-shot downscaling capability, guided by high-resolution topographic textures without requiring high-resolution meteorological fields for supervision. Experimental results across three sub-regions of the continental United States indicate that KANI achieves an accuracy improvement of 40.28% for temperature and 67.41% for wind speed, highlighting its significant improvement over traditional interpolation methods. This enables continuous neural representation of meteorological variables through neural networks, transcending the limitations of conventional grid-based representations.

Discovering Dynamics with Kolmogorov Arnold Networks: Linear Multistep Method-Based Algorithms and Error Estimation

Authors: Jintao Hu, Hongjiong Tian, Qian Guo

Abstract: Uncovering the underlying dynamics from observed data is a critical task in various scientific fields. Recent advances have shown that combining deep learning techniques with linear multistep methods (LMMs) can be highly effective for this purpose. In this work, we propose a novel framework that integrates Kolmogorov Arnold Networks (KANs) with LMMs for the discovery and approximation of dynamical systems’ vector fields. Specifically, we begin by establishing precise error bounds for two-layer B-spline KANs when approximating the governing functions of dynamical systems. Leveraging the approximation capabilities of KANs, we demonstrate that for certain families of LMMs, the total error is constrained within a specific range that accounts for both the method’s step size and the network’s approximation accuracy. Additionally, we analyze the difference between the numerical solution obtained from solving the ordinary differential equations with the fitted vector fields and the true solution of the dynamical system. To validate our theoretical results, we provide several numerical examples that highlight the effectiveness of our approach.

Efficiency Bottlenecks of Convolutional Kolmogorov-Arnold Networks: A Comprehensive Scrutiny with ImageNet, AlexNet, LeNet and Tabular Classification

Authors: Ashim Dahal, Saydul Akbar Murad, Nick Rahimi

Abstract: Algorithmic level developments like Convolutional Neural Networks, transformers, attention mechanism, Retrieval Augmented Generation and so on have changed Artificial Intelligence. Recent such development was observed by Kolmogorov-Arnold Networks that suggested to challenge the fundamental concept of a Neural Network, thus change Multilayer Perceptron, and Convolutional Neural Networks. They received a good reception in terms of scientific modeling, yet had some drawbacks in terms of efficiency. In this paper, we train Convolutional Kolmogorov Arnold Networks (CKANs) with the ImageNet-1k dataset with 1.3 million images, MNIST dataset with 60k images and a tabular biological science related MoA dataset and test the promise of CKANs in terms of FLOPS, Inference Time, number of trainable parameters and training time against the accuracy, precision, recall and f-1 score they produce against the standard industry practice on CNN models. We show that the CKANs perform fair yet slower than CNNs in small size dataset like MoA and MNIST but are not nearly comparable as the dataset gets larger and more complex like the ImageNet. The code implementation of this paper can be found on the link: https://github.com/ashimdahal/Study-of-Convolutional-Kolmogorov-Arnold-networks △ Less

Optimizing the Optimizer for Physics-Informed Neural Networks and Kolmogorov-Arnold Networks

Authors: Elham Kiyani, Khemraj Shukla, Jorge F. Urbán, Jérôme Darbon, George Em Karniadakis

Citation Count: 7

Abstract: Physics-Informed Neural Networks (PINNs) have revolutionized the computation of PDE solutions by integrating partial differential equations (PDEs) into the neural network’s training process as soft constraints, becoming an important component of the scientific machine learning (SciML) ecosystem. More recently, physics-informed Kolmogorv-Arnold networks (PIKANs) have also shown to be effective and comparable in accuracy with PINNs. In their current implementation, both PINNs and PIKANs are mainly optimized using first-order methods like Adam, as well as quasi-Newton methods such as BFGS and its low-memory variant, L-BFGS. However, these optimizers often struggle with highly non-linear and non-convex loss landscapes, leading to challenges such as slow convergence, local minima entrapment, and (non)degenerate saddle points. In this study, we investigate the performance of Self-Scaled BFGS (SSBFGS), Self-Scaled Broyden (SSBroyden) methods and other advanced quasi-Newton schemes, including BFGS and L-BFGS with different line search strategies. These methods dynamically rescale updates based on historical gradient information, thus enhancing training efficiency and accuracy. We systematically compare these optimizers using both PINNs and PIKANs on key challenging PDEs, including the Burgers, Allen-Cahn, Kuramoto-Sivashinsky, Ginzburg-Landau, and Stokes equations. Additionally, we evaluate the performance of SSBFGS and SSBroyden for Deep Operator Network (DeepONet) architectures, demonstrating their effectiveness for data-driven operator learning. Our findings provide state-of-the-art results with orders-of-magnitude accuracy improvements without the use of adaptive weights or any other enhancements typically employed in PINNs.

RAINER: A Robust Ensemble Learning Grid Search-Tuned Framework for Rainfall Patterns Prediction

Authors: Zhenqi Li, Junhao Zhong, Hewei Wang, Jinfeng Xu, Yijie Li, Jinjiang You, Jiayi Zhang, Runzhi Wu, Soumyabrata Dev

Abstract: Rainfall prediction remains a persistent challenge due to the highly nonlinear and complex nature of meteorological data. Existing approaches lack systematic utilization of grid search for optimal hyperparameter tuning, relying instead on heuristic or manual selection, frequently resulting in sub-optimal results. Additionally, these methods rarely incorporate newly constructed meteorological features such as differences between temperature and humidity to capture critical weather dynamics. Furthermore, there is a lack of systematic evaluation of ensemble learning techniques and limited exploration of diverse advanced models introduced in the past one or two years. To address these limitations, we propose a robust ensemble learning grid search-tuned framework (RAINER) for rainfall prediction. RAINER incorporates a comprehensive feature engineering pipeline, including outlier removal, imputation of missing values, feature reconstruction, and dimensionality reduction via Principal Component Analysis (PCA). The framework integrates novel meteorological features to capture dynamic weather patterns and systematically evaluates non-learning mathematical-based methods and a variety of machine learning models, from weak classifiers to advanced neural networks such as Kolmogorov-Arnold Networks (KAN). By leveraging grid search for hyperparameter tuning and ensemble voting techniques, RAINER achieves promising results within real-world datasets.

A Genetic Algorithm-Based Approach for Automated Optimization of Kolmogorov-Arnold Networks in Classification Tasks

Authors: Quan Long, Bin Wang, Bing Xue, Mengjie Zhang

Abstract: To address the issue of interpretability in multilayer perceptrons (MLPs), Kolmogorov-Arnold Networks (KANs) are introduced in 2024. However, optimizing KAN structures is labor-intensive, typically requiring manual intervention and parameter tuning. This paper proposes GA-KAN, a genetic algorithm-based approach that automates the optimization of KANs, requiring no human intervention in the design process. To the best of our knowledge, this is the first time that evolutionary computation is explored to optimize KANs automatically. Furthermore, inspired by the use of sparse connectivity in MLPs in effectively reducing the number of parameters, GA-KAN further explores sparse connectivity to tackle the challenge of extensive parameter spaces in KANs. GA-KAN is validated on two toy datasets, achieving optimal results without the manual tuning required by the original KAN. Additionally, GA-KAN demonstrates superior performance across five classification datasets, outperforming traditional methods on all datasets and providing interpretable symbolic formulae for the Wine and Iris datasets, thereby enhancing model transparency. Furthermore, GA-KAN significantly reduces the number of parameters over the standard KAN across all the five datasets. The core contributions of GA-KAN include automated optimization, a new encoding strategy, and a new decoding process, which together improve the accuracy and interpretability, and reduce the number of parameters.

Assessment of the January 2025 Los Angeles County wildfires: A multi-modal analysis of impact, response, and population exposure

Author: Seyd Teymoor Seydi

Abstract: This study presents a comprehensive analysis of four significant California wildfires: Palisades, Eaton, Kenneth, and Hurst, examining their impacts through multiple dimensions, including land cover change, jurisdictional management, structural damage, and demographic vulnerability. Using the Chebyshev-Kolmogorov-Arnold network model applied to Sentinel-2 imagery, the extent of burned areas was mapped, ranging from 315.36 to 10,960.98 hectares. Our analysis revealed that shrubland ecosystems were consistently the most affected, comprising 57.4-75.8% of burned areas across all events. The jurisdictional assessment demonstrated varying management complexities, from singular authority (98.7% in the Palisades Fire) to distributed management across multiple agencies. A structural impact analysis revealed significant disparities between urban interface fires (Eaton: 9,869 structures; Palisades: 8,436 structures) and rural events (Kenneth: 24 structures; Hurst: 17 structures). The demographic analysis showed consistent gender distributions, with 50.9% of the population identified as female and 49.1% as male. Working-age populations made up the majority of the affected populations, ranging from 53.7% to 54.1%, with notable temporal shifts in post-fire periods. The study identified strong correlations between urban interface proximity, structural damage, and population exposure. The Palisades and Eaton fires affected over 20,000 people each, compared to fewer than 500 in rural events. These findings offer valuable insights for the development of targeted wildfire management strategies, particularly in wildland urban interface zones, and emphasize the need for age- and gender-conscious approaches in emergency response planning.

Explainable Machine Learning: An Illustration of Kolmogorov-Arnold Network Model for Airfoil Lift Prediction

Author: Sudhanva Kulkarni

Abstract: Data science has emerged as fourth paradigm of scientific exploration. However many machine learning models operate as black boxes offering limited insight into the reasoning behind their predictions. This lack of transparency is one of the drawbacks to generate new knowledge from data. Recently Kolmogorov-Arnold Network or KAN has been proposed as an alternative model which embeds explainable AI. This study demonstrates the potential of KAN for new scientific exploration. KAN along with five other popular supervised machine learning models are applied to the well-known problem of airfoil lift prediction in aerospace engineering. Standard data generated from an earlier study on 2900 different airfoils is used. KAN performed the best with an R2 score of 96.17 percent on the test data, surpassing both the baseline model and Multi Layer Perceptron. Explainability of KAN is shown by pruning and symbolizing the model resulting in an equation for coefficient of lift in terms of input variables. The explainable information retrieved from KAN model is found to be consistent with the known physics of lift generation by airfoil thus demonstrating its potential to aid in scientific exploration.

HKAN: Hierarchical Kolmogorov-Arnold Network without Backpropagation

Authors: Grzegorz Dudek, Tomasz Rodak

Abstract: This paper introduces the Hierarchical Kolmogorov-Arnold Network (HKAN), a novel network architecture that offers a competitive alternative to the recently proposed Kolmogorov-Arnold Network (KAN). Unlike KAN, which relies on backpropagation, HKAN adopts a randomized learning approach, where the parameters of its basis functions are fixed, and linear aggregations are optimized using least-squares regression. HKAN utilizes a hierarchical multi-stacking framework, with each layer refining the predictions from the previous one by solving a series of linear regression problems. This non-iterative training method simplifies computation and eliminates sensitivity to local minima in the loss function. Empirical results show that HKAN delivers comparable, if not superior, accuracy and stability relative to KAN across various regression tasks, while also providing insights into variable importance. The proposed approach seamlessly integrates theoretical insights with practical applications, presenting a robust and efficient alternative for neural network modeling.

Enhancing Neural Function Approximation: The XNet Outperforming KAN

Authors: Xin Li, Xiaotao Zheng, Zhihong Xia

Citation Count: 2

Abstract: XNet is a single-layer neural network architecture that leverages Cauchy integral-based activation functions for high-order function approximation. Through theoretical analysis, we show that the Cauchy activation functions used in XNet can achieve arbitrary-order polynomial convergence, fundamentally outperforming traditional MLPs and Kolmogorov-Arnold Networks (KANs) that rely on increased depth or B-spline activations. Our extensive experiments on function approximation, PDE solving, and reinforcement learning demonstrate XNet’s superior performance - reducing approximation error by up to 50000 times and accelerating training by up to 10 times compared to existing approaches. These results establish XNet as a highly efficient architecture for both scientific computing and AI applications.

February

On the study of frequency control and spectral bias in Wavelet-Based Kolmogorov Arnold networks: A path to physics-informed KANs

Authors: Juan Daniel Meshir, Abel Palafox, Edgar Alejandro Guerrero

Citation Count: 4

Abstract: Spectral bias, the tendency of neural networks to prioritize learning low-frequency components of functions during the initial training stages, poses a significant challenge when approximating solutions with high-frequency details. This issue is particularly pronounced in physics-informed neural networks (PINNs), widely used to solve differential equations that describe physical phenomena. In the literature, contributions such as Wavelet Kolmogorov Arnold Networks (Wav-KANs) have demonstrated promising results in capturing both low- and high-frequency components. Similarly, Fourier features (FF) are often employed to address this challenge. However, the theoretical foundations of Wav-KANs, particularly the relationship between the frequency of the mother wavelet and spectral bias, remain underexplored. A more in-depth understanding of how Wav-KANs manage high-frequency terms could offer valuable insights for addressing oscillatory phenomena encountered in parabolic, elliptic, and hyperbolic differential equations. In this work, we analyze the eigenvalues of the neural tangent kernel (NTK) of Wav-KANs to enhance their ability to converge on high-frequency components, effectively mitigating spectral bias. Our theoretical findings are validated through numerical experiments, where we also discuss the limitations of traditional approaches, such as standard PINNs and Fourier features, in addressing multi-frequency problems.

Forecasting VIX using interpretable Kolmogorov-Arnold networks

Authors: So-Yoon Cho, Sungchul Lee, Hyun-Gyoon Kim

Abstract: This paper presents the use of Kolmogorov-Arnold Networks (KANs) for forecasting the CBOE Volatility Index (VIX). Unlike traditional MLP-based neural networks that are often criticized for their black-box nature, KAN offers an interpretable approach via learnable spline-based activation functions and symbolification. Based on a parsimonious architecture with symbolic functions, KAN expresses a forecast of the VIX as a closed-form in terms of explanatory variables, and provide interpretable insights into key characteristics of the VIX, including mean reversion and the leverage effect. Through in-depth empirical analysis across multiple datasets and periods, we show that KANs achieve competitive forecasting performance while requiring significantly fewer parameters compared to MLP-based neural network models. Our findings demonstrate the capacity and potential of KAN as an interpretable financial time-series forecasting method.

Data-Efficient Model for Psychological Resilience Prediction based on Neurological Data

Authors: Zhi Zhang, Yan Liu, Mengxia Gao, Yu Yang, Jiannong Cao, Wai Kai Hou, Shirley Li, Sonata Yau, Yun Kwok Wing, Tatia M. C. Lee

Abstract: Psychological resilience, defined as the ability to rebound from adversity, is crucial for mental health. Compared with traditional resilience assessments through self-reported questionnaires, resilience assessments based on neurological data offer more objective results with biological markers, hence significantly enhancing credibility. This paper proposes a novel data-efficient model to address the scarcity of neurological data. We employ Neuro Kolmogorov-Arnold Networks as the structure of the prediction model. In the training stage, a new trait-informed multimodal representation algorithm with a smart chunk technique is proposed to learn the shared latent space with limited data. In the test stage, a new noise-informed inference algorithm is proposed to address the low signal-to-noise ratio of the neurological data. The proposed model not only shows impressive performance on both public datasets and self-constructed datasets but also provides some valuable psychological hypotheses for future research.

Function Approximation Using Analog Building Blocks in Flexible Electronics

Authors: Paula Carolina Lozano Duarte, Aradhana Dube, Georgios Zervakis, Mehdi Tahoori, Sani Nassif

Venue: IEEE International Symposium on Quality Electronic Design

Abstract: Function approximation is crucial in Flexible Electronics (FE), where applications demand efficient computational techniques within strict constraints on size, power, and performance. Devices like wearables and compact sensors are constrained by their limited physical dimensions and energy capacity, making traditional digital function approximation challenging and hardware-demanding. This paper addresses function approximation in FE by proposing a systematic and generic approach using a combination of Analog Building Blocks (ABBs) that perform basic mathematical operations such as addition, multiplication, and squaring. These ABBs serve as the foundation for constructing splines, which are then employed in the creation of Kolmogorov-Arnold Networks (KANs), improving the approximation. The analog realization of KAN offers a promising alternative to digital solutions, providing significant hardware benefits, particularly in terms of area and power consumption. Our design achieves a 125x reduction in area and a 10.59% power saving compared to a digital spline with 8-bit precision. Results also show that the analog design introduces an approximation error of up to 7.58% due to both the design and parasitic elements. Nevertheless, KANs are shown to be a viable candidate for function approximation in FE, with potential for further optimization to address the challenges of error reduction and hardware cost.

Efficient Denial of Service Attack Detection in IoT using Kolmogorov-Arnold Networks

Author: Oleksandr Kuznetsov

Abstract: The proliferation of Internet of Things (IoT) devices has created a pressing need for efficient security solutions, particularly against Denial of Service (DoS) attacks. While existing detection approaches demonstrate high accuracy, they often require substantial computational resources, making them impractical for IoT deployment. This paper introduces a novel lightweight approach to DoS attack detection based on Kolmogorov-Arnold Networks (KANs). By leveraging spline-based transformations instead of traditional weight matrices, our solution achieves state-of-the-art detection performance while maintaining minimal resource requirements. Experimental evaluation on the CICIDS2017 dataset demonstrates 99.0% detection accuracy with only 0.19 MB memory footprint and 2.00 ms inference time per sample. Compared to existing solutions, KAN reduces memory requirements by up to 98% while maintaining competitive detection rates. The model’s linear computational complexity ensures efficient scaling with input size, making it particularly suitable for large-scale IoT deployments. We provide comprehensive performance comparisons with recent approaches and demonstrate effectiveness across various DoS attack patterns. Our solution addresses the critical challenge of implementing sophisticated attack detection on resource-constrained devices, offering a practical approach to enhancing IoT security without compromising computational efficiency.

EFKAN: A KAN-Integrated Neural Operator For Efficient Magnetotelluric Forward Modeling

Authors: Feng Wang, Hong Qiu, Yingying Huang, Xiaozhe Gu, Renfang Wang, Bo Yang

Citation Count: 1

Abstract: Magnetotelluric (MT) forward modeling is fundamental for improving the accuracy and efficiency of MT inversion. Neural operators (NOs) have been effectively used for rapid MT forward modeling, demonstrating their promising performance in solving the MT forward modeling-related partial differential equations (PDEs). Particularly, they can obtain the electromagnetic field at arbitrary locations and frequencies. In these NOs, the projection layers have been dominated by multi-layer perceptrons (MLPs), which may potentially reduce the accuracy of solution due to they usually suffer from the disadvantages of MLPs, such as lack of interpretability, overfitting, and so on. Therefore, to improve the accuracy of MT forward modeling with NOs and explore the potential alternatives to MLPs, we propose a novel neural operator by extending the Fourier neural operator (FNO) with Kolmogorov-Arnold network (EFKAN). Within the EFKAN framework, the FNO serves as the branch network to calculate the apparent resistivity and phase from the resistivity model in the frequency domain. Meanwhile, the KAN acts as the trunk network to project the resistivity and phase, determined by the FNO, to the desired locations and frequencies. Experimental results demonstrate that the proposed method not only achieves higher accuracy in obtaining apparent resistivity and phase compared to the NO equipped with MLPs at the desired frequencies and locations but also outperforms traditional numerical methods in terms of computational speed.

CVKAN: Complex-Valued Kolmogorov-Arnold Networks

Authors: Matthias Wolff, Florian Eilers, Xiaoyi Jiang

Citation Count: 1

Abstract: In this work we propose CVKAN, a complex-valued Kolmogorov-Arnold Network (KAN), to join the intrinsic interpretability of KANs and the advantages of Complex-Valued Neural Networks (CVNNs). We show how to transfer a KAN and the necessary associated mechanisms into the complex domain. To confirm that CVKAN meets expectations we conduct experiments on symbolic complex-valued function fitting and physically meaningful formulae as well as on a more realistic dataset from knot theory. Our proposed CVKAN is more stable and performs on par or better than real-valued KANs while requiring less parameters and a shallower network architecture, making it more explainable.

Constitutive Kolmogorov-Arnold Networks (CKANs): Combining Accuracy and Interpretability in Data-Driven Material Modeling

Authors: Kian P. Abdolazizi, Roland C. Aydin, Christian J. Cyron, Kevin Linka

Citation Count: 3

Abstract: Hybrid constitutive modeling integrates two complementary approaches for describing and predicting a material’s mechanical behavior: purely data-driven black-box methods and physically constrained, theory-based models. While black-box methods offer high accuracy, they often lack interpretability and extrapolability. Conversely, physics-based models provide theoretical insight and generalizability but may not capture complex behaviors with the same accuracy. Traditionally, hybrid modeling has required a trade-off between these aspects. In this paper, we show how recent advances in symbolic machine learning, specifically Kolmogorov-Arnold Networks (KANs), help to overcome this limitation. We introduce Constitutive Kolmogorov-Arnold Networks (CKANs) as a new class of hybrid constitutive models. By incorporating a post-processing symbolification step, CKANs combine the predictive accuracy of data-driven models with the interpretability and extrapolation capabilities of symbolic expressions, bridging the gap between machine learning and physical modeling.

Kolmogorov-Arnold Fourier Networks

Authors: Jusheng Zhang, Yijia Fan, Kaitong Cai, Keze Wang

Abstract: Although Kolmogorov-Arnold based interpretable networks (KAN) have strong theoretical expressiveness, they face significant parameter explosion and high-frequency feature capture challenges in high-dimensional tasks. To address this issue, we propose the Kolmogorov-Arnold-Fourier Network (KAF), which effectively integrates trainable Random Fourier Features (RFF) and a novel hybrid GELU-Fourier activation mechanism to balance parameter efficiency and spectral representation capabilities. Our key technical contributions include: (1) merging KAN’s dual-matrix structure through matrix association properties to substantially reduce parameters; (2) introducing learnable RFF initialization strategies to eliminate spectral distortion in high-dimensional approximation tasks; (3) implementing an adaptive hybrid activation function that progressively enhances frequency representation during the training process. Comprehensive experiments demonstrate the superiority of our KAF across various domains including vision, NLP, audio processing, and differential equation-solving tasks, effectively combining theoretical interpretability with practical utility and computational efficiency.

Low Tensor-Rank Adaptation of Kolmogorov–Arnold Networks

Authors: Yihang Gao, Michael K. Ng, Vincent Y. F. Tan

Abstract: Kolmogorov–Arnold networks (KANs) have demonstrated their potential as an alternative to multi-layer perceptions (MLPs) in various domains, especially for science-related tasks. However, transfer learning of KANs remains a relatively unexplored area. In this paper, inspired by Tucker decomposition of tensors and evidence on the low tensor-rank structure in KAN parameter updates, we develop low tensor-rank adaptation (LoTRA) for fine-tuning KANs. We study the expressiveness of LoTRA based on Tucker decomposition approximations. Furthermore, we provide a theoretical analysis to select the learning rates for each LoTRA component to enable efficient training. Our analysis also shows that using identical learning rates across all components leads to inefficient training, highlighting the need for an adaptive learning rate strategy. Beyond theoretical insights, we explore the application of LoTRA for efficiently solving various partial differential equations (PDEs) by fine-tuning KANs. Additionally, we propose Slim KANs that incorporate the inherent low-tensor-rank properties of KAN parameter tensors to reduce model size while maintaining superior performance. Experimental results validate the efficacy of the proposed learning rate selection strategy and demonstrate the effectiveness of LoTRA for transfer learning of KANs in solving PDEs. Further evaluations on Slim KANs for function representation and image classification tasks highlight the expressiveness of LoTRA and the potential for parameter reduction through low tensor-rank decomposition.

TimeKAN: KAN-based Frequency Decomposition Learning Architecture for Long-term Time Series Forecasting

Authors: Songtao Huang, Zhen Zhao, Can Li, Lei Bai

Venue: International Conference on Learning Representations

Abstract: Real-world time series often have multiple frequency components that are intertwined with each other, making accurate time series forecasting challenging. Decomposing the mixed frequency components into multiple single frequency components is a natural choice. However, the information density of patterns varies across different frequencies, and employing a uniform modeling approach for different frequency components can lead to inaccurate characterization. To address this challenges, inspired by the flexibility of the recent Kolmogorov-Arnold Network (KAN), we propose a KAN-based Frequency Decomposition Learning architecture (TimeKAN) to address the complex forecasting challenges caused by multiple frequency mixtures. Specifically, TimeKAN mainly consists of three components: Cascaded Frequency Decomposition (CFD) blocks, Multi-order KAN Representation Learning (M-KAN) blocks and Frequency Mixing blocks. CFD blocks adopt a bottom-up cascading approach to obtain series representations for each frequency band. Benefiting from the high flexibility of KAN, we design a novel M-KAN block to learn and represent specific temporal patterns within each frequency band. Finally, Frequency Mixing blocks is used to recombine the frequency bands into the original format. Extensive experimental results across multiple real-world time series datasets demonstrate that TimeKAN achieves state-of-the-art performance as an extremely lightweight architecture. Code is available at https://github.com/huangst21/TimeKAN.

MatrixKAN: Parallelized Kolmogorov-Arnold Network

Authors: Cale Coffman, Lizhong Chen

Abstract: Kolmogorov-Arnold Networks (KAN) are a new class of neural network architecture representing a promising alternative to the Multilayer Perceptron (MLP), demonstrating improved expressiveness and interpretability. However, KANs suffer from slow training and inference speeds relative to MLPs due in part to the recursive nature of the underlying B-spline calculations. This issue is particularly apparent with respect to KANs utilizing high-degree B-splines, as the number of required non-parallelizable recursions is proportional to B-spline degree. We solve this issue by proposing MatrixKAN, a novel optimization that parallelizes B-spline calculations with matrix representation and operations, thus significantly improving effective computation time for models utilizing high-degree B-splines. In this paper, we demonstrate the superior scaling of MatrixKAN’s computation time relative to B-spline degree. Further, our experiments demonstrate speedups of approximately 40x relative to KAN, with significant additional speedup potential for larger datasets or higher spline degrees.

Unpaired Image Dehazing via Kolmogorov-Arnold Transformation of Latent Features

Author: Le-Anh Tran

Abstract: This paper proposes an innovative framework for Unsupervised Image Dehazing via Kolmogorov-Arnold Transformation, termed UID-KAT. Image dehazing is recognized as a challenging and ill-posed vision task that requires complex transformations and interpretations in the feature space. Recent advancements have introduced Kolmogorov-Arnold Networks (KANs), inspired by the Kolmogorov-Arnold representation theorem, as promising alternatives to Multi-Layer Perceptrons (MLPs) since KANs can leverage their polynomial foundation to more efficiently approximate complex functions while requiring fewer layers than MLPs. Motivated by this potential, this paper explores the use of KANs combined with adversarial training and contrastive learning to model the intricate relationship between hazy and clear images. Adversarial training is employed due to its capacity in producing high-fidelity images, and contrastive learning promotes the model’s emphasis on significant features while suppressing the influence of irrelevant information. The proposed UID-KAT framework is trained in an unsupervised setting to take advantage of the abundance of real-world data and address the challenge of preparing paired hazy/clean images. Experimental results show that UID-KAT achieves state-of-the-art dehazing performance across multiple datasets and scenarios, outperforming existing unpaired methods while reducing model complexity. The source code for this work is publicly available at https://github.com/tranleanh/uid-kat.

Medical Image Classification with KAN-Integrated Transformers and Dilated Neighborhood Attention

Authors: Omid Nejati Manzari, Hojat Asgariandehkordi, Taha Koleilat, Yiming Xiao, Hassan Rivaz

Citation Count: 2

Abstract: Convolutional networks, transformers, hybrid models, and Mamba-based architectures have demonstrated strong performance across various medical image classification tasks. However, these methods were primarily designed to classify clean images using labeled data. In contrast, real-world clinical data often involve image corruptions that are unique to multi-center studies and stem from variations in imaging equipment across manufacturers. In this paper, we introduce the Medical Vision Transformer (MedViTV2), a novel architecture incorporating Kolmogorov-Arnold Network (KAN) layers into the transformer architecture for the first time, aiming for generalized medical image classification. We have developed an efficient KAN block to reduce computational load while enhancing the accuracy of the original MedViT. Additionally, to counteract the fragility of our MedViT when scaled up, we propose an enhanced Dilated Neighborhood Attention (DiNA), an adaptation of the efficient fused dot-product attention kernel capable of capturing global context and expanding receptive fields to scale the model effectively and addressing feature collapse issues. Moreover, a hierarchical hybrid strategy is introduced to stack our Local Feature Perception and Global Feature Perception blocks in an efficient manner, which balances local and global feature perceptions to boost performance. Extensive experiments on 17 medical image classification datasets and 12 corrupted medical image datasets demonstrate that MedViTV2 achieved state-of-the-art results in 27 out of 29 experiments with reduced computational complexity. MedViTV2 is 44\% more computationally efficient than the previous version and significantly enhances accuracy, achieving improvements of 4.6\% on MedMNIST, 5.8\% on NonMNIST, and 13.4\% on the MedMNIST-C benchmark.

seqKAN: Sequence processing with Kolmogorov-Arnold Networks

Authors: Tatiana Boura, Stasinos Konstantopoulos

Abstract: Kolmogorov-Arnold Networks (KANs) have been recently proposed as a machine learning framework that is more interpretable and controllable than the multi-layer perceptron. Various network architectures have been proposed within the KAN framework targeting different tasks and application domains, including sequence processing. This paper proposes seqKAN, a new KAN architecture for sequence processing. Although multiple sequence processing KAN architectures have already been proposed, we argue that seqKAN is more faithful to the core concept of the KAN framework. Furthermore, we empirically demonstrate that it achieves better results. The empirical evaluation is performed on generated data from a complex physics problem on an interpolation and an extrapolation task. Using this dataset we compared seqKAN against a prior KAN network for timeseries prediction, recurrent deep networks, and symbolic regression. seqKAN substantially outperforms all architectures, particularly on the extrapolation dataset, while also being the most transparent.

Advancing Out-of-Distribution Detection via Local Neuroplasticity

Authors: Alessandro Canevaro, Julian Schmidt, Mohammad Sajad Marvi, Hang Yu, Georg Martius, Julian Jordan

Venue: International Conference on Learning Representations

Abstract: In the domain of machine learning, the assumption that training and test data share the same distribution is often violated in real-world scenarios, requiring effective out-of-distribution (OOD) detection. This paper presents a novel OOD detection method that leverages the unique local neuroplasticity property of Kolmogorov-Arnold Networks (KANs). Unlike traditional multilayer perceptrons, KANs exhibit local plasticity, allowing them to preserve learned information while adapting to new tasks. Our method compares the activation patterns of a trained KAN against its untrained counterpart to detect OOD samples. We validate our approach on benchmarks from image and medical domains, demonstrating superior performance and robustness compared to state-of-the-art techniques. These results underscore the potential of KANs in enhancing the reliability of machine learning systems in diverse environments.

InSlicing: Interpretable Learning-Assisted Network Slice Configuration in Open Radio Access Networks

Authors: Ming Zhao, Yuru Zhang, Qiang Liu, Ahan Kak, Nakjung Choi

Abstract: Network slicing is a key technology enabling the flexibility and efficiency of 5G networks, offering customized services for diverse applications. However, existing methods face challenges in adapting to dynamic network environments and lack interpretability in performance models. In this paper, we propose a novel interpretable network slice configuration algorithm (\emph{InSlicing}) in open radio access networks, by integrating Kolmogorov-Arnold Networks (KANs) and hybrid optimization process. On the one hand, we use KANs to approximate and learn the unknown performance function of individual slices, which converts the blackbox optimization problem. On the other hand, we solve the converted problem with a genetic method for global search and incorporate a trust region for gradient-based local refinement. With the extensive evaluation, we show that our proposed algorithm achieves high interpretability while reducing 25+\% operation cost than existing solutions.

M4SC: An MLLM-based Multi-modal, Multi-task and Multi-user Semantic Communication System

Authors: Feibo Jiang, Siwei Tu, Li Dong, Kezhi Wang, Kun Yang, Cunhua Pan

Citation Count: 3

Abstract: Multi-modal Large Language Models (MLLMs) are capable of precisely extracting high-level semantic information from multi-modal data, enabling multi-task understanding and generation. This capability facilitates more efficient and intelligent data transmission in semantic communications. In this paper, we design a tailored MLLM for semantic communication and propose an MLLM-based Multi-modal, Multi-task and Multi-user Semantic Communication (M4SC) system. First, we utilize the Kolmogorov-Arnold Network (KAN) to achieve multi-modal alignment in MLLMs, thereby enhancing the accuracy of semantics representation in the semantic space across different modalities. Next, we introduce a multi-task fine-tuning approach based on task instruction following, which leverages a unified task instruction template to describe various semantic communication tasks, improving the MLLM’s ability to follow instructions across multiple tasks. Additionally, by designing a semantic sharing mechanism, we transmit the public and private semantic information of multiple users separately, thus increasing the efficiency of semantic communication. Finally, we employ a joint KAN-LLM-channel coding strategy to comprehensively enhance the performance of the semantic communication system in complex communication environments. Experimental results validate the effectiveness and robustness of the proposed M4SC in multi-modal, multi-task, and multi-user scenarios.

Geometric Kolmogorov-Arnold Superposition Theorem

Authors: Francesco Alesiani, Takashi Maruyama, Henrik Christiansen, Viktor Zaverkin

Abstract: The Kolmogorov-Arnold Theorem (KAT), or more generally, the Kolmogorov Superposition Theorem (KST), establishes that any non-linear multivariate function can be exactly represented as a finite superposition of non-linear univariate functions. Unlike the universal approximation theorem, which provides only an approximate representation without guaranteeing a fixed network size, KST offers a theoretically exact decomposition. The Kolmogorov-Arnold Network (KAN) was introduced as a trainable model to implement KAT, and recent advancements have adapted KAN using concepts from modern neural networks. However, KAN struggles to effectively model physical systems that require inherent equivariance or invariance geometric symmetries as $E(3)$ transformations, a key property for many scientific and engineering applications. In this work, we propose a novel extension of KAT and KAN to incorporate equivariance and invariance over various group actions, including $O(n)$, $O(1,n)$, $S_n$, and general $GL$, enabling accurate and efficient modeling of these systems. Our approach provides a unified approach that bridges the gap between mathematical theory and practical architectures for physical systems, expanding the applicability of KAN to a broader class of problems. We provide experimental validation on molecular dynamical systems and particle physics.

DiffKAN-Inpainting: KAN-based Diffusion model for brain tumor inpainting

Authors: Tianli Tao, Ziyang Wang, Han Zhang, Theodoros N. Arvanitis, Le Zhang

Venue: IEEE International Symposium on Biomedical Imaging

Abstract: Brain tumors delay the standard preprocessing workflow for further examination. Brain inpainting offers a viable, although difficult, solution for tumor tissue processing, which is necessary to improve the precision of the diagnosis and treatment. Most conventional U-Net-based generative models, however, often face challenges in capturing the complex, nonlinear latent representations inherent in brain imaging. In order to accomplish high-quality healthy brain tissue reconstruction, this work proposes DiffKAN-Inpainting, an innovative method that blends diffusion models with the Kolmogorov-Arnold Networks architecture. During the denoising process, we introduce the RePaint method and tumor information to generate images with a higher fidelity and smoother margin. Both qualitative and quantitative results demonstrate that as compared to the state-of-the-art methods, our proposed DiffKAN-Inpainting inpaints more detailed and realistic reconstructions on the BraTS dataset. The knowledge gained from ablation study provide insights for future research to balance performance with computing cost.

LeanKAN: A Parameter-Lean Kolmogorov-Arnold Network Layer with Improved Memory Efficiency and Convergence Behavior

Authors: Benjamin C. Koenig, Suyong Kim, Sili Deng

Citation Count: 2

Abstract: The recently proposed Kolmogorov-Arnold network (KAN) is a promising alternative to multi-layer perceptrons (MLPs) for data-driven modeling. While original KAN layers were only capable of representing the addition operator, the recently-proposed MultKAN layer combines addition and multiplication subnodes in an effort to improve representation performance. Here, we find that MultKAN layers suffer from a few key drawbacks including limited applicability in output layers, bulky parameterizations with extraneous activations, and the inclusion of complex hyperparameters. To address these issues, we propose LeanKANs, a direct and modular replacement for MultKAN and traditional AddKAN layers. LeanKANs address these three drawbacks of MultKAN through general applicability as output layers, significantly reduced parameter counts for a given network structure, and a smaller set of hyperparameters. As a one-to-one layer replacement for standard AddKAN and MultKAN layers, LeanKAN is able to provide these benefits to traditional KAN learning problems as well as augmented KAN structures in which it serves as the backbone, such as KAN Ordinary Differential Equations (KAN-ODEs) or Deep Operator KANs (DeepOKAN). We demonstrate LeanKAN’s simplicity and efficiency in a series of demonstrations carried out across a standard KAN toy problem as well as ordinary and partial differential equations learned via KAN-ODEs, where we find that its sparser parameterization and compact structure serve to increase its expressivity and learning capability, leading it to outperform similar and even much larger MultKANs in various tasks.

Recurrent Neural Networks for Dynamic VWAP Execution: Adaptive Trading Strategies with Temporal Kolmogorov-Arnold Networks

Author: Remi Genet

Citation Count: 1

Abstract: The execution of Volume Weighted Average Price (VWAP) orders remains a critical challenge in modern financial markets, particularly as trading volumes and market complexity continue to increase. In my previous work arXiv:2502.13722, I introduced a novel deep learning approach that demonstrated significant improvements over traditional VWAP execution methods by directly optimizing the execution problem rather than relying on volume curve predictions. However, that model was static because it employed the fully linear approach described in arXiv:2410.21448, which is not designed for dynamic adjustment. This paper extends that foundation by developing a dynamic neural VWAP framework that adapts to evolving market conditions in real time. We introduce two key innovations: first, the integration of recurrent neural networks to capture complex temporal dependencies in market dynamics, and second, a sophisticated dynamic adjustment mechanism that continuously optimizes execution decisions based on market feedback. The empirical analysis, conducted across five major cryptocurrency markets, demonstrates that this dynamic approach achieves substantial improvements over both traditional methods and our previous static implementation, with execution performance gains of 10 to 15% in liquid markets and consistent outperformance across varying conditions. These results suggest that adaptive neural architectures can effectively address the challenges of modern VWAP execution while maintaining computational efficiency suitable for practical deployment.

TSKANMixer: Kolmogorov-Arnold Networks with MLP-Mixer Model for Time Series Forecasting

Authors: Young-Chae Hong, Bei Xiao, Yangho Chen

Citation Count: 2

Abstract: Time series forecasting has long been a focus of research across diverse fields, including economics, energy, healthcare, and traffic management. Recent works have introduced innovative architectures for time series models, such as the Time-Series Mixer (TSMixer), which leverages multi-layer perceptrons (MLPs) to enhance prediction accuracy by effectively capturing both spatial and temporal dependencies within the data. In this paper, we investigate the capabilities of the Kolmogorov-Arnold Networks (KANs) for time-series forecasting by modifying TSMixer with a KAN layer (TSKANMixer). Experimental results demonstrate that TSKANMixer tends to improve prediction accuracy over the original TSMixer across multiple datasets, ranking among the top-performing models compared to other time series approaches. Our results show that the KANs are promising alternatives to improve the performance of time series forecasting by replacing or extending traditional MLPs.

MedKAN: An Advanced Kolmogorov-Arnold Network for Medical Image Classification

Authors: Zhuoqin Yang, Jiansong Zhang, Xiaoling Luo, Zheng Lu, Linlin Shen

Citation Count: 3

Abstract: Recent advancements in deep learning for image classification predominantly rely on convolutional neural networks (CNNs) or Transformer-based architectures. However, these models face notable challenges in medical imaging, particularly in capturing intricate texture details and contextual features. Kolmogorov-Arnold Networks (KANs) represent a novel class of architectures that enhance nonlinear transformation modeling, offering improved representation of complex features. In this work, we present MedKAN, a medical image classification framework built upon KAN and its convolutional extensions. MedKAN features two core modules: the Local Information KAN (LIK) module for fine-grained feature extraction and the Global Information KAN (GIK) module for global context integration. By combining these modules, MedKAN achieves robust feature modeling and fusion. To address diverse computational needs, we introduce three scalable variants–MedKAN-S, MedKAN-B, and MedKAN-L. Experimental results on nine public medical imaging datasets demonstrate that MedKAN achieves superior performance compared to CNN- and Transformer-based models, highlighting its effectiveness and generalizability in medical image analysis.

KAN-powered large-target detection for automotive radar

Authors: Vinay Kulkarni, V. V. Reddy, Neha Maheshwari

Abstract: This paper presents a novel radar signal detection pipeline focused on detecting large targets such as cars and SUVs. Traditional methods, such as Ordered-Statistic Constant False Alarm Rate (OS-CFAR), commonly used in automotive radar, are designed for point or isotropic target models. These may not adequately capture the Range-Doppler (RD) scattering patterns of larger targets, especially in high-resolution radar systems. Additional modules such as association and tracking are necessary to refine and consolidate the detections over multiple dwells. To address these limitations, we propose a detection technique based on the probability density function (pdf) of RD segments, leveraging the Kolmogorov-Arnold neural network (KAN) to learn the data and generate interpretable symbolic expressions for binary hypotheses. Beside the Monte-Carlo study showing better performance for the proposed KAN expression over OS-CFAR, it is shown to exhibit a probability of detection (PD) of 96% when transfer learned with field data. The false alarm rate (PFA) is comparable with OS-CFAR designed with PFA = $10^{-6}$. Additionally, the study also examines impact of the number of pdf bins representing RD segment on performance of the KAN-based detection.

Finding Local Diffusion Schrödinger Bridge using Kolmogorov-Arnold Network

Authors: Xingyu Qiu, Mengying Yang, Xinghua Ma, Fanding Li, Dong Liang, Gongning Luo, Wei Wang, Kuanquan Wang, Shuo Li

Citation Count: 2

Abstract: In image generation, Schrödinger Bridge (SB)-based methods theoretically enhance the efficiency and quality compared to the diffusion models by finding the least costly path between two distributions. However, they are computationally expensive and time-consuming when applied to complex image data. The reason is that they focus on fitting globally optimal paths in high-dimensional spaces, directly generating images as next step on the path using complex networks through self-supervised training, which typically results in a gap with the global optimum. Meanwhile, most diffusion models are in the same path subspace generated by weights $f_A(t)$ and $f_B(t)$, as they follow the paradigm ($x_t = f_A(t)x_{Img} + f_B(t)ε$). To address the limitations of SB-based methods, this paper proposes for the first time to find local Diffusion Schrödinger Bridges (LDSB) in the diffusion path subspace, which strengthens the connection between the SB problem and diffusion models. Specifically, our method optimizes the diffusion paths using Kolmogorov-Arnold Network (KAN), which has the advantage of resistance to forgetting and continuous output. The experiment shows that our LDSB significantly improves the quality and efficiency of image generation using the same pre-trained denoising network and the KAN for optimising is only less than 0.1MB. The FID metric is reduced by more than 15\%, especially with a reduction of 48.50\% when NFE of DDIM is $5$ for the CelebA dataset. Code is available at https://github.com/PerceptionComputingLab/LDSB.

Fast and Accurate Gigapixel Pathological Image Classification with Hierarchical Distillation Multi-Instance Learning

Authors: Jiuyang Dong, Junjun Jiang, Kui Jiang, Jiahan Li, Yongbing Zhang

Abstract: Although multi-instance learning (MIL) has succeeded in pathological image classification, it faces the challenge of high inference costs due to processing numerous patches from gigapixel whole slide images (WSIs). To address this, we propose HDMIL, a hierarchical distillation multi-instance learning framework that achieves fast and accurate classification by eliminating irrelevant patches. HDMIL consists of two key components: the dynamic multi-instance network (DMIN) and the lightweight instance pre-screening network (LIPN). DMIN operates on high-resolution WSIs, while LIPN operates on the corresponding low-resolution counterparts. During training, DMIN are trained for WSI classification while generating attention-score-based masks that indicate irrelevant patches. These masks then guide the training of LIPN to predict the relevance of each low-resolution patch. During testing, LIPN first determines the useful regions within low-resolution WSIs, which indirectly enables us to eliminate irrelevant regions in high-resolution WSIs, thereby reducing inference time without causing performance degradation. In addition, we further design the first Chebyshev-polynomials-based Kolmogorov-Arnold classifier in computational pathology, which enhances the performance of HDMIL through learnable activation layers. Extensive experiments on three public datasets demonstrate that HDMIL outperforms previous state-of-the-art methods, e.g., achieving improvements of 3.13% in AUC while reducing inference time by 28.6% on the Camelyon16 dataset.

March

Fed-KAN: Federated Learning with Kolmogorov-Arnold Networks for Traffic Prediction

Authors: Engin Zeydan, Cristian J. Vaca-Rubio, Luis Blanco, Roberto Pereira, Marius Caus, Kapal Dev

Abstract: Non-Terrestrial Networks (NTNs) are becoming a critical component of modern communication infrastructures, especially with the advent of Low Earth Orbit (LEO) satellite systems. Traditional centralized learning approaches face major challenges in such networks due to high latency, intermittent connectivity and limited bandwidth. Federated Learning (FL) is a promising alternative as it enables decentralized training while maintaining data privacy. However, existing FL models, such as Federated Learning with Multi-Layer Perceptrons (Fed-MLP), can struggle with high computational complexity and poor adaptability to dynamic NTN environments. This paper provides a detailed analysis for Federated Learning with Kolmogorov-Arnold Networks (Fed-KAN), its implementation and performance improvements over traditional FL models in NTN environments for traffic forecasting. The proposed Fed-KAN is a novel approach that utilises the functional approximation capabilities of KANs in a FL framework. We evaluate Fed-KAN compared to Fed-MLP on a traffic dataset of real satellite operator and show a significant reduction in training and test loss. Our results show that Fed-KAN can achieve a 77.39% reduction in average test loss compared to Fed-MLP, highlighting its improved performance and better generalization ability. At the end of the paper, we also discuss some potential applications of Fed-KAN within O-RAN and Fed-KAN usage for split functionalities in NTN architecture.

ViKANformer: Embedding Kolmogorov Arnold Networks in Vision Transformers for Pattern-Based Learning

Authors: Shreyas S, Akshath M

Abstract: Vision Transformers (ViTs) have significantly advanced image classification by applying self-attention on patch embeddings. However, the standard MLP blocks in each Transformer layer may not capture complex nonlinear dependencies optimally. In this paper, we propose ViKANformer, a Vision Transformer where we replace the MLP sub-layers with Kolmogorov-Arnold Network (KAN) expansions, including Vanilla KAN, Efficient-KAN, Fast-KAN, SineKAN, and FourierKAN, while also examining a Flash Attention variant. By leveraging the Kolmogorov-Arnold theorem, which guarantees that multivariate continuous functions can be expressed via sums of univariate continuous functions, we aim to boost representational power. Experimental results on MNIST demonstrate that SineKAN, Fast-KAN, and a well-tuned Vanilla KAN can achieve over 97% accuracy, albeit with increased training overhead. This trade-off highlights that KAN expansions may be beneficial if computational cost is acceptable. We detail the expansions, present training/test accuracy and F1/ROC metrics, and provide pseudocode and hyperparameters for reproducibility. Finally, we compare ViKANformer to a simple MLP and a small CNN baseline on MNIST, illustrating the efficiency of Transformer-based methods even on a small-scale dataset.

PostHoc FREE Calibrating on Kolmogorov Arnold Networks

Authors: Wenhao Liang, Wei Emma Zhang, Lin Yue, Miao Xu, Olaf Maennel, Weitong Chen

Abstract: Kolmogorov Arnold Networks (KANs) are neural architectures inspired by the Kolmogorov Arnold representation theorem that leverage B Spline parameterizations for flexible, locally adaptive function approximation. Although KANs can capture complex nonlinearities beyond those modeled by standard MultiLayer Perceptrons (MLPs), they frequently exhibit miscalibrated confidence estimates manifesting as overconfidence in dense data regions and underconfidence in sparse areas. In this work, we systematically examine the impact of four critical hyperparameters including Layer Width, Grid Order, Shortcut Function, and Grid Range on the calibration of KANs. Furthermore, we introduce a novel TemperatureScaled Loss (TSL) that integrates a temperature parameter directly into the training objective, dynamically adjusting the predictive distribution during learning. Both theoretical analysis and extensive empirical evaluations on standard benchmarks demonstrate that TSL significantly reduces calibration errors, thereby improving the reliability of probabilistic predictions. Overall, our study provides actionable insights into the design of spline based neural networks and establishes TSL as a robust loss solution for enhancing calibration.

Energy-Dissipative Evolutionary Kolmogorov-Arnold Networks for Complex PDE Systems

Authors: Guang Lin, Changhong Mou, Jiahao Zhang

Citation Count: 1

Abstract: We introduce evolutionary Kolmogorov-Arnold Networks (EvoKAN), a novel framework for solving complex partial differential equations (PDEs). EvoKAN builds on Kolmogorov-Arnold Networks (KANs), where activation functions are spline based and trainable on each edge, offering localized flexibility across multiple scales. Rather than retraining the network repeatedly, EvoKAN encodes only the PDE’s initial state during an initial learning phase. The network parameters then evolve numerically, governed by the same PDE, without any additional optimization. By treating these parameters as continuous functions in the relevant coordinates and updating them through time steps, EvoKAN can predict system trajectories over arbitrarily long horizons, a notable challenge for many conventional neural-network based methods. In addition, EvoKAN integrates the scalar auxiliary variable (SAV) method to guarantee unconditional energy stability and computational efficiency. At individual time step, SAV only needs to solve decoupled linear systems with constant coefficients, the implementation is significantly simplified. We test the proposed framework in several complex PDEs, including one dimensional and two dimensional Allen-Cahn equations and two dimensional Navier-Stokes equations. Numerical results show that EvoKAN solutions closely match analytical references and established numerical benchmarks, effectively capturing both phase-field phenomena (Allen-Cahn) and turbulent flows (Navier-Stokes).

Relating Piecewise Linear Kolmogorov Arnold Networks to ReLU Networks

Authors: Nandi Schoots, Mattia Jacopo Villani, Niels uit de Bos

Abstract: Kolmogorov-Arnold Networks are a new family of neural network architectures which holds promise for overcoming the curse of dimensionality and has interpretability benefits (arXiv:2404.19756). In this paper, we explore the connection between Kolmogorov Arnold Networks (KANs) with piecewise linear (univariate real) functions and ReLU networks. We provide completely explicit constructions to convert a piecewise linear KAN into a ReLU network and vice versa.

A Kolmogorov-Arnold Network for Explainable Detection of Cyberattacks on EV Chargers

Authors: Ahmad Mohammad Saber, Max Mauro Dias Santos, Mohammad Al Janaideh, Amr Youssef, Deepa Kundur

Abstract: The increasing adoption of Electric Vehicles (EVs) and the expansion of charging infrastructure and their reliance on communication expose Electric Vehicle Supply Equipment (EVSE) to cyberattacks. This paper presents a novel Kolmogorov-Arnold Network (KAN)-based framework for detecting cyberattacks on EV chargers using only power consumption measurements. Leveraging the KAN’s capability to model nonlinear, high-dimensional functions and its inherently interpretable architecture, the framework effectively differentiates between normal and malicious charging scenarios. The model is trained offline on a comprehensive dataset containing over 100,000 cyberattack cases generated through an experimental setup. Once trained, the KAN model can be deployed within individual chargers for real-time detection of abnormal charging behaviors indicative of cyberattacks. Our results demonstrate that the proposed KAN-based approach can accurately detect cyberattacks on EV chargers with Precision and F1-score of 99% and 92%, respectively, outperforming existing detection methods. Additionally, the proposed KANs’s enable the extraction of mathematical formulas representing KAN’s detection decisions, addressing interpretability, a key challenge in deep learning-based cybersecurity frameworks. This work marks a significant step toward building secure and explainable EV charging infrastructure.

As Good as It KAN Get: High-Fidelity Audio Representation

Authors: Patryk Marszałek, Maciej Rut, Piotr Kawa, Przemysław Spurek, Piotr Syga

Abstract: Implicit neural representations (INR) have gained prominence for efficiently encoding multimedia data, yet their applications in audio signals remain limited. This study introduces the Kolmogorov-Arnold Network (KAN), a novel architecture using learnable activation functions, as an effective INR model for audio representation. KAN demonstrates superior perceptual performance over previous INRs, achieving the lowest Log-SpectralDistance of 1.29 and the highest Perceptual Evaluation of Speech Quality of 3.57 for 1.5 s audio. To extend KAN’s utility, we propose FewSound, a hypernetwork-based architecture that enhances INR parameter updates. FewSound outperforms the state-of-the-art HyperSound, with a 33.3% improvement in MSE and 60.87% in SI-SNR. These results show KAN as a robust and adaptable audio representation with the potential for scalability and integration into various hypernetwork frameworks. The source code can be accessed at https://github.com/gmum/fewsound.git.

Deterministic Global Optimization over trained Kolmogorov Arnold Networks

Authors: Tanuj Karia, Giacomo Lastrucci, Artur M. Schweidtmann

Abstract: To address the challenge of tractability for optimizing mathematical models in science and engineering, surrogate models are often employed. Recently, a new class of machine learning models named Kolmogorov Arnold Networks (KANs) have been proposed. It was reported that KANs can approximate a given input/output relationship with a high level of accuracy, requiring significantly fewer parameters than multilayer perceptrons. Hence, we aim to assess the suitability of deterministic global optimization of trained KANs by proposing their Mixed-Integer Nonlinear Programming (MINLP) formulation. We conduct extensive computational experiments for different KAN architectures. Additionally, we propose alternative convex hull reformulation, local support and redundant constraints for the formulation aimed at improving the effectiveness of the MINLP formulation of the KAN. KANs demonstrate high accuracy while requiring relatively modest computational effort to optimize them, particularly for cases with less than five inputs or outputs. For cases with higher inputs or outputs, carefully considering the KAN architecture during training may improve its effectiveness while optimizing over a trained KAN. Overall, we observe that KANs offer a promising alternative as surrogate models for deterministic global optimization.

Implicit U-KAN2.0: Dynamic, Efficient and Interpretable Medical Image Segmentation

Authors: Chun-Wun Cheng, Yining Zhao, Yanqi Cheng, Javier A. Montoya-Zegarra, Carola-Bibiane Schönlieb, Angelica I Aviles-Rivero

Abstract: Image segmentation is a fundamental task in both image analysis and medical applications. State-of-the-art methods predominantly rely on encoder-decoder architectures with a U-shaped design, commonly referred to as U-Net. Recent advancements integrating transformers and MLPs improve performance but still face key limitations, such as poor interpretability, difficulty handling intrinsic noise, and constrained expressiveness due to discrete layer structures, often lacking a solid theoretical foundation.In this work, we introduce Implicit U-KAN 2.0, a novel U-Net variant that adopts a two-phase encoder-decoder structure. In the SONO phase, we use a second-order neural ordinary differential equation (NODEs), called the SONO block, for a more efficient, expressive, and theoretically grounded modeling approach. In the SONO-MultiKAN phase, we integrate the second-order NODEs and MultiKAN layer as the core computational block to enhance interpretability and representation power. Our contributions are threefold. First, U-KAN 2.0 is an implicit deep neural network incorporating MultiKAN and second order NODEs, improving interpretability and performance while reducing computational costs. Second, we provide a theoretical analysis demonstrating that the approximation ability of the MultiKAN block is independent of the input dimension. Third, we conduct extensive experiments on a variety of 2D and a single 3D dataset, demonstrating that our model consistently outperforms existing segmentation networks. Project Website: https://math-ml-x.github.io/IUKAN2/

TrafficKAN-GCN: Graph Convolutional-based Kolmogorov-Arnold Network for Traffic Flow Optimization

Authors: Jiayi Zhang, Yiming Zhang, Yuan Zheng, Yuchen Wang, Jinjiang You, Yuchen Xu, Wenxing Jiang, Soumyabrata Dev

Abstract: Urban traffic optimization is critical for improving transportation efficiency and alleviating congestion, particularly in large-scale dynamic networks. Traditional methods, such as Dijkstra’s and Floyd’s algorithms, provide effective solutions in static settings, but they struggle with the spatial-temporal complexity of real-world traffic flows. In this work, we propose TrafficKAN-GCN, a hybrid deep learning framework combining Kolmogorov-Arnold Networks (KAN) with Graph Convolutional Networks (GCN), designed to enhance urban traffic flow optimization. By integrating KAN’s adaptive nonlinear function approximation with GCN’s spatial graph learning capabilities, TrafficKAN-GCN captures both complex traffic patterns and topological dependencies. We evaluate the proposed framework using real-world traffic data from the Baltimore Metropolitan area. Compared with baseline models such as MLP-GCN, standard GCN, and Transformer-based approaches, TrafficKAN-GCN achieves competitive prediction accuracy while demonstrating improved robustness in handling noisy and irregular traffic data. Our experiments further highlight the framework’s ability to redistribute traffic flow, mitigate congestion, and adapt to disruptive events, such as the Francis Scott Key Bridge collapse. This study contributes to the growing body of work on hybrid graph learning for intelligent transportation systems, highlighting the potential of combining KAN and GCN for real-time traffic optimization. Future work will focus on reducing computational overhead and integrating Transformer-based temporal modeling for enhanced long-term traffic prediction. The proposed TrafficKAN-GCN framework offers a promising direction for data-driven urban mobility management, balancing predictive accuracy, robustness, and computational efficiency.

Can KAN CANs? Input-convex Kolmogorov-Arnold Networks (KANs) as hyperelastic constitutive artificial neural networks (CANs)

Authors: Prakash Thakolkaran, Yaqi Guo, Shivam Saini, Mathias Peirlinck, Benjamin Alheit, Siddhant Kumar

Venue: Computer Methods in Applied Mechanics and Engineering

Abstract: Traditional constitutive models rely on hand-crafted parametric forms with limited expressivity and generalizability, while neural network-based models can capture complex material behavior but often lack interpretability. To balance these trade-offs, we present monotonic Input-Convex Kolmogorov-Arnold Networks (ICKANs) for learning polyconvex hyperelastic constitutive laws. ICKANs leverage the Kolmogorov-Arnold representation, decomposing the model into compositions of trainable univariate spline-based activation functions for rich expressivity. We introduce trainable monotonic input-convex splines within the KAN architecture, ensuring physically admissible polyconvex models for isotropic compressible hyperelasticity. The resulting models are both compact and interpretable, enabling explicit extraction of analytical constitutive relationships through a monotonic input-convex symbolic regression technique. Through unsupervised training on full-field strain data and limited global force measurements, ICKANs accurately capture nonlinear stress-strain behavior across diverse strain states. Finite element simulations of unseen geometries with trained ICKAN hyperelastic constitutive models confirm the framework’s robustness and generalization capability.

AF-KAN: Activation Function-Based Kolmogorov-Arnold Networks for Efficient Representation Learning

Authors: Hoang-Thang Ta, Anh Tran

Abstract: Kolmogorov-Arnold Networks (KANs) have inspired numerous works exploring their applications across a wide range of scientific problems, with the potential to replace Multilayer Perceptrons (MLPs). While many KANs are designed using basis and polynomial functions, such as B-splines, ReLU-KAN utilizes a combination of ReLU functions to mimic the structure of B-splines and take advantage of ReLU’s speed. However, ReLU-KAN is not built for multiple inputs, and its limitations stem from ReLU’s handling of negative values, which can restrict feature extraction. To address these issues, we introduce Activation Function-Based Kolmogorov-Arnold Networks (AF-KAN), expanding ReLU-KAN with various activations and their function combinations. This novel KAN also incorporates parameter reduction methods, primarily attention mechanisms and data normalization, to enhance performance on image classification datasets. We explore different activation functions, function combinations, grid sizes, and spline orders to validate the effectiveness of AF-KAN and determine its optimal configuration. In the experiments, AF-KAN significantly outperforms MLP, ReLU-KAN, and other KANs with the same parameter count. It also remains competitive even when using fewer than 6 to 10 times the parameters while maintaining the same network structure. However, AF-KAN requires a longer training time and consumes more FLOPs. The repository for this work is available at https://github.com/hoangthangta/All-KAN.

Exploring Adversarial Transferability between Kolmogorov-arnold Networks

Authors: Songping Wang, Xinquan Yue, Yueming Lyu, Caifeng Shan

Citation Count: 1

Abstract: Kolmogorov-Arnold Networks (KANs) have emerged as a transformative model paradigm, significantly impacting various fields. However, their adversarial robustness remains less underexplored, especially across different KAN architectures. To explore this critical safety issue, we conduct an analysis and find that due to overfitting to the specific basis functions of KANs, they possess poor adversarial transferability among different KANs. To tackle this challenge, we propose AdvKAN, the first transfer attack method for KANs. AdvKAN integrates two key components: 1) a Breakthrough-Defense Surrogate Model (BDSM), which employs a breakthrough-defense training strategy to mitigate overfitting to the specific structures of KANs. 2) a Global-Local Interaction (GLI) technique, which promotes sufficient interaction between adversarial gradients of hierarchical levels, further smoothing out loss surfaces of KANs. Both of them work together to enhance the strength of transfer attack among different KANs. Extensive experimental results on various KANs and datasets demonstrate the effectiveness of AdvKAN, which possesses notably superior attack capabilities and deeply reveals the vulnerabilities of KANs. Code will be released upon acceptance.

NukesFormers: Unpaired Hyperspectral Image Generation with Non-Uniform Domain Alignment

Authors: Jiaojiao Li, Shiyao Duan, Haitao XU, Rui Song

Abstract: The inherent difficulty in acquiring accurately co-registered RGB-hyperspectral image (HSI) pairs has significantly impeded the practical deployment of current data-driven Hyperspectral Image Generation (HIG) networks in engineering applications. Gleichzeitig, the ill-posed nature of the aligning constraints, compounded with the complexities of mining cross-domain features, also hinders the advancement of unpaired HIG (UnHIG) tasks. In this paper, we conquer these challenges by modeling the UnHIG to range space interaction and compensations of null space through Range-Null Space Decomposition (RND) methodology. Specifically, the introduced contrastive learning effectively aligns the geometric and spectral distributions of unpaired data by building the interaction of range space, considering the consistent feature in degradation process. Following this, we map the frequency representations of dual-domain input and thoroughly mining the null space, like degraded and high-frequency components, through the proposed Non-uniform Kolmogorov-Arnold Networks. Extensive comparative experiments demonstrate that it establishes a new benchmark in UnHIG.

KAN-Mixers: a new deep learning architecture for image classification

Authors: Jorge Luiz dos Santos Canuto, Linnyer Beatrys Ruiz Aylon, Rodrigo Clemente Thom de Souza

Abstract: Due to their effective performance, Convolutional Neural Network (CNN) and Vision Transformer (ViT) architectures have become the standard for solving computer vision tasks. Such architectures require large data sets and rely on convolution and self-attention operations. In 2021, MLP-Mixer emerged, an architecture that relies only on Multilayer Perceptron (MLP) and achieves extremely competitive results when compared to CNNs and ViTs. Despite its good performance in computer vision tasks, the MLP-Mixer architecture may not be suitable for refined feature extraction in images. Recently, the Kolmogorov-Arnold Network (KAN) was proposed as a promising alternative to MLP models. KANs promise to improve accuracy and interpretability when compared to MLPs. Therefore, the present work aims to design a new mixer-based architecture, called KAN-Mixers, using KANs as main layers and evaluate its performance, in terms of several performance metrics, in the image classification task. As main results obtained, the KAN-Mixers model was superior to the MLP, MLP-Mixer and KAN models in the Fashion-MNIST and CIFAR-10 datasets, with 0.9030 and 0.6980 of average accuracy, respectively.

Extracting Transport Properties of Quark-Gluon Plasma from the Heavy-Quark Potential With Neural Networks in a Holographic Model

Authors: Wen-Chao Dai, Ou-Yang Luo, Bing Chen, Xun Chen, Xiao-Yan Zhu, Xiao-Hua Li

Abstract: Using Kolmogorov-Arnold Networks (KANs), we construct a holographic model informed by lattice QCD data. This neural network approach enables the derivation of an analytical solution for the deformation factor $w(r)$ and the determination of a constant $g$ related to the string tension. Within the KANs-based holographic framework, we further analyze heavy quark potentials under finite temperature and chemical potential conditions. Additionally, we calculate the drag force, jet quenching parameter, and diffusion coefficient of heavy quarks in this paper. Our findings demonstrate qualitative consistency with both experimental measurements and established phenomenological model.

Kolmogorov-Arnold Attention: Is Learnable Attention Better For Vision Transformers?

Authors: Subhajit Maity, Killian Hitsman, Xin Li, Aritra Dutta

Abstract: Kolmogorov-Arnold networks (KANs) are a remarkable innovation that consists of learnable activation functions, with the potential to capture more complex relationships from data. Presently, KANs are deployed by replacing multilayer perceptrons (MLPs) in deep networks, including advanced architectures such as vision Transformers (ViTs). This work asks whether KAN could learn token interactions. In this paper, we design the first learnable attention called Kolmogorov-Arnold Attention (KArAt) for ViTs that can operate on any basis, ranging from Fourier, Wavelets, Splines, to Rational Functions. However, learnable activations in the attention cause a memory explosion. To remedy this, we propose a modular version of KArAt that uses a low-rank approximation. By adopting the Fourier basis, Fourier-KArAt and its variants, in some cases, outperform their traditional softmax counterparts, or show comparable performance on CIFAR-10, CIFAR-100, and ImageNet-1K. We also deploy Fourier KArAt to ConViT and Swin-Transformer, and use it in detection and segmentation with ViT-Det. We dissect the performance of these architectures by analyzing their loss landscapes, weight distributions, optimizer paths, attention visualizations, and transferability to other datasets. KArAt’s learnable activation yields a better attention score across all ViTs, indicating improved token-to-token interactions and contributing to enhanced inference. Still, its generalizability does not scale with larger ViTs. However, many factors, including the present computing interface, affect the relative performance of parameter- and memory-heavy KArAts. We note that the goal of this paper is not to produce efficient attention or challenge the traditional activations; by designing KArAt, we are the first to show that attention can be learned and encourage researchers to explore KArAt in conjunction with more advanced architectures.

Color Matching Using Hypernetwork-Based Kolmogorov-Arnold Networks

Authors: Artem Nikonorov, Georgy Perevozchikov, Andrei Korepanov, Nancy Mehta, Mahmoud Afifi, Egor Ershov, Radu Timofte

Abstract: We present cmKAN, a versatile framework for color matching. Given an input image with colors from a source color distribution, our method effectively and accurately maps these colors to match a target color distribution in both supervised and unsupervised settings. Our framework leverages the spline capabilities of Kolmogorov-Arnold Networks (KANs) to model the color matching between source and target distributions. Specifically, we developed a hypernetwork that generates spatially varying weight maps to control the nonlinear splines of a KAN, enabling accurate color matching. As part of this work, we introduce a first large-scale dataset of paired images captured by two distinct cameras and evaluate the efficacy of our and existing methods in matching colors. We evaluated our approach across various color-matching tasks, including: (1) raw-to-raw mapping, where the source color distribution is in one camera’s raw color space and the target in another camera’s raw space; (2) raw-to-sRGB mapping, where the source color distribution is in a camera’s raw space and the target is in the display sRGB space, emulating the color rendering of a camera ISP; and (3) sRGB-to-sRGB mapping, where the goal is to transfer colors from a source sRGB space (e.g., produced by a source camera ISP) to a target sRGB space (e.g., from a different camera ISP). The results show that our method outperforms existing approaches by 37.3% on average for supervised and unsupervised cases while remaining lightweight compared to other methods. The codes, dataset, and pre-trained models are available at: https://github.com/gosha20777/cmKAN

HyperKAN: Hypergraph Representation Learning with Kolmogorov-Arnold Networks

Authors: Xiangfei Fang, Boying Wang, Chengying Huan, Shaonan Ma, Heng Zhang, Chen Zhao

Abstract: Hypergraph representation learning has garnered increasing attention across various domains due to its capability to model high-order relationships. Traditional methods often rely on hypergraph neural networks (HNNs) employing message passing mechanisms to aggregate vertex and hyperedge features. However, these methods are constrained by their dependence on hypergraph topology, leading to the challenge of imbalanced information aggregation, where high-degree vertices tend to aggregate redundant features, while low-degree vertices often struggle to capture sufficient structural features. To overcome the above challenges, we introduce HyperKAN, a novel framework for hypergraph representation learning that transcends the limitations of message-passing techniques. HyperKAN begins by encoding features for each vertex and then leverages Kolmogorov-Arnold Networks (KANs) to capture complex nonlinear relationships. By adjusting structural features based on similarity, our approach generates refined vertex representations that effectively addresses the challenge of imbalanced information aggregation. Experiments conducted on the real-world datasets demonstrate that HyperKAN significantly outperforms state of-the-art HNN methods, achieving nearly a 9% performance improvement on the Senate dataset.

From Zero to Detail: Deconstructing Ultra-High-Definition Image Restoration from Progressive Spectral Perspective

Authors: Chen Zhao, Zhizhou Chen, Yunzhe Xu, Enxuan Gu, Jian Li, Zili Yi, Qian Wang, Jian Yang, Ying Tai

Abstract: Ultra-high-definition (UHD) image restoration faces significant challenges due to its high resolution, complex content, and intricate details. To cope with these challenges, we analyze the restoration process in depth through a progressive spectral perspective, and deconstruct the complex UHD restoration problem into three progressive stages: zero-frequency enhancement, low-frequency restoration, and high-frequency refinement. Building on this insight, we propose a novel framework, ERR, which comprises three collaborative sub-networks: the zero-frequency enhancer (ZFE), the low-frequency restorer (LFR), and the high-frequency refiner (HFR). Specifically, the ZFE integrates global priors to learn global mapping, while the LFR restores low-frequency information, emphasizing reconstruction of coarse-grained content. Finally, the HFR employs our designed frequency-windowed kolmogorov-arnold networks (FW-KAN) to refine textures and details, producing high-quality image restoration. Our approach significantly outperforms previous UHD methods across various tasks, with extensive ablation studies validating the effectiveness of each component. The code is available at \href{https://github.com/NJU-PCALab/ERR}{here}.

KANITE: Kolmogorov-Arnold Networks for ITE estimation

Authors: Eshan Mehendale, Abhinav Thorat, Ravi Kolla, Niranjan Pedanekar

Abstract: We introduce KANITE, a framework leveraging Kolmogorov-Arnold Networks (KANs) for Individual Treatment Effect (ITE) estimation under multiple treatments setting in causal inference. By utilizing KAN’s unique abilities to learn univariate activation functions as opposed to learning linear weights by Multi-Layer Perceptrons (MLPs), we improve the estimates of ITEs. The KANITE framework comprises two key architectures: 1.Integral Probability Metric (IPM) architecture: This employs an IPM loss in a specialized manner to effectively align towards ITE estimation across multiple treatments. 2. Entropy Balancing (EB) architecture: This uses weights for samples that are learned by optimizing entropy subject to balancing the covariates across treatment groups. Extensive evaluations on benchmark datasets demonstrate that KANITE outperforms state-of-the-art algorithms in both $ε_{\text{PEHE}}$ and $ε_{\text{ATE}}$ metrics. Our experiments highlight the advantages of KANITE in achieving improved causal estimates, emphasizing the potential of KANs to advance causal inference methodologies across diverse application areas.

Semi-KAN: KAN Provides an Effective Representation for Semi-Supervised Learning in Medical Image Segmentation

Authors: Zanting Ye, Xiaolong Niu, Xuanbin Wu, Wenxiang Yi, Yuan Chang, Lijun Lu

Abstract: Deep learning-based medical image segmentation has shown remarkable success; however, it typically requires extensive pixel-level annotations, which are both expensive and time-intensive. Semi-supervised medical image segmentation (SSMIS) offers a viable alternative, driven by advancements in CNNs and ViTs. However, these networks often rely on single fixed activation functions and linear modeling patterns, limiting their ability to effectively learn robust representations. Given the limited availability of labeled date, achieving robust representation learning becomes crucial. Inspired by Kolmogorov-Arnold Networks (KANs), we propose Semi-KAN, which leverages the untapped potential of KANs to enhance backbone architectures for representation learning in SSMIS. Our findings indicate that: (1) compared to networks with fixed activation functions, KANs exhibit superior representation learning capabilities with fewer parameters, and (2) KANs excel in high-semantic feature spaces. Building on these insights, we integrate KANs into tokenized intermediate representations, applying them selectively at the encoder’s bottleneck and the decoder’s top layers within a U-Net pipeline to extract high-level semantic features. Although learnable activation functions improve feature expansion, they introduce significant computational overhead with only marginal performance gains. To mitigate this, we reduce the feature dimensions and employ horizontal scaling to capture multiple pattern representations. Furthermore, we design a multi-branch U-Net architecture with uncertainty estimation to effectively learn diverse pattern representations. Extensive experiments on four public datasets demonstrate that Semi-KAN surpasses baseline networks, utilizing fewer KAN layers and lower computational cost, thereby underscoring the potential of KANs as a promising approach for SSMIS.

Kolmogorov-Arnold Network for Transistor Compact Modeling

Authors: Rodion Novkin, Hussam Amrouch

Abstract: Neural network (NN)-based transistor compact modeling has recently emerged as a transformative solution for accelerating device modeling and SPICE circuit simulations. However, conventional NN architectures, despite their widespread adoption in state-of-the-art methods, primarily function as black-box problem solvers. This lack of interpretability significantly limits their capacity to extract and convey meaningful insights into learned data patterns, posing a major barrier to their broader adoption in critical modeling tasks. This work introduces, for the first time, Kolmogorov-Arnold network (KAN) for the transistor - a groundbreaking NN architecture that seamlessly integrates interpretability with high precision in physics-based function modeling. We systematically evaluate the performance of KAN and Fourier KAN for FinFET compact modeling, benchmarking them against the golden industry-standard compact model and the widely used MLP architecture. Our results reveal that KAN and FKAN consistently achieve superior prediction accuracy for critical figures of merit, including gate current, drain charge, and source charge. Furthermore, we demonstrate and improve the unique ability of KAN to derive symbolic formulas from learned data patterns - a capability that not only enhances interpretability but also facilitates in-depth transistor analysis and optimization. This work highlights the transformative potential of KAN in bridging the gap between interpretability and precision in NN-driven transistor compact modeling. By providing a robust and transparent approach to transistor modeling, KAN represents a pivotal advancement for the semiconductor industry as it navigates the challenges of advanced technology scaling.

Identifying Ising and percolation phase transitions based on KAN method

Authors: Dian Xu, Shanshan Wang, Wei Li, Weibing Deng, Feng Gao, Jianmin Shen

Abstract: Modern machine learning, grounded in the Universal Approximation Theorem, has achieved significant success in the study of phase transitions in both equilibrium and non-equilibrium systems. However, identifying the critical points of percolation models using raw configurations remains a challenging and intriguing problem. This paper proposes the use of the Kolmogorov-Arnold Network, which is based on the Kolmogorov-Arnold Representation Theorem, to input raw configurations into a learning model. The results demonstrate that the KAN can indeed predict the critical points of percolation models. Further observation reveals that, apart from models associated with the density of occupied points, KAN is also capable of effectively achieving phase classification for models where the sole alteration pertains to the orientation of spins, resulting in an order parameter that manifests as an external magnetic flux, such as the Ising model.

Surrogate Learning in Meta-Black-Box Optimization: A Preliminary Study

Authors: Zeyuan Ma, Zhiyang Huang, Jiacheng Chen, Zhiguang Cao, Yue-Jiao Gong

Citation Count: 3

Abstract: Recent Meta-Black-Box Optimization (MetaBBO) approaches have shown possibility of enhancing the optimization performance through learning meta-level policies to dynamically configure low-level optimizers. However, existing MetaBBO approaches potentially consume massive function evaluations to train their meta-level policies. Inspired by the recent trend of using surrogate models for cost-friendly evaluation of expensive optimization problems, in this paper, we propose a novel MetaBBO framework which combines surrogate learning process and reinforcement learning-aided Differential Evolution algorithm, namely Surr-RLDE, to address the intensive function evaluation in MetaBBO. Surr-RLDE comprises two learning stages: surrogate learning and policy learning. In surrogate learning, we train a Kolmogorov-Arnold Networks (KAN) with a novel relative-order-aware loss to accurately approximate the objective functions of the problem instances used for subsequent policy learning. In policy learning, we employ reinforcement learning (RL) to dynamically configure the mutation operator in DE. The learned surrogate model is integrated into the training of the RL-based policy to substitute for the original objective function, which effectively reduces consumed evaluations during policy learning. Extensive benchmark results demonstrate that Surr-RLDE not only shows competitive performance to recent baselines, but also shows compelling generalization for higher-dimensional problems. Further ablation studies underscore the effectiveness of each technical components in Surr-RLDE. We open-source Surr-RLDE at https://github.com/GMC-DRL/Surr-RLDE.

Prompt-Guided Dual-Path UNet with Mamba for Medical Image Segmentation

Authors: Shaolei Zhang, Jinyan Liu, Tianyi Qian, Xuesong Li

Abstract: Convolutional neural networks (CNNs) and transformers are widely employed in constructing UNet architectures for medical image segmentation tasks. However, CNNs struggle to model long-range dependencies, while transformers suffer from quadratic computational complexity. Recently, Mamba, a type of State Space Models, has gained attention for its exceptional ability to model long-range interactions while maintaining linear computational complexity. Despite the emergence of several Mamba-based methods, they still present the following limitations: first, their network designs generally lack perceptual capabilities for the original input data; second, they primarily focus on capturing global information, while often neglecting local details. To address these challenges, we propose a prompt-guided CNN-Mamba dual-path UNet, termed PGM-UNet, for medical image segmentation. Specifically, we introduce a prompt-guided residual Mamba module that adaptively extracts dynamic visual prompts from the original input data, effectively guiding Mamba in capturing global information. Additionally, we design a local-global information fusion network, comprising a local information extraction module, a prompt-guided residual Mamba module, and a multi-focus attention fusion module, which effectively integrates local and global information. Furthermore, inspired by Kolmogorov-Arnold Networks (KANs), we develop a multi-scale information extraction module to capture richer contextual information without altering the resolution. We conduct extensive experiments on the ISIC-2017, ISIC-2018, DIAS, and DRIVE. The results demonstrate that the proposed method significantly outperforms state-of-the-art approaches in multiple medical image segmentation tasks.

KAC: Kolmogorov-Arnold Classifier for Continual Learning

Authors: Yusong Hu, Zichen Liang, Fei Yang, Qibin Hou, Xialei Liu, Ming-Ming Cheng

Citation Count: 1

Abstract: Continual learning requires models to train continuously across consecutive tasks without forgetting. Most existing methods utilize linear classifiers, which struggle to maintain a stable classification space while learning new tasks. Inspired by the success of Kolmogorov-Arnold Networks (KAN) in preserving learning stability during simple continual regression tasks, we set out to explore their potential in more complex continual learning scenarios. In this paper, we introduce the Kolmogorov-Arnold Classifier (KAC), a novel classifier developed for continual learning based on the KAN structure. We delve into the impact of KAN’s spline functions and introduce Radial Basis Functions (RBF) for improved compatibility with continual learning. We replace linear classifiers with KAC in several recent approaches and conduct experiments across various continual learning benchmarks, all of which demonstrate performance improvements, highlighting the effectiveness and robustness of KAC in continual learning. The code is available at https://github.com/Ethanhuhuhu/KAC.

Adaptive Variational Quantum Kolmogorov-Arnold Network

Authors: Hikaru Wakaura, Rahmat Mulyawan, Andriyan B. Suksmono

Citation Count: 1

Abstract: Kolmogorov-Arnold Network (KAN) is a novel multi-layer neuromorphic network. Many groups worldwide have studied this network, including image processing, time series analysis, solving physical problems, and practical applications such as medical use. Therefore, we propose an Adaptive Variational Quantum Kolmogorov-Arnold Network (VQKAN) that takes advantage of KAN for Variational Quantum Algorithms in an adaptive manner. The Adaptive VQKAN is VQKAN that uses adaptive ansatz as the ansatz and repeat VQKAN growing the ansatz just like Adaptive Variational Quantum Eigensolver (VQE). The scheme inspired by Adaptive VQE is promised to ascend the accuracy of VQKAN to practical value. As a result, Adaptive VQKAN has been revealed to calculate the fitting problem more accurately and faster than Quantum Neural Networks by far less number of parametric gates.

Enhanced Variational Quantum Kolmogorov-Arnold Network

Authors: Hikaru Wakaura, Rahmat Mulyawan, Andriyan B. Suksmono

Abstract: The Kolmogorov-Arnold Network (KAN) is a novel multi-layer network model recognized for its efficiency in neuromorphic computing, where synapses between neurons are trained linearly. Computations in KAN are performed by generating a polynomial vector from the state vector and layer-wise trained synapses, enabling efficient processing. While KAN can be implemented on quantum computers using block encoding and Quantum Signal Processing, these methods require fault-tolerant quantum devices, making them impractical for current Noisy Intermediate-Scale Quantum (NISQ) hardware. We propose the Enhanced Variational Quantum Kolmogorov-Arnold Network (EVQKAN) to overcome this limitation, which emulates KAN through variational quantum algorithms. The EVQKAN ansatz employs a tiling technique to emulate layer matrices, leading to significantly higher accuracy compared to conventional Variational Quantum Kolmogorov-Arnold Network (VQKAN) and Quantum Neural Networks (QNN), even with a smaller number of layers. EVQKAN achieves superior performance with a single-layer architecture, whereas QNN and VQKAN typically struggle. Additionally, EVQKAN eliminates the need for Quantum Signal Processing, enhancing its robustness to noise and making it well-suited for practical deployment on NISQ-era quantum devices.

Interpretable Graph Kolmogorov-Arnold Networks for Multi-Cancer Classification and Biomarker Identification using Multi-Omics Data

Authors: Fadi Alharbi, Nishant Budhiraja, Aleksandar Vakanski, Boyu Zhang, Murtada K. Elbashir, Harshith Guduru, Mohanad Mohammed

Abstract: The integration of heterogeneous multi-omics datasets at a systems level remains a central challenge for developing analytical and computational models in precision cancer diagnostics. This paper introduces Multi-Omics Graph Kolmogorov-Arnold Network (MOGKAN), a deep learning framework that utilizes messenger-RNA, micro-RNA sequences, and DNA methylation samples together with Protein-Protein Interaction (PPI) networks for cancer classification across 31 different cancer types. The proposed approach combines differential gene expression with DESeq2, Linear Models for Microarray (LIMMA), and Least Absolute Shrinkage and Selection Operator (LASSO) regression to reduce multi-omics data dimensionality while preserving relevant biological features. The model architecture is based on the Kolmogorov-Arnold theorem principle and uses trainable univariate functions to enhance interpretability and feature analysis. MOGKAN achieves classification accuracy of 96.28 percent and exhibits low experimental variability in comparison to related deep learning-based models. The biomarkers identified by MOGKAN were validated as cancer-related markers through Gene Ontology (GO) and Kyoto Encyclopedia of Genes and Genomes (KEGG) enrichment analysis. By integrating multi-omics data with graph-based deep learning, our proposed approach demonstrates robust predictive performance and interpretability with potential to enhance the translation of complex multi-omics data into clinically actionable cancer diagnostics.

Function Fitting Based on Kolmogorov-Arnold Theorem and Kernel Functions

Authors: Jianpeng Liu, Qizhi Pan

Abstract: This paper proposes a unified theoretical framework based on the Kolmogorov-Arnold representation theorem and kernel methods. By analyzing the mathematical relationship among kernels, B-spline basis functions in Kolmogorov-Arnold Networks (KANs) and the inner product operation in self-attention mechanisms, we establish a kernel-based feature fitting framework that unifies the two models as linear combinations of kernel functions. Under this framework, we propose a low-rank Pseudo-Multi-Head Self-Attention module (Pseudo-MHSA), which reduces the parameter count of traditional MHSA by nearly 50\%. Furthermore, we design a Gaussian kernel multi-head self-attention variant (Gaussian-MHSA) to validate the effectiveness of nonlinear kernel functions in feature extraction. Experiments on the CIFAR-10 dataset demonstrate that Pseudo-MHSA model achieves performance comparable to the ViT model of the same dimensionality under the MAE framework and visualization analysis reveals their similarity of multi-head distribution patterns. Our code is publicly available.

Enhancing Physics-Informed Neural Networks with a Hybrid Parallel Kolmogorov-Arnold and MLP Architecture

Authors: Zuyu Xu, Bin Lv

Abstract: Neural networks have emerged as powerful tools for modeling complex physical systems, yet balancing high accuracy with computational efficiency remains a critical challenge in their convergence behavior. In this work, we propose the Hybrid Parallel Kolmogorov-Arnold Network (KAN) and Multi-Layer Perceptron (MLP) Physics-Informed Neural Network (HPKM-PINN), a novel architecture that synergistically integrates parallelized KAN and MLP branches within a unified PINN framework. The HPKM-PINN introduces a scaling factor ξ, to optimally balance the complementary strengths of KAN’s interpretable function approximation and MLP’s nonlinear feature learning, thereby enhancing predictive performance through a weighted fusion of their outputs. Through systematic numerical evaluations, we elucidate the impact of the scaling factor ξ on the model’s performance in both function approximation and partial differential equation (PDE) solving tasks. Benchmark experiments across canonical PDEs, such as the Poisson and Advection equations, demonstrate that HPKM-PINN achieves a marked decrease in loss values (reducing relative error by two orders of magnitude) compared to standalone KAN or MLP models. Furthermore, the framework exhibits numerical stability and robustness when applied to various physical systems. These findings highlight the HPKM-PINN’s ability to leverage KAN’s interpretability and MLP’s expressivity, positioning it as a versatile and scalable tool for solving complex PDE-driven problems in computational science and engineering.

Introducing the Short-Time Fourier Kolmogorov Arnold Network: A Dynamic Graph CNN Approach for Tree Species Classification in 3D Point Clouds

Authors: Said Ohamouddou, Mohamed Ohamouddou, Hanaa El Afia, Abdellatif El Afia, Rafik Lasri, Raddouane Chiheb

Abstract: Accurate classification of tree species based on Terrestrial Laser Scanning (TLS) and Airborne Laser Scanning (ALS) is essential for biodiversity conservation. While advanced deep learning models for 3D point cloud classification have demonstrated strong performance in this domain, their high complexity often hinders the development of efficient, low-computation architectures. In this paper, we introduce STFT-KAN, a novel Kolmogorov-Arnold network that integrates the Short-Time Fourier Transform (STFT), which can replace the standard linear layer with activation. We implemented STFT-KAN within a lightweight version of DGCNN, called liteDGCNN, to classify tree species using the TLS data. Our experiments show that STFT-KAN outperforms existing KAN variants by effectively balancing model complexity and performance with parameter count reduction, achieving competitive results compared to MLP-based models. Additionally, we evaluated a hybrid architecture that combines MLP in edge convolution with STFT-KAN in other layers, achieving comparable performance to MLP models while reducing the parameter count by 50% and 75% compared to other KAN-based variants. Furthermore, we compared our model to leading 3D point cloud learning approaches, demonstrating that STFT-KAN delivers competitive results compared to the state-of-the-art method PointMLP lite with an 87% reduction in parameter count.

April

Advancing Cosmological Parameter Estimation and Hubble Parameter Reconstruction with Long Short-Term Memory and Efficient-Kolmogorov-Arnold Networks

Authors: Jiaxing Cui, Marek Biesiada, Ao Liu, Cuihong Wen, Tonghua Liu, Jieci Wang

Abstract: In this work, we propose a novel approach for cosmological parameter estimation and Hubble parameter reconstruction using Long Short-Term Memory (LSTM) networks and Efficient-Kolmogorov-Arnold Networks (Ef-KAN). LSTM networks are employed to extract features from observational data, enabling accurate parameter inference and posterior distribution estimation without relying on solvable likelihood functions. This method achieves performance comparable to traditional Markov Chain Monte Carlo (MCMC) techniques, offering a computationally efficient alternative for high-dimensional parameter spaces. By sampling from the reconstructed data and comparing it with mock data, our designed LSTM constraint procedure demonstrates the superior performance of this method in terms of constraint accuracy, and effectively captures the degeneracies and correlations between the cosmological parameters. Additionally, the Ef-KAN model is introduced to reconstruct the Hubble parameter H(z) from both observational and mock data. Ef-KAN is entirely data-driven approach, free from prior assumptions, and demonstrates superior capability in modeling complex, non-linear data distributions. We validate the Ef-KAN method by reconstructing the Hubble parameter, demonstrating that H(z) can be reconstructed with high accuracy. By combining LSTM and Ef-KAN, we provide a robust framework for cosmological parameter inference and Hubble parameter reconstruction, paving the way for future research in cosmology, especially when dealing with complex datasets and high-dimensional parameter spaces.

GKAN: Explainable Diagnosis of Alzheimer’s Disease Using Graph Neural Network with Kolmogorov-Arnold Networks

Authors: Tianqi Ding, Dawei Xiang, Keith E Schubert, Liang Dong

Citation Count: 1

Abstract: Alzheimer’s Disease (AD) is a progressive neurodegenerative disorder that poses significant diagnostic challenges due to its complex etiology. Graph Convolutional Networks (GCNs) have shown promise in modeling brain connectivity for AD diagnosis, yet their reliance on linear transformations limits their ability to capture intricate nonlinear patterns in neuroimaging data. To address this, we propose GCN-KAN, a novel single-modal framework that integrates Kolmogorov-Arnold Networks (KAN) into GCNs to enhance both diagnostic accuracy and interpretability. Leveraging structural MRI data, our model employs learnable spline-based transformations to better represent brain region interactions. Evaluated on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset, GCN-KAN outperforms traditional GCNs by 4-8% in classification accuracy while providing interpretable insights into key brain regions associated with AD. This approach offers a robust and explainable tool for early AD diagnosis.

Opening the Black-Box: Symbolic Regression with Kolmogorov-Arnold Networks for Energy Applications

Authors: Nataly R. Panczyk, Omer F. Erdem, Majdi I. Radaideh

Abstract: While most modern machine learning methods offer speed and accuracy, few promise interpretability or explainability – two key features necessary for highly sensitive industries, like medicine, finance, and engineering. Using eight datasets representative of one especially sensitive industry, nuclear power, this work compares a traditional feedforward neural network (FNN) to a Kolmogorov-Arnold Network (KAN). We consider not only model performance and accuracy, but also interpretability through model architecture and explainability through a post-hoc SHAP analysis. In terms of accuracy, we find KANs and FNNs comparable across all datasets, when output dimensionality is limited. KANs, which transform into symbolic equations after training, yield perfectly interpretable models while FNNs remain black-boxes. Finally, using the post-hoc explainability results from Kernel SHAP, we find that KANs learn real, physical relations from experimental data, while FNNs simply produce statistically accurate results. Overall, this analysis finds KANs a promising alternative to traditional machine learning methods, particularly in applications requiring both accuracy and comprehensibility.

Improving Brain Disorder Diagnosis with Advanced Brain Function Representation and Kolmogorov-Arnold Networks

Authors: Tyler Ward, Abdullah-Al-Zubaer Imran

Abstract: Quantifying functional connectivity (FC), a vital metric for the diagnosis of various brain disorders, traditionally relies on the use of a pre-defined brain atlas. However, using such atlases can lead to issues regarding selection bias and lack of regard for specificity. Addressing this, we propose a novel transformer-based classification network (ABFR-KAN) with effective brain function representation to aid in diagnosing autism spectrum disorder (ASD). ABFR-KAN leverages Kolmogorov-Arnold Network (KAN) blocks replacing traditional multi-layer perceptron (MLP) components. Thorough experimentation reveals the effectiveness of ABFR-KAN in improving the diagnosis of ASD under various configurations of the model architecture. Our code is available at https://github.com/tbwa233/ABFR-KAN △ Less

DeepOHeat-v1: Efficient Operator Learning for Fast and Trustworthy Thermal Simulation and Optimization in 3D-IC Design

Authors: Xinling Yu, Ziyue Liu, Hai Li, Yixing Li, Xin Ai, Zhiyu Zeng, Ian Young, Zheng Zhang

Abstract: Thermal analysis is crucial in 3D-IC design due to increased power density and complex heat dissipation paths. Although operator learning frameworks such as DeepOHeat~\cite{liu2023deepoheat} have demonstrated promising preliminary results in accelerating thermal simulation, they face critical limitations in prediction capability for multi-scale thermal patterns, training efficiency, and trustworthiness of results during design optimization. This paper presents DeepOHeat-v1, an enhanced physics-informed operator learning framework that addresses these challenges through three key innovations. First, we integrate Kolmogorov-Arnold Networks with learnable activation functions as trunk networks, enabling an adaptive representation of multi-scale thermal patterns. This approach achieves a 1.25x and 6.29x reduction in error in two representative test cases. Second, we introduce a separable training method that decomposes the basis function along the coordinate axes, achieving 62x training speedup and 31x GPU memory reduction in our baseline case, and enabling thermal analysis at resolutions previously infeasible due to GPU memory constraints. Third, we propose a confidence score to evaluate the trustworthiness of the predicted results, and further develop a hybrid optimization workflow that combines operator learning with finite difference (FD) using Generalized Minimal Residual (GMRES) method for incremental solution refinement, enabling efficient and trustworthy thermal optimization. Experimental results demonstrate that DeepOHeat-v1 achieves accuracy comparable to optimization using high-fidelity finite difference solvers, while speeding up the entire optimization process by $70.6\times$ in our test cases, effectively minimizing the peak temperature through optimal placement of heat-generating components. Open source code is available at https://github.com/xlyu0127/DeepOHeat-v1.

Extending Cox Proportional Hazards Model with Symbolic Non-Linear Log-Risk Functions for Survival Analysis

Authors: Jiaxiang Cheng, Guoqiang Hu

Abstract: The Cox proportional hazards (CPH) model has been widely applied in survival analysis to estimate relative risks across different subjects given multiple covariates. Traditional CPH models rely on a linear combination of covariates weighted with coefficients as the log-risk function, which imposes a strong and restrictive assumption, limiting generalization. Recent deep learning methods enable non-linear log-risk functions. However, they often lack interpretability due to the end-to-end training mechanisms. The implementation of Kolmogorov-Arnold Networks (KAN) offers new possibilities for extending the CPH model with fully transparent and symbolic non-linear log-risk functions. In this paper, we introduce Generalized Cox Proportional Hazards (GCPH) model, a novel method for survival analysis that leverages KAN to enable a non-linear mapping from covariates to survival outcomes in a fully symbolic manner. GCPH maintains the interpretability of traditional CPH models while allowing for the estimation of non-linear log-risk functions. Experiments conducted on both synthetic data and various public benchmarks demonstrate that GCPH achieves competitive performance in terms of prediction accuracy and exhibits superior interpretability compared to current state-of-the-art methods.

asKAN: Active Subspace embedded Kolmogorov-Arnold Network

Authors: Zhiteng Zhou, Zhaoyue Xu, Yi Liu, Shizhao Wang

Abstract: The Kolmogorov-Arnold Network (KAN) has emerged as a promising neural network architecture for small-scale AI+Science applications. However, it suffers from inflexibility in modeling ridge functions, which is widely used in representing the relationships in physical systems. This study investigates this inflexibility through the lens of the Kolmogorov-Arnold theorem, which starts the representation of multivariate functions from constructing the univariate components rather than combining the independent variables. Our analysis reveals that incorporating linear combinations of independent variables can substantially simplify the network architecture in representing the ridge functions. Inspired by this finding, we propose active subspace embedded KAN (asKAN), a hierarchical framework that synergizes KAN’s function representation with active subspace methodology. The architecture strategically embeds active subspace detection between KANs, where the active subspace method is used to identify the primary ridge directions and the independent variables are adaptively projected onto these critical dimensions. The proposed asKAN is implemented in an iterative way without increasing the number of neurons in the original KAN. The proposed method is validated through function fitting, solving the Poisson equation, and reconstructing sound field. Compared with KAN, asKAN significantly reduces the error using the same network architecture. The results suggest that asKAN enhances the capability of KAN in fitting and solving equations in the form of ridge functions.

Solving the fully nonlinear Monge-Ampère equation using the Legendre-Kolmogorov-Arnold Network method

Authors: Bingcheng Hu, Lixiang Jin, Zhaoxiang Li

Abstract: In this paper, we propose a novel neural network framework, the Legendre-Kolmogorov-Arnold Network (Legendre-KAN) method, designed to solve fully nonlinear Monge-Ampère equations with Dirichlet boundary conditions. The architecture leverages the orthogonality of Legendre polynomials as basis functions, significantly enhancing both convergence speed and solution accuracy compared to traditional methods. Furthermore, the Kolmogorov-Arnold representation theorem provides a strong theoretical foundation for the interpretability and optimization of the network. We demonstrate the effectiveness of the proposed method through numerical examples, involving both smooth and singular solutions in various dimensions. This work not only addresses the challenges of solving high-dimensional and singular Monge-Ampère equations but also highlights the potential of neural network-based approaches for complex partial differential equations. Additionally, the method is applied to the optimal transport problem in image mapping, showcasing its practical utility in geometric image transformation. This approach is expected to pave the way for further enhancement of KAN-based applications and numerical solutions of PDEs across a wide range of scientific and engineering fields.

KAN-SAM: Kolmogorov-Arnold Network Guided Segment Anything Model for RGB-T Salient Object Detection

Authors: Xingyuan Li, Ruichao Hou, Tongwei Ren, Gangshan Wu

Abstract: Existing RGB-thermal salient object detection (RGB-T SOD) methods aim to identify visually significant objects by leveraging both RGB and thermal modalities to enable robust performance in complex scenarios, but they often suffer from limited generalization due to the constrained diversity of available datasets and the inefficiencies in constructing multi-modal representations. In this paper, we propose a novel prompt learning-based RGB-T SOD method, named KAN-SAM, which reveals the potential of visual foundational models for RGB-T SOD tasks. Specifically, we extend Segment Anything Model 2 (SAM2) for RGB-T SOD by introducing thermal features as guiding prompts through efficient and accurate Kolmogorov-Arnold Network (KAN) adapters, which effectively enhance RGB representations and improve robustness. Furthermore, we introduce a mutually exclusive random masking strategy to reduce reliance on RGB data and improve generalization. Experimental results on benchmarks demonstrate superior performance over the state-of-the-art methods.

Physics-informed KAN PointNet: Deep learning for simultaneous solutions to inverse problems in incompressible flow on numerous irregular geometries

Authors: Ali Kashefi, Tapan Mukerji

Abstract: Kolmogorov-Arnold Networks (KANs) have gained attention as an alternative to traditional multilayer perceptrons (MLPs) for deep learning applications in computational physics, particularly for solving inverse problems with sparse data, as exemplified by the physics-informed Kolmogorov-Arnold network (PIKAN). However, the capability of KANs to simultaneously solve inverse problems over multiple irregular geometries within a single training run remains unexplored. To address this gap, we introduce the physics-informed Kolmogorov-Arnold PointNet (PI-KAN-PointNet), in which shared KANs are integrated into the PointNet architecture to capture the geometric features of computational domains. The loss function comprises the squared residuals of the governing equations, computed via automatic differentiation, along with sparse observations and partially known boundary conditions. We construct shared KANs using Jacobi polynomials and investigate their performance by considering Jacobi polynomials of different degrees and types in terms of both computational cost and prediction accuracy. As a benchmark test case, we consider natural convection in a square enclosure with a cylinder, where the cylinder’s shape varies across a dataset of 135 geometries. PI-KAN-PointNet offers two main advantages. First, it overcomes the limitation of current PIKANs, which are restricted to solving only a single computational domain per training run, thereby reducing computational costs. Second, when comparing the performance of PI-KAN-PointNet with that of the physics-informed PointNet using MLPs, we observe that, with approximately the same number of trainable parameters and comparable computational cost in terms of the number of epochs, training time per epoch, and memory usage, PI-KAN-PointNet yields more accurate predictions, particularly for values on unknown boundary conditions involving nonsmooth geometries.

TabKAN: Advancing Tabular Data Analysis using Kolmogorov-Arnold Network

Authors: Ali Eslamian, Alireza Afzal Aghaei, Qiang Cheng

Abstract: Tabular data analysis presents unique challenges that arise from heterogeneous feature types, missing values, and complex feature interactions. While traditional machine learning methods like gradient boosting often outperform deep learning, recent advancements in neural architectures offer promising alternatives. In this study, we introduce TabKAN, a novel framework for tabular data modeling based on Kolmogorov-Arnold Networks (KANs). Unlike conventional deep learning models, KANs use learnable activation functions on edges, which improves both interpretability and training efficiency. TabKAN incorporates modular KAN-based architectures designed for tabular analysis and proposes a transfer learning framework for knowledge transfer across domains. Furthermore, we develop a model-specific interpretability approach that reduces reliance on post hoc explanations. Extensive experiments on public datasets show that TabKAN achieves superior performance in supervised learning and significantly outperforms classical and Transformer-based models in binary and multi-class classification. The results demonstrate the potential of KAN-based architectures to bridge the gap between traditional machine learning and deep learning for structured data.

Representation Meets Optimization: Training PINNs and PIKANs for Gray-Box Discovery in Systems Pharmacology

Authors: Nazanin Ahmadi Daryakenari, Khemraj Shukla, George Em Karniadakis

Abstract: Physics-Informed Kolmogorov-Arnold Networks (PIKANs) are gaining attention as an effective counterpart to the original multilayer perceptron-based Physics-Informed Neural Networks (PINNs). Both representation models can address inverse problems and facilitate gray-box system identification. However, a comprehensive understanding of their performance in terms of accuracy and speed remains underexplored. In particular, we introduce a modified PIKAN architecture, tanh-cPIKAN, which is based on Chebyshev polynomials for parametrization of the univariate functions with an extra nonlinearity for enhanced performance. We then present a systematic investigation of how choices of the optimizer, representation, and training configuration influence the performance of PINNs and PIKANs in the context of systems pharmacology modeling. We benchmark a wide range of first-order, second-order, and hybrid optimizers, including various learning rate schedulers. We use the new Optax library to identify the most effective combinations for learning gray-boxes under ill-posed, non-unique, and data-sparse conditions. We examine the influence of model architecture (MLP vs. KAN), numerical precision (single vs. double), the need for warm-up phases for second-order methods, and sensitivity to the initial learning rate. We also assess the optimizer scalability for larger models and analyze the trade-offs introduced by JAX in terms of computational efficiency and numerical accuracy. Using two representative systems pharmacology case studies - a pharmacokinetics model and a chemotherapy drug-response model - we offer practical guidance on selecting optimizers and representation models/architectures for robust and efficient gray-box discovery. Our findings provide actionable insights for improving the training of physics-informed networks in biomedical applications and beyond.

A Case for Kolmogorov-Arnold Networks in Prefetching: Towards Low-Latency, Generalizable ML-Based Prefetchers

Authors: Dhruv Kulkarni, Bharat Bhammar, Henil Thaker, Pranav Dhobi, R. P. Gohil, Sai Manoj Pudukotai Dinkarrao

Abstract: The memory wall problem arises due to the disparity between fast processors and slower memory, causing significant delays in data access, even more so on edge devices. Data prefetching is a key strategy to address this, with traditional methods evolving to incorporate Machine Learning (ML) for improved accuracy. Modern prefetchers must balance high accuracy with low latency to further practicality. We explore the applicability of utilizing Kolmogorov-Arnold Networks (KAN) with learnable activation functions,a prefetcher we implemented called KANBoost, to further this aim. KANs are a novel, state-of-the-art model that work on breaking down continuous, bounded multi-variate functions into functions of their constituent variables, and use these constitutent functions as activations on each individual neuron. KANBoost predicts the next memory access by modeling deltas between consecutive addresses, offering a balance of accuracy and efficiency to mitigate the memory wall problem with minimal overhead, instead of relying on address-correlation prefetching. Initial results indicate that KAN-based prefetching reduces inference latency (18X lower than state-of-the-art ML prefetchers) while achieving moderate IPC improvements (2.5\% over no-prefetching). While KANs still face challenges in capturing long-term dependencies, we propose that future research should explore hybrid models that combine KAN efficiency with stronger sequence modeling techniques, paving the way for practical ML-based prefetching in edge devices and beyond.

GPT Meets Graphs and KAN Splines: Testing Novel Frameworks on Multitask Fine-Tuned GPT-2 with LoRA

Authors: Gabriel Bo, Marc Bernardino, Justin Gu

Abstract: We explore the potential of integrating learnable and interpretable modules–specifically Kolmogorov-Arnold Networks (KAN) and graph-based representations–within a pre-trained GPT-2 model to enhance multi-task learning accuracy. Motivated by the recent surge in using KAN and graph attention (GAT) architectures in chain-of-thought (CoT) models and debates over their benefits compared to simpler architectures like MLPs, we begin by enhancing a standard self-attention transformer using Low-Rank Adaptation (LoRA), fine-tuning hyperparameters, and incorporating L2 regularization. This approach yields significant improvements. To further boost interpretability and richer representations, we develop two variants that attempt to improve the standard KAN and GAT: Graph LoRA and Hybrid-KAN LoRA (Learnable GPT). However, systematic evaluations reveal that neither variant outperforms the optimized LoRA-enhanced transformer, which achieves 55.249% accuracy on the SST test set, 99.18% on the CFIMDB dev set, and 89.9% paraphrase detection test accuracy. On sonnet generation, we get a CHRF score of 42.097. These findings highlight that efficient parameter adaptation via LoRA remains the most effective strategy for our tasks: sentiment analysis, paraphrase detection, and sonnet generation.

MLPs and KANs for data-driven learning in physical problems: A performance comparison

Authors: Raghav Pant, Sikan Li, Xingjian Li, Hassan Iqbal, Krishna Kumar

Abstract: There is increasing interest in solving partial differential equations (PDEs) by casting them as machine learning problems. Recently, there has been a spike in exploring Kolmogorov-Arnold Networks (KANs) as an alternative to traditional neural networks represented by Multi-Layer Perceptrons (MLPs). While showing promise, their performance advantages in physics-based problems remain largely unexplored. Several critical questions persist: Can KANs capture complex physical dynamics and under what conditions might they outperform traditional architectures? In this work, we present a comparative study of KANs and MLPs for learning physical systems governed by PDEs. We assess their performance when applied in deep operator networks (DeepONet) and graph network-based simulators (GNS), and test them on physical problems that vary significantly in scale and complexity. Drawing inspiration from the Kolmogorov Representation Theorem, we examine the behavior of KANs and MLPs across shallow and deep network architectures. Our results reveal that although KANs do not consistently outperform MLPs when configured as deep neural networks, they demonstrate superior expressiveness in shallow network settings, significantly outpacing MLPs in accuracy over our test cases. This suggests that KANs are a promising choice, offering a balance of efficiency and accuracy in applications involving physical systems.

Towards Explainable Fusion and Balanced Learning in Multimodal Sentiment Analysis

Authors: Miaosen Luo, Yuncheng Jiang, Sijie Mai

Abstract: Multimodal Sentiment Analysis (MSA) faces two critical challenges: the lack of interpretability in the decision logic of multimodal fusion and modality imbalance caused by disparities in inter-modal information density. To address these issues, we propose KAN-MCP, a novel framework that integrates the interpretability of Kolmogorov-Arnold Networks (KAN) with the robustness of the Multimodal Clean Pareto (MCPareto) framework. First, KAN leverages its univariate function decomposition to achieve transparent analysis of cross-modal interactions. This structural design allows direct inspection of feature transformations without relying on external interpretation tools, thereby ensuring both high expressiveness and interpretability. Second, the proposed MCPareto enhances robustness by addressing modality imbalance and noise interference. Specifically, we introduce the Dimensionality Reduction and Denoising Modal Information Bottleneck (DRD-MIB) method, which jointly denoises and reduces feature dimensionality. This approach provides KAN with discriminative low-dimensional inputs to reduce the modeling complexity of KAN while preserving critical sentiment-related information. Furthermore, MCPareto dynamically balances gradient contributions across modalities using the purified features output by DRD-MIB, ensuring lossless transmission of auxiliary signals and effectively alleviating modality imbalance. This synergy of interpretability and robustness not only achieves superior performance on benchmark datasets such as CMU-MOSI, CMU-MOSEI, and CH-SIMS v2 but also offers an intuitive visualization interface through KAN’s interpretable architecture. Our code is released on https://github.com/LuoMSen/KAN-MCP.

Approximation Bounds for Transformer Networks with Application to Regression

Authors: Yuling Jiao, Yanming Lai, Defeng Sun, Yang Wang, Bokai Yan

Abstract: We explore the approximation capabilities of Transformer networks for Hölder and Sobolev functions, and apply these results to address nonparametric regression estimation with dependent observations. First, we establish novel upper bounds for standard Transformer networks approximating sequence-to-sequence mappings whose component functions are Hölder continuous with smoothness index $γ\in (0,1]$. To achieve an approximation error $\varepsilon$ under the $L^p$-norm for $p \in [1, \infty]$, it suffices to use a fixed-depth Transformer network whose total number of parameters scales as $\varepsilon^{-d_x n / γ}$. This result not only extends existing findings to include the case $p = \infty$, but also matches the best known upper bounds on number of parameters previously obtained for fixed-depth FNNs and RNNs. Similar bounds are also derived for Sobolev functions. Second, we derive explicit convergence rates for the nonparametric regression problem under various $β$-mixing data assumptions, which allow the dependence between observations to weaken over time. Our bounds on the sample complexity impose no constraints on weight magnitudes. Lastly, we propose a novel proof strategy to establish approximation bounds, inspired by the Kolmogorov-Arnold representation theorem. We show that if the self-attention layer in a Transformer can perform column averaging, the network can approximate sequence-to-sequence Hölder functions, offering new insights into the interpretability of self-attention mechanisms.

ChemKANs for Combustion Chemistry Modeling and Acceleration

Authors: Benjamin C. Koenig, Suyong Kim, Sili Deng

Citation Count: 1

Abstract: Efficient chemical kinetic model inference and application in combustion are challenging due to large ODE systems and widely separated time scales. Machine learning techniques have been proposed to streamline these models, though strong nonlinearity and numerical stiffness combined with noisy data sources make their application challenging. Here, we introduce ChemKANs, a novel neural network framework with applications both in model inference and simulation acceleration for combustion chemistry. ChemKAN’s novel structure augments the generic Kolmogorov Arnold Network Ordinary Differential Equations (KAN-ODEs) with knowledge of the information flow through the relevant kinetic and thermodynamic laws. This chemistry-specific structure combined with the expressivity and rapid neural scaling of the underlying KAN-ODE algorithm instills in ChemKANs a strong inductive bias, streamlined training, and higher accuracy predictions compared to standard benchmarks, while facilitating parameter sparsity through shared information across all inputs and outputs. In a model inference investigation, we benchmark the robustness of ChemKANs to sparse data containing up to 15% added noise, and superfluously large network parameterizations. We find that ChemKANs exhibit no overfitting or model degradation in any of these training cases, demonstrating significant resilience to common deep learning failure modes. Next, we find that a remarkably parameter-lean ChemKAN (344 parameters) can accurately represent hydrogen combustion chemistry, providing a 2x acceleration over the detailed chemistry in a solver that is generalizable to larger-scale turbulent flow simulations. These demonstrations indicate the potential for ChemKANs as robust, expressive, and efficient tools for model inference and simulation acceleration for combustion physics and chemical kinetics.

Transformers Can Overcome the Curse of Dimensionality: A Theoretical Study from an Approximation Perspective

Authors: Yuling Jiao, Yanming Lai, Yang Wang, Bokai Yan

Abstract: The Transformer model is widely used in various application areas of machine learning, such as natural language processing. This paper investigates the approximation of the Hölder continuous function class $\mathcal{H}_{Q}^β\left([0,1]^{d\times n},\mathbb{R}^{d\times n}\right)$ by Transformers and constructs several Transformers that can overcome the curse of dimensionality. These Transformers consist of one self-attention layer with one head and the softmax function as the activation function, along with several feedforward layers. For example, to achieve an approximation accuracy of $ε$, if the activation functions of the feedforward layers in the Transformer are ReLU and floor, only $\mathcal{O}\left(\log\frac{1}ε\right)$ layers of feedforward layers are needed, with widths of these layers not exceeding $\mathcal{O}\left(\frac{1}{ε^{2/β}}\log\frac{1}ε\right)$. If other activation functions are allowed in the feedforward layers, the width of the feedforward layers can be further reduced to a constant. These results demonstrate that Transformers have a strong expressive capability. The construction in this paper is based on the Kolmogorov-Arnold Representation Theorem and does not require the concept of contextual mapping, hence our proof is more intuitively clear compared to previous Transformer approximation works. Additionally, the translation technique proposed in this paper helps to apply the previous approximation results of feedforward neural networks to Transformer research.

KAN or MLP? Point Cloud Shows the Way Forward

Authors: Yan Shi, Qingdong He, Yijun Liu, Xiaoyu Liu, Jingyong Su

Abstract: Multi-Layer Perceptrons (MLPs) have become one of the fundamental architectural component in point cloud analysis due to its effective feature learning mechanism. However, when processing complex geometric structures in point clouds, MLPs’ fixed activation functions struggle to efficiently capture local geometric features, while suffering from poor parameter efficiency and high model redundancy. In this paper, we propose PointKAN, which applies Kolmogorov-Arnold Networks (KANs) to point cloud analysis tasks to investigate their efficacy in hierarchical feature representation. First, we introduce a Geometric Affine Module (GAM) to transform local features, improving the model’s robustness to geometric variations. Next, in the Local Feature Processing (LFP), a parallel structure extracts both group-level features and global context, providing a rich representation of both fine details and overall structure. Finally, these features are combined and processed in the Global Feature Processing (GFP). By repeating these operations, the receptive field gradually expands, enabling the model to capture complete geometric information of the point cloud. To overcome the high parameter counts and computational inefficiency of standard KANs, we develop Efficient-KANs in the PointKAN-elite variant, which significantly reduces parameters while maintaining accuracy. Experimental results demonstrate that PointKAN outperforms PointMLP on benchmark datasets such as ModelNet40, ScanObjectNN, and ShapeNetPart, with particularly strong performance in Few-shot Learning task. Additionally, PointKAN achieves substantial reductions in parameter counts and computational complexity (FLOPs). This work highlights the potential of KANs-based architectures in 3D vision and opens new avenues for research in point cloud understanding.

Efficient Implicit Neural Compression of Point Clouds via Learnable Activation in Latent Space

Authors: Yichi Zhang, Qianqian Yang

Abstract: Implicit Neural Representations (INRs), also known as neural fields, have emerged as a powerful paradigm in deep learning, parameterizing continuous spatial fields using coordinate-based neural networks. In this paper, we propose \textbf{PICO}, an INR-based framework for static point cloud compression. Unlike prevailing encoder-decoder paradigms, we decompose the point cloud compression task into two separate stages: geometry compression and attribute compression, each with distinct INR optimization objectives. Inspired by Kolmogorov-Arnold Networks (KANs), we introduce a novel network architecture, \textbf{LeAFNet}, which leverages learnable activation functions in the latent space to better approximate the target signal’s implicit function. By reformulating point cloud compression as neural parameter compression, we further improve compression efficiency through quantization and entropy coding. Experimental results demonstrate that \textbf{LeAFNet} outperforms conventional MLPs in INR-based point cloud compression. Furthermore, \textbf{PICO} achieves superior geometry compression performance compared to the current MPEG point cloud compression standard, yielding an average improvement of $4.92$ dB in D1 PSNR. In joint geometry and attribute compression, our approach exhibits highly competitive results, with an average PCQM gain of $2.7 \times 10^{-3}$.

Approximation Rates in Besov Norms and Sample-Complexity of Kolmogorov-Arnold Networks with Residual Connections

Authors: Anastasis Kratsios, Bum Jun Kim, Takashi Furuya

Abstract: Inspired by the Kolmogorov-Arnold superposition theorem, Kolmogorov-Arnold Networks (KANs) have recently emerged as an improved backbone for most deep learning frameworks, promising more adaptivity than their multilayer perceptron (MLP) predecessor by allowing for trainable spline-based activation functions. In this paper, we probe the theoretical foundations of the KAN architecture by showing that it can optimally approximate any Besov function in $B^{s}{p,q}(\mathcal{X})$ on a bounded open, or even fractal, domain $\mathcal{X}$ in $\mathbb{R}^d$ at the optimal approximation rate with respect to any weaker Besov norm $B^α{p,q}(\mathcal{X})$; where $α< s$. We complement our approximation result with a statistical guarantee by bounding the pseudodimension of the relevant class of Res-KANs. As an application of the latter, we directly deduce a dimension-free estimate on the sample complexity of a residual KAN model when learning a function of Besov regularity from $N$ i.i.d. noiseless samples, showing that KANs can learn the smooth maps which they can approximate.

Conformalized-KANs: Uncertainty Quantification with Coverage Guarantees for Kolmogorov-Arnold Networks (KANs) in Scientific Machine Learning

Authors: Amirhossein Mollaali, Christian Bolivar Moya, Amanda A. Howard, Alexander Heinlein, Panos Stinis, Guang Lin

Citation Count: 1

Abstract: This paper explores uncertainty quantification (UQ) methods in the context of Kolmogorov-Arnold Networks (KANs). We apply an ensemble approach to KANs to obtain a heuristic measure of UQ, enhancing interpretability and robustness in modeling complex functions. Building on this, we introduce Conformalized-KANs, which integrate conformal prediction, a distribution-free UQ technique, with KAN ensembles to generate calibrated prediction intervals with guaranteed coverage. Extensive numerical experiments are conducted to evaluate the effectiveness of these methods, focusing particularly on the robustness and accuracy of the prediction intervals under various hyperparameter settings. We show that the conformal KAN predictions can be applied to recent extensions of KANs, including Finite Basis KANs (FBKANs) and multifideilty KANs (MFKANs). The results demonstrate the potential of our approaches to improve the reliability and applicability of KANs in scientific machine learning.

DAE-KAN: A Kolmogorov-Arnold Network Model for High-Index Differential-Algebraic Equations

Authors: Kai Luo, Juan Tang, Mingchao Cai, Xiaoqing Zeng, Manqi Xie, Ming Yan

Abstract: Kolmogorov-Arnold Networks (KANs) have emerged as a promising alternative to Multi-layer Perceptrons (MLPs) due to their superior function-fitting abilities in data-driven modeling. In this paper, we propose a novel framework, DAE-KAN, for solving high-index differential-algebraic equations (DAEs) by integrating KANs with Physics-Informed Neural Networks (PINNs). This framework not only preserves the ability of traditional PINNs to model complex systems governed by physical laws but also enhances their performance by leveraging the function-fitting strengths of KANs. Numerical experiments demonstrate that for DAE systems ranging from index-1 to index-3, DAE-KAN reduces the absolute errors of both differential and algebraic variables by 1 to 2 orders of magnitude compared to traditional PINNs. To assess the effectiveness of this approach, we analyze the drift-off error and find that both PINNs and DAE-KAN outperform classical numerical methods in controlling this phenomenon. Our results highlight the potential of neural network methods, particularly DAE-KAN, in solving high-index DAEs with substantial computational accuracy and generalization, offering a promising solution for challenging partial differential-algebraic equations.

iTFKAN: Interpretable Time Series Forecasting with Kolmogorov-Arnold Network

Authors: Ziran Liang, Rui An, Wenqi Fan, Yanghui Rao, Yuxuan Liang

Abstract: As time evolves, data within specific domains exhibit predictability that motivates time series forecasting to predict future trends from historical data. However, current deep forecasting methods can achieve promising performance but generally lack interpretability, hindering trustworthiness and practical deployment in safety-critical applications such as auto-driving and healthcare. In this paper, we propose a novel interpretable model, iTFKAN, for credible time series forecasting. iTFKAN enables further exploration of model decision rationales and underlying data patterns due to its interpretability achieved through model symbolization. Besides, iTFKAN develops two strategies, prior knowledge injection, and time-frequency synergy learning, to effectively guide model learning under complex intertwined time series data. Extensive experimental results demonstrated that iTFKAN can achieve promising forecasting performance while simultaneously possessing high interpretive capabilities.

FiberKAN: Kolmogorov-Arnold Networks for Nonlinear Fiber Optics

Authors: Xiaotian Jiang, Min Zhang, Xiao Luo, Zelai Yu, Yiming Meng, Danshi Wang

Venue: Journal of Lightwave Technology

Abstract: Scientific discovery and dynamic characterization of the physical system play a critical role in understanding, learning, and modeling the physical phenomena and behaviors in various fields. Although theories and laws of many system dynamics have been derived from rigorous first principles, there are still a considerable number of complex dynamics that have not yet been discovered and characterized, which hinders the progress of science in corresponding fields. To address these challenges, artificial intelligence for science (AI4S) has emerged as a burgeoning research field. In this paper, a Kolmogorov-Arnold Network (KAN)-based AI4S framework named FiberKAN is proposed for scientific discovery and dynamic characterization of nonlinear fiber optics. Unlike the classic multi-layer perceptron (MLP) structure, the trainable and transparent activation functions in KAN make the network have stronger physical interpretability and nonlinear characterization abilities. Multiple KANs are established for fiber-optic system dynamics under various physical effects. Results show that KANs can well discover and characterize the explicit, implicit, and non-analytical solutions under different effects, and achieve better performance than MLPs with the equivalent scale of trainable parameters. Moreover, the effectiveness, computational cost, interactivity, noise resistance, transfer learning ability, and comparison between related algorithms in fiber-optic systems are also studied and analyzed. This work highlights the transformative potential of KAN, establishing it as a pioneering paradigm in AI4S that propels advancements in nonlinear fiber optics, and fosters groundbreaking innovations across a broad spectrum of scientific and engineering disciplines.

A Unified Benchmark of Federated Learning with Kolmogorov-Arnold Networks for Medical Imaging

Authors: Youngjoon Lee, Jinu Gong, Joonhyuk Kang

Citation Count: 1

Abstract: Federated Learning (FL) enables model training across decentralized devices without sharing raw data, thereby preserving privacy in sensitive domains like healthcare. In this paper, we evaluate Kolmogorov-Arnold Networks (KAN) architectures against traditional MLP across six state-of-the-art FL algorithms on a blood cell classification dataset. Notably, our experiments demonstrate that KAN can effectively replace MLP in federated environments, achieving superior performance with simpler architectures. Furthermore, we analyze the impact of key hyperparameters-grid size and network architecture-on KAN performance under varying degrees of Non-IID data distribution. In addition, our ablation studies reveal that optimizing KAN width while maintaining minimal depth yields the best performance in federated settings. As a result, these findings establish KAN as a promising alternative for privacy-preserving medical imaging applications in distributed healthcare. To the best of our knowledge, this is the first comprehensive benchmark of KAN in FL settings for medical imaging task.

May

Anant-Net: Breaking the Curse of Dimensionality with Scalable and Interpretable Neural Surrogate for High-Dimensional PDEs

Authors: Sidharth S. Menon, Ameya D. Jagtap

Abstract: High-dimensional partial differential equations (PDEs) arise in diverse scientific and engineering applications but remain computationally intractable due to the curse of dimensionality. Traditional numerical methods struggle with the exponential growth in computational complexity, particularly on hypercubic domains, where the number of required collocation points increases rapidly with dimensionality. Here, we introduce Anant-Net, an efficient neural surrogate that overcomes this challenge, enabling the solution of PDEs in high dimensions. Unlike hyperspheres, where the internal volume diminishes as dimensionality increases, hypercubes retain or expand their volume (for unit or larger length), making high-dimensional computations significantly more demanding. Anant-Net efficiently incorporates high-dimensional boundary conditions and minimizes the PDE residual at high-dimensional collocation points. To enhance interpretability, we integrate Kolmogorov-Arnold networks into the Anant-Net architecture. We benchmark Anant-Net’s performance on several linear and nonlinear high-dimensional equations, including the Poisson, Sine-Gordon, and Allen-Cahn equations, demonstrating high accuracy and robustness across randomly sampled test points from high-dimensional space. Importantly, Anant-Net achieves these results with remarkable efficiency, solving 300-dimensional problems on a single GPU within a few hours. We also compare Anant-Net’s results for accuracy and runtime with other state-of-the-art methods. Our findings establish Anant-Net as an accurate, interpretable, and scalable framework for efficiently solving high-dimensional PDEs.

Novel Extraction of Discriminative Fine-Grained Feature to Improve Retinal Vessel Segmentation

Authors: Shuang Zeng, Chee Hong Lee, Micky C Nnamdi, Wenqi Shi, J Ben Tamo, Lei Zhu, Hangzhou He, Xinliang Zhang, Qian Chen, May D. Wang, Yanye Lu, Qiushi Ren

Abstract: Retinal vessel segmentation is a vital early detection method for several severe ocular diseases. Despite significant progress in retinal vessel segmentation with the advancement of Neural Networks, there are still challenges to overcome. Specifically, retinal vessel segmentation aims to predict the class label for every pixel within a fundus image, with a primary focus on intra-image discrimination, making it vital for models to extract more discriminative features. Nevertheless, existing methods primarily focus on minimizing the difference between the output from the decoder and the label, but ignore fully using feature-level fine-grained representations from the encoder. To address these issues, we propose a novel Attention U-shaped Kolmogorov-Arnold Network named AttUKAN along with a novel Label-guided Pixel-wise Contrastive Loss for retinal vessel segmentation. Specifically, we implement Attention Gates into Kolmogorov-Arnold Networks to enhance model sensitivity by suppressing irrelevant feature activations and model interpretability by non-linear modeling of KAN blocks. Additionally, we also design a novel Label-guided Pixel-wise Contrastive Loss to supervise our proposed AttUKAN to extract more discriminative features by distinguishing between foreground vessel-pixel pairs and background pairs. Experiments are conducted across four public datasets including DRIVE, STARE, CHASE_DB1, HRF and our private dataset. AttUKAN achieves F1 scores of 82.50%, 81.14%, 81.34%, 80.21% and 80.09%, along with MIoU scores of 70.24%, 68.64%, 68.59%, 67.21% and 66.94% in the above datasets, which are the highest compared to 11 networks for retinal vessel segmentation. Quantitative and qualitative results show that our AttUKAN achieves state-of-the-art performance and outperforms existing retinal vessel segmentation methods. Our code will be available at https://github.com/stevezs315/AttUKAN.

Hyb-KAN ViT: Hybrid Kolmogorov-Arnold Networks Augmented Vision Transformer

Authors: Sainath Dey, Mitul Goswami, Jashika Sethi, Prasant Kumar Pattnaik

Abstract: This study addresses the inherent limitations of Multi-Layer Perceptrons (MLPs) in Vision Transformers (ViTs) by introducing Hybrid Kolmogorov-Arnold Network (KAN)-ViT (Hyb-KAN ViT), a novel framework that integrates wavelet-based spectral decomposition and spline-optimized activation functions, prior work has failed to focus on the prebuilt modularity of the ViT architecture and integration of edge detection capabilities of Wavelet functions. We propose two key modules: Efficient-KAN (Eff-KAN), which replaces MLP layers with spline functions and Wavelet-KAN (Wav-KAN), leveraging orthogonal wavelet transforms for multi-resolution feature extraction. These modules are systematically integrated in ViT encoder layers and classification heads to enhance spatial-frequency modeling while mitigating computational bottlenecks. Experiments on ImageNet-1K (Image Recognition), COCO (Object Detection and Instance Segmentation), and ADE20K (Semantic Segmentation) demonstrate state-of-the-art performance with Hyb-KAN ViT. Ablation studies validate the efficacy of wavelet-driven spectral priors in segmentation and spline-based efficiency in detection tasks. The framework establishes a new paradigm for balancing parameter efficiency and multi-scale representation in vision architectures.

Prediction via Shapley Value Regression

Authors: Amr Alkhatib, Roman Bresson, Henrik Boström, Michalis Vazirgiannis

Abstract: Shapley values have several desirable, theoretically well-supported, properties for explaining black-box model predictions. Traditionally, Shapley values are computed post-hoc, leading to additional computational cost at inference time. To overcome this, a novel method, called ViaSHAP, is proposed, that learns a function to compute Shapley values, from which the predictions can be derived directly by summation. Two approaches to implement the proposed method are explored; one based on the universal approximation theorem and the other on the Kolmogorov-Arnold representation theorem. Results from a large-scale empirical investigation are presented, showing that ViaSHAP using Kolmogorov-Arnold Networks performs on par with state-of-the-art algorithms for tabular data. It is also shown that the explanations of ViaSHAP are significantly more accurate than the popular approximator FastSHAP on both tabular data and images.

OccuEMBED: Occupancy Extraction Merged with Building Energy Disaggregation for Occupant-Responsive Operation at Scale

Authors: Yufei Zhang, Andrew Sonta

Abstract: Buildings account for a significant share of global energy consumption and emissions, making it critical to operate them efficiently. As electricity grids become more volatile with renewable penetration, buildings must provide flexibility to support grid stability. Building automation plays a key role in enhancing efficiency and flexibility via centralized operations, but it must prioritize occupant-centric strategies to balance energy and comfort targets. However, incorporating occupant information into large-scale, centralized building operations remains challenging due to data limitations. We investigate the potential of using whole-building smart meter data to infer both occupancy and system operations. Integrating these insights into data-driven building energy analysis allows more occupant-centric energy-saving and flexibility at scale. Specifically, we propose OccuEMBED, a unified framework for occupancy inference and system-level load analysis. It combines two key components: a probabilistic occupancy profile generator, and a controllable and interpretable load disaggregator supported by Kolmogorov-Arnold Networks (KAN). This design embeds knowledge of occupancy patterns and load-occupancy-weather relationships into deep learning models. We conducted comprehensive evaluations to demonstrate its effectiveness across synthetic and real-world datasets compared to various occupancy inference baselines. OccuEMBED always achieved average F1 scores above 0.8 in discrete occupancy inference and RMSE within 0.1-0.2 for continuous occupancy ratios. We further demonstrate how OccuEMBED integrates with building load monitoring platforms to display occupancy profiles, analyze system-level operations, and inform occupant-responsive strategies. Our model lays a robust foundation in scaling occupant-centric building management systems to meet the challenges of an evolving energy system.

Improving Generalizability of Kolmogorov-Arnold Networks via Error-Correcting Output Codes

Authors: Youngjoon Lee, Jinu Gong, Joonhyuk Kang

Abstract: Kolmogorov-Arnold Networks (KAN) offer universal function approximation using univariate spline compositions without nonlinear activations. In this work, we integrate Error-Correcting Output Codes (ECOC) into the KAN framework to transform multi-class classification into multiple binary tasks, improving robustness via Hamming distance decoding. Our proposed KAN with ECOC framework outperforms vanilla KAN on a challenging blood cell classification dataset, achieving higher accuracy across diverse hyperparameter settings. Ablation studies further confirm that ECOC consistently enhances performance across FastKAN and FasterKAN variants. These results demonstrate that ECOC integration significantly boosts KAN generalizability in critical healthcare AI applications. To the best of our knowledge, this is the first work of ECOC with KAN for enhancing multi-class medical image classification performance.

Mixer-Informer-Based Two-Stage Transfer Learning for Long-Sequence Load Forecasting in Newly Constructed Electric Vehicle Charging Stations

Authors: Zhenhua Zhou, Bozhen Jiang, Qin Wang

Abstract: The rapid rise in electric vehicle (EV) adoption demands precise charging station load forecasting, challenged by long-sequence temporal dependencies and limited data in new facilities. This study proposes MIK-TST, a novel two-stage transfer learning framework integrating Mixer, Informer, and Kolmogorov-Arnold Networks (KAN). The Mixer fuses multi-source features, Informer captures long-range dependencies via ProbSparse attention, and KAN enhances nonlinear modeling with learnable activation functions. Pre-trained on extensive data and fine-tuned on limited target data, MIK-TST achieves 4% and 8% reductions in MAE and MSE, respectively, outperforming baselines on a dataset of 26 charging stations in Boulder, USA. This scalable solution enhances smart grid efficiency and supports sustainable EV infrastructure expansion.

Enhancing Federated Learning with Kolmogorov-Arnold Networks: A Comparative Study Across Diverse Aggregation Strategies

Authors: Yizhou Ma, Zhuoqin Yang, Luis-Daniel Ibáñez

Abstract: Multilayer Perceptron (MLP), as a simple yet powerful model, continues to be widely used in classification and regression tasks. However, traditional MLPs often struggle to efficiently capture nonlinear relationships in load data when dealing with complex datasets. Kolmogorov-Arnold Networks (KAN), inspired by the Kolmogorov-Arnold representation theorem, have shown promising capabilities in modeling complex nonlinear relationships. In this study, we explore the performance of KANs within federated learning (FL) frameworks and compare them to traditional Multilayer Perceptrons. Our experiments, conducted across four diverse datasets demonstrate that KANs consistently outperform MLPs in terms of accuracy, stability, and convergence efficiency. KANs exhibit remarkable robustness under varying client numbers and non-IID data distributions, maintaining superior performance even as client heterogeneity increases. Notably, KANs require fewer communication rounds to converge compared to MLPs, highlighting their efficiency in FL scenarios. Additionally, we evaluate multiple parameter aggregation strategies, with trimmed mean and FedProx emerging as the most effective for optimizing KAN performance. These findings establish KANs as a robust and scalable alternative to MLPs for federated learning tasks, paving the way for their application in decentralized and privacy-preserving environments.

Symbolic Regression with Multimodal Large Language Models and Kolmogorov Arnold Networks

Authors: Thomas R. Harvey, Fabian Ruehle, Kit Fraser-Taliente, James Halverson

Abstract: We present a novel approach to symbolic regression using vision-capable large language models (LLMs) and the ideas behind Google DeepMind’s Funsearch. The LLM is given a plot of a univariate function and tasked with proposing an ansatz for that function. The free parameters of the ansatz are fitted using standard numerical optimisers, and a collection of such ansätze make up the population of a genetic algorithm. Unlike other symbolic regression techniques, our method does not require the specification of a set of functions to be used in regression, but with appropriate prompt engineering, we can arbitrarily condition the generative step. By using Kolmogorov Arnold Networks (KANs), we demonstrate that ``univariate is all you need’’ for symbolic regression, and extend this method to multivariate functions by learning the univariate function on each edge of a trained KAN. The combined expression is then simplified by further processing with a language model.

AC-PKAN: Attention-Enhanced and Chebyshev Polynomial-Based Physics-Informed Kolmogorov-Arnold Networks

Authors: Hangwei Zhang, Zhimu Huang, Yan Wang

Abstract: Kolmogorov-Arnold Networks (KANs) have recently shown promise for solving partial differential equations (PDEs). Yet their original formulation is computationally and memory intensive, motivating the introduction of Chebyshev Type-I-based KANs (Chebyshev1KANs). Although Chebyshev1KANs have outperformed the vanilla KANs architecture, our rigorous theoretical analysis reveals that they still suffer from rank collapse, ultimately limiting their expressive capacity. To overcome these limitations, we enhance Chebyshev1KANs by integrating wavelet-activated MLPs with learnable parameters and an internal attention mechanism. We prove that this design preserves a full-rank Jacobian and is capable of approximating solutions to PDEs of arbitrary order. Furthermore, to alleviate the loss instability and imbalance introduced by the Chebyshev polynomial basis, we externally incorporate a Residual Gradient Attention (RGA) mechanism that dynamically re-weights individual loss terms according to their gradient norms and residual magnitudes. By jointly leveraging internal and external attention, we present AC-PKAN, a novel architecture that constitutes an enhancement to weakly supervised Physics-Informed Neural Networks (PINNs) and extends the expressive power of KANs. Experimental results from nine benchmark tasks across three domains show that AC-PKAN consistently outperforms or matches state-of-the-art models such as PINNsFormer, establishing it as a highly effective tool for solving complex real-world engineering problems in zero-data or data-sparse regimes. The code will be made publicly available upon acceptance.

Personalized Control for Lower Limb Prosthesis Using Kolmogorov-Arnold Networks

Authors: SeyedMojtaba Mohasel, Alireza Afzal Aghaei, Corey Pew

Abstract: Objective: This paper investigates the potential of learnable activation functions in Kolmogorov-Arnold Networks (KANs) for personalized control in a lower-limb prosthesis. In addition, user-specific vs. pooled training data is evaluated to improve machine learning (ML) and Deep Learning (DL) performance for turn intent prediction. Method: Inertial measurement unit (IMU) data from the shank were collected from five individuals with lower-limb amputation performing turning tasks in a laboratory setting. Ability to classify an upcoming turn was evaluated for Multilayer Perceptron (MLP), Kolmogorov-Arnold Network (KAN), convolutional neural network (CNN), and fractional Kolmogorov-Arnold Networks (FKAN). The comparison of MLP and KAN (for ML models) and FKAN and CNN (for DL models) assessed the effectiveness of learnable activation functions. Models were trained separately on user-specific and pooled data to evaluate the impact of training data on their performance. Results: Learnable activation functions in KAN and FKAN did not yield significant improvement compared to MLP and CNN, respectively. Training on user-specific data yielded superior results compared to pooled data for ML models ($p < 0.05$). In contrast, no significant difference was observed between user-specific and pooled training for DL models. Significance: These findings suggest that learnable activation functions may demonstrate distinct advantages in datasets involving more complex tasks and larger volumes. In addition, pooled training showed comparable performance to user-specific training in DL models, indicating that model training for prosthesis control can utilize data from multiple participants.

Symbolic Learning of Topological Bands in Photonic Crystals

Authors: Ali Ghorashi, Sachin Vaidya, Ziming Liu, Charlotte Loh, Thomas Christensen, Max Tegmark, Marin Soljačić

Abstract: Topological photonic crystals (PhCs) that support disorder-resistant modes, protected degeneracies, and robust transport have recently been explored for applications in waveguiding, optical isolation, light trapping, and lasing. However, designing PhCs with prescribed topological properties remains challenging because of the highly nonlinear mapping from the continuous real-space design of PhCs to the discrete output space of band topology. Here, we introduce a machine learning approach to address this problem, employing Kolmogorov–Arnold networks (KANs) to predict and inversely design the band symmetries of two-dimensional PhCs with two-fold rotational (C2) symmetry. We show that a single-hidden-layer KAN, trained on a dataset of C2-symmetric unit cells, achieves high accuracy in classifying the topological classes of the lowest lying bands. We use the symbolic regression capabilities of KANs to extract algebraic formulas that express the topological classes directly in terms of the Fourier components of the dielectric function. These formulas not only retain the full predictive power of the network but also provide novel insights and enable deterministic inverse design. Using this approach, we generate photonic crystals with target topological bands, achieving high accuracy even for high-contrast, experimentally realizable structures beyond the training domain.

MedVKAN: Efficient Feature Extraction with Mamba and KAN for Medical Image Segmentation

Authors: Hancan Zhu, Jinhao Chen, Guanghua He

Abstract: Medical image segmentation has traditionally relied on convolutional neural networks (CNNs) and Transformer-based models. CNNs, however, are constrained by limited receptive fields, while Transformers face scalability challenges due to quadratic computational complexity. To over-come these issues, recent studies have explored alternative architectures. The Mamba model, a selective state-space design, achieves near-linear complexity and effectively captures long-range dependencies. Its vision-oriented variant, the Visual State Space (VSS) model, extends these strengths to image feature learning. In parallel, the Kolmogorov-Arnold Network (KAN) enhanc-es nonlinear expressiveness by replacing fixed activation functions with learnable ones. Moti-vated by these advances, we propose the VSS-Enhanced KAN (VKAN) module, which integrates VSS with the Expanded Field Convolutional KAN (EFC-KAN) as a replacement for Transformer modules, thereby strengthening feature extraction. We further embed VKAN into a U-Net frame-work, resulting in MedVKAN, an efficient medical image segmentation model. Extensive exper-iments on five public datasets demonstrate that MedVKAN achieves state-of-the-art performance on four datasets and ranks second on the remaining one. These results underscore the effective-ness of combining Mamba and KAN while introducing a novel and computationally efficient feature extraction framework. The source code is available at: https://github.com/beginner-cjh/MedVKAN.

KHRONOS: a Kernel-Based Neural Architecture for Rapid, Resource-Efficient Scientific Computation

Authors: Reza T. Batley, Sourav Saha

Abstract: Contemporary models of high dimensional physical systems are constrained by the curse of dimensionality and a reliance on dense data. We introduce KHRONOS (Kernel Expansion Hierarchy for Reduced Order, Neural Optimized Surrogates), an AI framework for model based, model free and model inversion tasks. KHRONOS constructs continuously differentiable target fields with a hierarchical composition of per-dimension kernel expansions, which are tensorized into modes and then superposed. We evaluate KHRONOS on a canonical 2D, Poisson equation benchmark: across 16 to 512 degrees of freedom (DoFs), it obtained L_2-square errors of 5e-4 down to 6e-11. This represents a greater than 100-fold gain over Kolmogorov Arnold Networks (which itself reports a 100 times improvement on MLPs/PINNs with 100 times fewer parameters) when controlling for the number of parameters. This also represents a 1e6-fold improvement in L_2-square error compared to standard linear FEM at comparable DoFs. Inference complexity is dominated by inner products, yielding sub-millisecond full-field predictions that scale to an arbitrary resolution. For inverse problems, KHRONOS facilitates rapid, iterative level set recovery in only a few forward evaluations, with sub-microsecond per sample latency. KHRONOS’s scalability, expressivity, and interpretability open new avenues in constrained edge computing, online control, computer vision, and beyond.

A Kolmogorov-Arnold Neural Model for Cascading Extremes

Authors: Miguel de Carvalho, Clemente Ferrer, Ronny Vallejos

Abstract: This paper addresses the growing concern of cascading extreme events, such as an extreme earthquake followed by a tsunami, by presenting a novel method for risk assessment focused on these domino effects. The proposed approach develops an extreme value theory framework within a Kolmogorov-Arnold network (KAN) to estimate the probability of one extreme event triggering another, conditionally on a feature vector. An extra layer is added to the KAN architecture to ensure that the parameter of interest lies within the unit interval, and we refer to the resulting neural model as KANE (KAN with Natural Enforcement). The proposed method is backed by exhaustive numerical studies and further illustrated with real-world applications to seismology and climatology.

FlashKAT: Understanding and Addressing Performance Bottlenecks in the Kolmogorov-Arnold Transformer

Authors: Matthew Raffel, Lizhong Chen

Abstract: The Kolmogorov-Arnold Network (KAN) has been gaining popularity as an alternative to the multilayer perceptron (MLP) due to its greater expressiveness and interpretability. Even so, KAN suffers from training instability and being orders of magnitude slower due to its increased computational cost, limiting its applicability to large-scale tasks. Recently, the Kolmogorov-Arnold Transformer (KAT) has been proposed, achieving FLOPs comparable to traditional Transformer models with MLPs by leveraging Group-Rational KAN (GR-KAN). Unfortunately, despite the comparable FLOPs, our testing shows that KAT remains 123x slower during training, indicating that there are other performance bottlenecks beyond FLOPs. In this paper, we conduct a series of experiments to understand the root cause of the slowdown in KAT. We uncover that the slowdown can be isolated to memory stalls, linked more specifically to inefficient gradient accumulations in the backward pass of GR-KAN. To address this memory bottleneck, we propose FlashKAT, which minimizes accesses to slow memory and the usage of atomic adds through a restructured kernel. Evaluations show that FlashKAT achieves up to an 86.5x training speedup over state-of-the-art KAT while reducing rounding errors in gradient computation.

X-KAN: Optimizing Local Kolmogorov-Arnold Networks via Evolutionary Rule-Based Machine Learning

Authors: Hiroki Shiraishi, Hisao Ishibuchi, Masaya Nakata

Abstract: Function approximation is a critical task in various fields. However, existing neural network approaches struggle with locally complex or discontinuous functions due to their reliance on a single global model covering the entire problem space. We propose X-KAN, a novel method that optimizes multiple local Kolmogorov-Arnold Networks (KANs) through an evolutionary rule-based machine learning framework called XCSF. X-KAN combines KAN’s high expressiveness with XCSF’s adaptive partitioning capability by implementing local KAN models as rule consequents and defining local regions via rule antecedents. Our experimental results on artificial test functions and real-world datasets demonstrate that X-KAN significantly outperforms conventional methods, including XCSF, Multi-Layer Perceptron, and KAN, in terms of approximation accuracy. Notably, X-KAN effectively handles functions with locally complex or discontinuous structures that are challenging for conventional KAN, using a compact set of rules (average 7.2 $\pm$ 2.3 rules). These results validate the effectiveness of using KAN as a local model in XCSF, which evaluates the rule fitness based on both accuracy and generality. Our X-KAN implementation is available at https://github.com/YNU-NakataLab/X-KAN.

Interpretable Reinforcement Learning for Load Balancing using Kolmogorov-Arnold Networks

Authors: Kamal Singh, Sami Marouani, Ahmad Al Sheikh, Pham Tran Anh Quang, Amaury Habrard

Abstract: Reinforcement learning (RL) has been increasingly applied to network control problems, such as load balancing. However, existing RL approaches often suffer from lack of interpretability and difficulty in extracting controller equations. In this paper, we propose the use of Kolmogorov-Arnold Networks (KAN) for interpretable RL in network control. We employ a PPO agent with a 1-layer actor KAN model and an MLP Critic network to learn load balancing policies that maximise throughput utility, minimize loss as well as delay. Our approach allows us to extract controller equations from the learned neural networks, providing insights into the decision-making process. We evaluate our approach using different reward functions demonstrating its effectiveness in improving network performance while providing interpretable policies.

Khan-GCL: Kolmogorov-Arnold Network Based Graph Contrastive Learning with Hard Negatives

Authors: Zihu Wang, Boxun Xu, Hejia Geng, Peng Li

Abstract: Graph contrastive learning (GCL) has demonstrated great promise for learning generalizable graph representations from unlabeled data. However, conventional GCL approaches face two critical limitations: (1) the restricted expressive capacity of multilayer perceptron (MLP) based encoders, and (2) suboptimal negative samples that either from random augmentations-failing to provide effective ‘hard negatives’-or generated hard negatives without addressing the semantic distinctions crucial for discriminating graph data. To this end, we propose Khan-GCL, a novel framework that integrates the Kolmogorov-Arnold Network (KAN) into the GCL encoder architecture, substantially enhancing its representational capacity. Furthermore, we exploit the rich information embedded within KAN coefficient parameters to develop two novel critical feature identification techniques that enable the generation of semantically meaningful hard negative samples for each graph representation. These strategically constructed hard negatives guide the encoder to learn more discriminative features by emphasizing critical semantic differences between graphs. Extensive experiments demonstrate that our approach achieves state-of-the-art performance compared to existing GCL methods across a variety of datasets and tasks.

Degree-Optimized Cumulative Polynomial Kolmogorov-Arnold Networks

Authors: Mathew Vanherreweghe, Lirandë Pira, Patrick Rebentrost

Abstract: We introduce cumulative polynomial Kolmogorov-Arnold networks (CP-KAN), a neural architecture combining Chebyshev polynomial basis functions and quadratic unconstrained binary optimization (QUBO). Our primary contribution involves reformulating the degree selection problem as a QUBO task, reducing the complexity from $O(D^N)$ to a single optimization step per layer. This approach enables efficient degree selection across neurons while maintaining computational tractability. The architecture performs well in regression tasks with limited data, showing good robustness to input scales and natural regularization properties from its polynomial basis. Additionally, theoretical analysis establishes connections between CP-KAN’s performance and properties of financial time series. Our empirical validation across multiple domains demonstrates competitive performance compared to several traditional architectures tested, especially in scenarios where data efficiency and numerical stability are important. Our implementation, including strategies for managing computational overhead in larger networks is available in Ref.~\citep{cpkan_implementation}.

Leveraging KANs for Expedient Training of Multichannel MLPs via Preconditioning and Geometric Refinement

Authors: Jonas A. Actor, Graham Harper, Ben Southworth, Eric C. Cyr

Abstract: Multilayer perceptrons (MLPs) are a workhorse machine learning architecture, used in a variety of modern deep learning frameworks. However, recently Kolmogorov-Arnold Networks (KANs) have become increasingly popular due to their success on a range of problems, particularly for scientific machine learning tasks. In this paper, we exploit the relationship between KANs and multichannel MLPs to gain structural insight into how to train MLPs faster. We demonstrate the KAN basis (1) provides geometric localized support, and (2) acts as a preconditioned descent in the ReLU basis, overall resulting in expedited training and improved accuracy. Our results show the equivalence between free-knot spline KAN architectures, and a class of MLPs that are refined geometrically along the channel dimension of each weight tensor. We exploit this structural equivalence to define a hierarchical refinement scheme that dramatically accelerates training of the multi-channel MLP architecture. We show further accuracy improvements can be had by allowing the $1$D locations of the spline knots to be trained simultaneously with the weights. These advances are demonstrated on a range of benchmark examples for regression and scientific machine learning.

COLORA: Efficient Fine-Tuning for Convolutional Models with a Study Case on Optical Coherence Tomography Image Classification

Authors: Mariano Rivera, Angello Hoyos

Abstract: We introduce CoLoRA (Convolutional Low-Rank Adaptation), a parameter-efficient fine-tuning method for convolutional neural networks (CNNs). CoLoRA extends LoRA to convolutional layers by decomposing kernel updates into lightweight depthwise and pointwise components.This design reduces the number of trainable parameters to 0.2 compared to conventional fine-tuning, preserves the original model size, and allows merging updates into the pretrained weights after each epoch, keeping inference complexity unchanged. On OCTMNISTv2, CoLoRA applied to VGG16 and ResNet50 achieves up to 1 percent accuracy and 0.013 AUC improvements over strong baselines (Vision Transformers, state-space, and Kolmogorov Arnold models) while reducing per-epoch training time by nearly 20 percent. Results indicate that CoLoRA provides a stable and effective alternative to full fine-tuning for medical image classification.

TK-Mamba: Marrying KAN With Mamba for Text-Driven 3D Medical Image Segmentation

Authors: Haoyu Yang, Yutong Guan, Meixing Shi, Yuxiang Cai, Jintao Chen, Sun Bing, Wenhui Lei, Mianxin Liu, Xiaoming Shi, Yankai Jiang, Jianwei Yin

Abstract: 3D medical image segmentation is important for clinical diagnosis and treatment but faces challenges from high-dimensional data and complex spatial dependencies. Traditional single-modality networks, such as CNNs and Transformers, are often limited by computational inefficiency and constrained contextual modeling in 3D settings. To alleviate these limitations, we propose TK-Mamba, a multimodal framework that fuses the linear-time Mamba with Kolmogorov-Arnold Networks (KAN) to form an efficient hybrid backbone. Our approach is characterized by two primary technical contributions. Firstly, we introduce the novel 3D-Group-Rational KAN (3D-GR-KAN), which marks the first application of KAN in 3D medical imaging, providing a superior and computationally efficient nonlinear feature transformation crucial for complex volumetric structures. Secondly, we devise a dual-branch text-driven strategy using Pubmedclip’s embeddings. This strategy significantly enhances segmentation robustness and accuracy by simultaneously capturing inter-organ semantic relationships to mitigate label inconsistencies and aligning image features with anatomical texts. By combining this advanced backbone and vision-language knowledge, TK-Mamba offers a unified and scalable solution for both multi-organ and tumor segmentation. Experiments on multiple datasets demonstrate that our framework achieves state-of-the-art performance in both organ and tumor segmentation tasks, surpassing existing methods in both accuracy and efficiency. Our code is publicly available at https://github.com/yhy-whu/TK-Mamba

Kolmogorov-Arnold Networks for Turbulence Anisotropy Mapping

Authors: Nikhila Kalia, Ryley McConkey, Eugene Yee, Fue-Sang Lien

Abstract: This study evaluates the generalization performance and representation efficiency (parsimony) of a previously introduced Tensor Basis Kolmogorov-Arnold Network (TBKAN) architecture for data-driven turbulence modeling. The TBKAN framework replaces the multi-layer perceptron (MLP) used in either the standard or modified Tensor Basis Neural Network (TBNN) with a Kolmogorov-Arnold network (KAN), which significantly reduces the model complexity while providing a structure that potentially can be used with symbolic regression to provide a physical interpretability that is not available in a ‘black box’ MLP. While some prior work demonstrated TBKAN’s feasibility for modeling a ‘simple’ flat plate boundary layer flow, this study extends the TBKAN architecture to model more complex benchmark flows, in particular, square duct and periodic hills flows which exhibit strong turbulence anisotropy, secondary motion, and flow separation and reattachment. A realizability-informed loss function is employed to constrain the model predictions, and, for the first time, TBKAN predictions are stably injected into the Reynolds-averaged Navier-Stokes equations to provide it a posteriori predictions of the mean velocity field.

“KAN you hear me?” Exploring Kolmogorov-Arnold Networks for Spoken Language Understanding

Authors: Alkis Koudounas, Moreno La Quatra, Eliana Pastor, Sabato Marco Siniscalchi, Elena Baralis

Abstract: Kolmogorov-Arnold Networks (KANs) have recently emerged as a promising alternative to traditional neural architectures, yet their application to speech processing remains under explored. This work presents the first investigation of KANs for Spoken Language Understanding (SLU) tasks. We experiment with 2D-CNN models on two datasets, integrating KAN layers in five different configurations within the dense block. The best-performing setup, which places a KAN layer between two linear layers, is directly applied to transformer-based models and evaluated on five SLU datasets with increasing complexity. Our results show that KAN layers can effectively replace the linear layers, achieving comparable or superior performance in most cases. Finally, we provide insights into how KAN and linear layers on top of transformers differently attend to input regions of the raw waveforms.

FMEnets: Flow, Material, and Energy networks for non-ideal plug flow reactor design

Authors: Chenxi Wu, Juan Diego Toscano, Khemraj Shukla, Yingjie Chen, Ali Shahmohammadi, Edward Raymond, Thomas Toupy, Neda Nazemifard, Charles Papageorgiou, George Em Karniadakis

Abstract: We propose FMEnets, a physics-informed machine learning framework for the design and analysis of non-ideal plug flow reactors. FMEnets integrates the fundamental governing equations (Navier-Stokes for fluid flow, material balance for reactive species transport, and energy balance for temperature distribution) into a unified multi-scale network model. The framework is composed of three interconnected sub-networks with independent optimizers that enable both forward and inverse problem-solving. In the forward mode, FMEnets predicts velocity, pressure, species concentrations, and temperature profiles using only inlet and outlet information. In the inverse mode, FMEnets utilizes sparse multi-residence-time measurements to simultaneously infer unknown kinetic parameters and states. FMEnets can be implemented either as FME-PINNs, which employ conventional multilayer perceptrons, or as FME-KANs, based on Kolmogorov-Arnold Networks. Comprehensive ablation studies highlight the critical role of the FMEnets architecture in achieving accurate predictions. Specifically, FME-KANs are more robust to noise than FME-PINNs, although both representations are comparable in accuracy and speed in noise-free conditions. The proposed framework is applied to three different sets of reaction scenarios and is compared with finite element simulations. FMEnets effectively captures the complex interactions, achieving relative errors less than 2.5% for the unknown kinetic parameters. The new network framework not only provides a computationally efficient alternative for reactor design and optimization, but also opens new avenues for integrating empirical correlations, limited and noisy experimental data, and fundamental physical equations to guide reactor design.

Input Convex Kolmogorov Arnold Networks

Authors: Thomas Deschatre, Xavier Warin

Citation Count: 1

Abstract: This article presents an input convex neural network architecture using Kolmogorov-Arnold networks (ICKAN). Two specific networks are presented: the first is based on a low-order, linear-by-part, representation of functions, and a universal approximation theorem is provided. The second is based on cubic splines, for which only numerical results support convergence. We demonstrate on simple tests that these networks perform competitively with classical input convex neural networks (ICNNs). In a second part, we use the networks to solve some optimal transport problems needing a convex approximation of functions and demonstrate their effectiveness. Comparisons with ICNNs show that cubic ICKANs produce results similar to those of classical ICNNs.

Taylor expansion-based Kolmogorov-Arnold network for blind image quality assessment

Authors: Ze Chen, Shaode Yu

Abstract: Kolmogorov-Arnold Network (KAN) has attracted growing interest for its strong function approximation capability. In our previous work, KAN and its variants were explored in score regression for blind image quality assessment (BIQA). However, these models encounter challenges when processing high-dimensional features, leading to limited performance gains and increased computational cost. To address these issues, we propose TaylorKAN that leverages the Taylor expansions as learnable activation functions to enhance local approximation capability. To improve the computational efficiency, network depth reduction and feature dimensionality compression are integrated into the TaylorKAN-based score regression pipeline. On five databases (BID, CLIVE, KonIQ, SPAQ, and FLIVE) with authentic distortions, extensive experiments demonstrate that TaylorKAN consistently outperforms the other KAN-related models, indicating that the local approximation via Taylor expansions is more effective than global approximation using orthogonal functions. Its generalization capacity is validated through inter-database experiments. The findings highlight the potential of TaylorKAN as an efficient and robust model for high-dimensional score regression.

Localized Weather Prediction Using Kolmogorov-Arnold Network-Based Models and Deep RNNs

Authors: Ange-Clement Akazan, Verlon Roel Mbingui, Gnankan Landry Regis N’guessan, Issa Karambal

Abstract: Weather forecasting is crucial for managing risks and economic planning, particularly in tropical Africa, where extreme events severely impact livelihoods. Yet, existing forecasting methods often struggle with the region’s complex, non-linear weather patterns. This study benchmarks deep recurrent neural networks such as $\texttt{LSTM, GRU, BiLSTM, BiGRU}$, and Kolmogorov-Arnold-based models $(\texttt{KAN} and \texttt{TKAN})$ for daily forecasting of temperature, precipitation, and pressure in two tropical cities: Abidjan, Cote d’Ivoire (Ivory Coast) and Kigali (Rwanda). We further introduce two customized variants of $ \texttt{TKAN}$ that replace its original $\texttt{SiLU}$ activation function with $ \texttt{GeLU}$ and \texttt{MiSH}, respectively. Using station-level meteorological data spanning from 2010 to 2024, we evaluate all the models on standard regression metrics. $\texttt{KAN}$ achieves temperature prediction ($R^2=0.9986$ in Abidjan, $0.9998$ in Kigali, $\texttt{MSE} < 0.0014~^\circ C ^2$), while $\texttt{TKAN}$ variants minimize absolute errors for precipitation forecasting in low-rainfall regimes. The customized $\texttt{TKAN}$ models demonstrate improvements over the standard $\texttt{TKAN}$ across both datasets. Classical \texttt{RNNs} remain highly competitive for atmospheric pressure ($R^2 \approx 0.83{-}0.86$), outperforming $\texttt{KAN}$-based models in this task. These results highlight the potential of spline-based neural architectures for efficient and data-efficient forecasting.

Automated Modeling Method for Pathloss Model Discovery

Authors: Ahmad Anaqreh, Shih-Kai Chou, Blaž Bertalanič, Mihael Mohorčič, Thomas Lagkas, Carolina Fortuna

Abstract: Modeling propagation is the cornerstone for designing and optimizing next-generation wireless systems, with a particular emphasis on 5G and beyond era. Traditional modeling methods have long relied on statistic-based techniques to characterize propagation behavior across different environments. With the expansion of wireless communication systems, there is a growing demand for methods that guarantee the accuracy and interpretability of modeling. Artificial intelligence (AI)-based techniques, in particular, are increasingly being adopted to overcome this challenge, although the interpretability is not assured with most of these methods. Inspired by recent advancements in AI, this paper proposes a novel approach that accelerates the discovery of path loss models while maintaining interpretability. The proposed method automates the formulation, evaluation, and refinement of the model, facilitating the discovery of the model. We examine two techniques: one based on Deep Symbolic Regression, offering full interpretability, and the second based on Kolmogorov-Arnold Networks, providing two levels of interpretability. Both approaches are evaluated on two synthetic and two real-world datasets. Our results show that Kolmogorov-Arnold Networks achieve the coefficient of determination value R^2 close to 1 with minimal prediction error, while Deep Symbolic Regression generates compact models with moderate accuracy. Moreover, on the selected examples, we demonstrate that automated methods outperform traditional methods, achieving up to 75% reduction in prediction errors, offering accurate and explainable solutions with potential to increase the efficiency of discovering next-generation path loss models.

SPPSFormer: High-quality Superpoint-based Transformer for Roof Plane Instance Segmentation from Point Clouds

Authors: Cheng Zeng, Xiatian Qi, Chi Chen, Kai Sun, Wangle Zhang, Yuxuan Liu, Yan Meng, Bisheng Yang

Abstract: Transformers have been seldom employed in point cloud roof plane instance segmentation, which is the focus of this study, and existing superpoint Transformers suffer from limited performance due to the use of low-quality superpoints. To address this challenge, we establish two criteria that high-quality superpoints for Transformers should satisfy and introduce a corresponding two-stage superpoint generation process. The superpoints generated by our method not only have accurate boundaries, but also exhibit consistent geometric sizes and shapes, both of which greatly benefit the feature learning of superpoint Transformers. To compensate for the limitations of deep learning features when the training set size is limited, we incorporate multidimensional handcrafted features into the model. Additionally, we design a decoder that combines a Kolmogorov-Arnold Network with a Transformer module to improve instance prediction and mask extraction. Finally, our network’s predictions are refined using traditional algorithm-based postprocessing. For evaluation, we annotated a real-world dataset and corrected annotation errors in the existing RoofN3D dataset. Experimental results show that our method achieves state-of-the-art performance on our dataset, as well as both the original and reannotated RoofN3D datasets. Moreover, our model is not sensitive to plane boundary annotations during training, significantly reducing the annotation burden. Through comprehensive experiments, we also identified key factors influencing roof plane segmentation performance: in addition to roof types, variations in point cloud density, density uniformity, and 3D point precision have a considerable impact. These findings underscore the importance of incorporating data augmentation strategies that account for point cloud quality to enhance model robustness under diverse and challenging conditions.

How can AI reduce fall injuries in the workplace?

Authors: Nicholas Cartocci, Antonios E. Gkikakis, Roberto F. Pitzalis, Fabio Pera, Maria Teresa Settino, Darwin G. Caldwell, Jesús Ortiz

Abstract: Fall-caused injuries are common in all types of work environments, including offices. They are the main cause of absences longer than three days, especially for small and medium-sized businesses (SMEs). However, data, data amount, data heterogeneity, and stringent processing time constraints continue to pose challenges to real-time fall detection. This work proposes a new approach based on a recurrent neural network (RNN) for Fall Detection and a Kolmogorov-Arnold Network (KAN) to estimate the time of impact of the fall. The approach is tested on SisFall, a dataset consisting of 2706 Activities of Daily Living (ADLs) and 1798 falls recorded by three sensors. The results show that the proposed approach achieves an average TPR of 82.6% and TNR of 98.4% for fall sequences and 94.4% in ADL. Besides, the Root Mean Squared Error of the estimated time of impact is approximately 160ms.

June

Probing Quantum Spin Systems with Kolmogorov-Arnold Neural Network Quantum States

Authors: Mahmud Ashraf Shamim, Eric A F Reinhardt, Talal Ahmed Chowdhury, Sergei Gleyzer, Paulo T Araujo

Abstract: Neural Quantum States (NQS) are a class of variational wave functions parametrized by neural networks (NNs) to study quantum many-body systems. In this work, we propose \texttt{SineKAN}, a NQS \textit{ansatz} based on Kolmogorov-Arnold Networks (KANs), to represent quantum mechanical wave functions as nested univariate functions. We show that \texttt{SineKAN} wavefunction with learnable sinusoidal activation functions can capture the ground state energies, fidelities and various correlation functions of the one dimensional Transverse-Field Ising model, Anisotropic Heisenberg model, and Antiferromagnetic $J_{1}-J_{2}$ model with different chain lengths. In our study of the $J_1-J_2$ model with $L=100$ sites, we find that the \texttt{SineKAN} model outperforms several previously explored neural quantum state \textit{ansätze}, including Restricted Boltzmann Machines (RBMs), Long Short-Term Memory models (LSTMs), and Multi-layer Perceptrons (MLP) \textit{a.k.a.} Feed Forward Neural Networks, when compared to the results obtained from the Density Matrix Renormalization Group (DMRG) algorithm. We find that \texttt{SineKAN} models can be trained to high precisions and accuracies with minimal computational costs.

Kolmogorov-Arnold Wavefunctions

Authors: Paulo F. Bedaque, Jacob Cigliano, Hersh Kumar, Srijit Paul, Suryansh Rajawat

Abstract: This work investigates Kolmogorov-Arnold network-based wavefunction ansatz as viable representations for quantum Monte Carlo simulations. Through systematic analysis of one-dimensional model systems, we evaluate their computational efficiency and representational power against established methods. Our numerical experiments suggest some efficient training methods and we explore how the computational cost scales with desired precision, particle number, and system parameters. Roughly speaking, KANs seem to be 10 times cheaper computationally than other neural network based ansatz. We also introduce a novel approach for handling strong short-range potentials-a persistent challenge for many numerical techniques-which generalizes efficiently to higher-dimensional, physically relevant systems with short-ranged strong potentials common in atomic and nuclear physics.

Multi-Exit Kolmogorov-Arnold Networks: enhancing accuracy and parsimony

Authors: James Bagrow, Josh Bongard

Abstract: Kolmogorov-Arnold Networks (KANs) uniquely combine high accuracy with interpretability, making them valuable for scientific modeling. However, it is unclear a priori how deep a network needs to be for any given task, and deeper KANs can be difficult to optimize and interpret. Here we introduce multi-exit KANs, where each layer includes its own prediction branch, enabling the network to make accurate predictions at multiple depths simultaneously. This architecture provides deep supervision that improves training while discovering the right level of model complexity for each task. Multi-exit KANs consistently outperform standard, single-exit versions on synthetic functions, dynamical systems, and real-world datasets. Remarkably, the best predictions often come from earlier, simpler exits, revealing that these networks naturally identify smaller, more parsimonious and interpretable models without sacrificing accuracy. To automate this discovery, we develop a differentiable “learning-to-exit” algorithm that balances contributions from exits during training. Our approach offers scientists a practical way to achieve both high performance and interpretability, addressing a fundamental challenge in machine learning for scientific discovery.

Dynamic Graph CNN with Jacobi Kolmogorov-Arnold Networks for 3D Classification of Point Sets

Authors: Hanaa El Afia, Said Ohamouddou, Raddouane Chiheb, Abdellatif El Afia

Abstract: We introduce Jacobi-KAN-DGCNN, a framework that integrates Dynamic Graph Convolutional Neural Network (DGCNN) with Jacobi Kolmogorov-Arnold Networks (KAN) for the classification of three-dimensional point clouds. This method replaces Multi-Layer Perceptron (MLP) layers with adaptable univariate polynomial expansions within a streamlined DGCNN architecture, circumventing deep levels for both MLP and KAN to facilitate a layer-by-layer comparison. In comparative experiments on the ModelNet40 dataset, KAN layers employing Jacobi polynomials outperform the traditional linear layer-based DGCNN baseline in terms of accuracy and convergence speed, while maintaining parameter efficiency. Our results demonstrate that higher polynomial degrees do not automatically improve performance, highlighting the need for further theoretical and empirical investigation to fully understand the interactions between polynomial bases, degrees, and the mechanisms of graph-based learning.

Improving Memory Efficiency for Training KANs via Meta Learning

Authors: Zhangchi Zhao, Jun Shu, Deyu Meng, Zongben Xu

Abstract: Inspired by the Kolmogorov-Arnold representation theorem, KANs offer a novel framework for function approximation by replacing traditional neural network weights with learnable univariate functions. This design demonstrates significant potential as an efficient and interpretable alternative to traditional MLPs. However, KANs are characterized by a substantially larger number of trainable parameters, leading to challenges in memory efficiency and higher training costs compared to MLPs. To address this limitation, we propose to generate weights for KANs via a smaller meta-learner, called MetaKANs. By training KANs and MetaKANs in an end-to-end differentiable manner, MetaKANs achieve comparable or even superior performance while significantly reducing the number of trainable parameters and maintaining promising interpretability. Extensive experiments on diverse benchmark tasks, including symbolic regression, partial differential equation solving, and image classification, demonstrate the effectiveness of MetaKANs in improving parameter efficiency and memory usage. The proposed method provides an alternative technique for training KANs, that allows for greater scalability and extensibility, and narrows the training cost gap with MLPs stated in the original paper of KANs. Our code is available at https://github.com/Murphyzc/MetaKAN.

Neural Tangent Kernel Analysis to Probe Convergence in Physics-informed Neural Solvers: PIKANs vs. PINNs

Authors: Salah A. Faroughi, Farinaz Mostajeran

Abstract: Physics-informed Kolmogorov-Arnold Networks (PIKANs), and in particular their Chebyshev-based variants (cPIKANs), have recently emerged as promising models for solving partial differential equations (PDEs). However, their training dynamics and convergence behavior remain largely unexplored both theoretically and numerically. In this work, we aim to advance the theoretical understanding of cPIKANs by analyzing them using Neural Tangent Kernel (NTK) theory. Our objective is to discern the evolution of kernel structure throughout gradient-based training and its subsequent impact on learning efficiency. We first derive the NTK of standard cKANs in a supervised setting, and then extend the analysis to the physics-informed context. We analyze the spectral properties of NTK matrices, specifically their eigenvalue distributions and spectral bias, for four representative PDEs: the steady-state Helmholtz equation, transient diffusion and Allen-Cahn equations, and forced vibrations governed by the Euler-Bernoulli beam equation. We also conduct an investigation into the impact of various optimization strategies, e.g., first-order, second-order, and hybrid approaches, on the evolution of the NTK and the resulting learning dynamics. Results indicate a tractable behavior for NTK in the context of cPIKANs, which exposes learning dynamics that standard physics-informed neural networks (PINNs) cannot capture. Spectral trends also reveal when domain decomposition improves training, directly linking kernel behavior to convergence rates under different setups. To the best of our knowledge, this is the first systematic NTK study of cPIKANs, providing theoretical insight that clarifies and predicts their empirical performance.

System Identification Using Kolmogorov-Arnold Networks: A Case Study on Buck Converters

Authors: Nart Gashi, Panagiotis Kakosimos, George Papafotiou

Abstract: Kolmogorov-Arnold Networks (KANs) are emerging as a powerful framework for interpretable and efficient system identification in dynamic systems. By leveraging the Kolmogorov-Arnold representation theorem, KANs enable function approximation through learnable activation functions, offering improved scalability, accuracy, and interpretability compared to traditional neural networks. This paper investigates the application of KANs to model and analyze the dynamics of a buck converter system, focusing on state-space parameter estimation along with discovering the system equations. Using simulation data, the methodology involves approximating state derivatives with KANs, constructing interpretable state-space representations, and validating these models through numerical experiments. The results demonstrate the ability of KANs to accurately identify system dynamics, verify model consistency, and detect parameter changes, providing valuable insights into their applicability for system identification in modern industrial systems.

TFKAN: Time-Frequency KAN for Long-Term Time Series Forecasting

Authors: Xiaoyan Kui, Canwei Liu, Qinsong Li, Zhipeng Hu, Yangyang Shi, Weixin Si, Beiji Zou

Abstract: Kolmogorov-Arnold Networks (KANs) are highly effective in long-term time series forecasting due to their ability to efficiently represent nonlinear relationships and exhibit local plasticity. However, prior research on KANs has predominantly focused on the time domain, neglecting the potential of the frequency domain. The frequency domain of time series data reveals recurring patterns and periodic behaviors, which complement the temporal information captured in the time domain. To address this gap, we explore the application of KANs in the frequency domain for long-term time series forecasting. By leveraging KANs’ adaptive activation functions and their comprehensive representation of signals in the frequency domain, we can more effectively learn global dependencies and periodic patterns. To integrate information from both time and frequency domains, we propose the $\textbf{T}$ime-$\textbf{F}$requency KAN (TFKAN). TFKAN employs a dual-branch architecture that independently processes features from each domain, ensuring that the distinct characteristics of each domain are fully utilized without interference. Additionally, to account for the heterogeneity between domains, we introduce a dimension-adjustment strategy that selectively upscales only in the frequency domain, enhancing efficiency while capturing richer frequency information. Experimental results demonstrate that TFKAN consistently outperforms state-of-the-art (SOTA) methods across multiple datasets. The code is available at https://github.com/LcWave/TFKAN.

Rethinking Distributional IVs: KAN-Powered D-IV-LATE & Model Choice

Author: Charles Shaw

Abstract: The double/debiased machine learning (DML) framework has become a cornerstone of modern causal inference, allowing researchers to utilise flexible machine learning models for the estimation of nuisance functions without introducing first-order bias into the final parameter estimate. However, the choice of machine learning model for the nuisance functions is often treated as a minor implementation detail. In this paper, we argue that this choice can have a profound impact on the substantive conclusions of the analysis. We demonstrate this by presenting and comparing two distinct Distributional Instrumental Variable Local Average Treatment Effect (D-IV-LATE) estimators. The first estimator leverages standard machine learning models like Random Forests for nuisance function estimation, while the second is a novel estimator employing Kolmogorov-Arnold Networks (KANs). We establish the asymptotic properties of these estimators and evaluate their performance through Monte Carlo simulations. An empirical application analysing the distributional effects of 401(k) participation on net financial assets reveals that the choice of machine learning model for nuisance functions can significantly alter substantive conclusions, with the KAN-based estimator suggesting more complex treatment effect heterogeneity. These findings underscore a critical “caveat emptor”. The selection of nuisance function estimators is not a mere implementation detail. Instead, it is a pivotal choice that can profoundly impact research outcomes in causal inference.

The effect of Quantum Time Crystal Computing to Quantum Machine Learning methods

Authors: Hikaru Wakaura, Andriyan B. Suksmono

Abstract: Many body localization shows the robustness for external perturbations and time reversal symmetry on Time Crystal. This Time Crystal prolongs the coherence time, hence, it is used for quantum computers as qubits. Therefore, we established the method to exploit Time Crystals for quantum computing by controlling external noise called Quantum Time Crystal Computing and demonstrated solving the problem of generating correct waves using Quantum Reservoir Computing, and fitting of given function using Quantum Neural Network and Variational Quantum Kolmogorov-Arnold Network. As a consequence, we revealed that Quantum Time Crystal Computing lower the accuracy of Quantum Reservoir Computing and improved the accuracy of Quantum Neural Network and Variational Quantum Kolmogorov-Arnold Network. This result may be the one of milestones of Quantum Error Mitigation as the case that noise improves the accuracy of Quantum Machine Learning.

Kolmogorov-Arnold Network for Gene Regulatory Network Inference

Authors: Tsz Pan Tong, Aoran Wang, George Panagopoulos, Jun Pang

Abstract: Gene regulation is central to understanding cellular processes and development, potentially leading to the discovery of new treatments for diseases and personalized medicine. Inferring gene regulatory networks (GRNs) from single-cell RNA sequencing (scRNA-seq) data presents significant challenges due to its high dimensionality and complexity. Existing tree-based models, such as GENIE3 and GRNBOOST2, demonstrated scalability and explainability in GRN inference, but they cannot distinguish regulation types nor effectively capture continuous cellular dynamics. In this paper, we introduce scKAN, a novel model that employs a Kolmogorov-Arnold network (KAN) with explainable AI to infer GRNs from scRNA-seq data. By modeling gene expression as differentiable functions matching the smooth nature of cellular dynamics, scKAN can accurately and precisely detect activation and inhibition regulations through explainable AI and geometric tools. We conducted extensive experiments on the BEELINE benchmark, and scKAN surpasses and improves the leading signed GRN inference models ranging from 5.40\% to 28.37\% in AUROC and from 1.97\% to 40.45\% in AUPRC. These results highlight the potential of scKAN in capturing the underlying biological processes in gene regulation without prior knowledge of the graph structure.

Scientifically-Interpretable Reasoning Network (ScIReN): Discovering Hidden Relationships in the Carbon Cycle and Beyond

Authors: Joshua Fan, Haodi Xu, Feng Tao, Md Nasim, Marc Grimson, Yiqi Luo, Carla P. Gomes

Abstract: Soils have potential to mitigate climate change by sequestering carbon from the atmosphere, but the soil carbon cycle remains poorly understood. Scientists have developed process-based models of the soil carbon cycle based on existing knowledge, but they contain numerous unknown parameters and often fit observations poorly. On the other hand, neural networks can learn patterns from data, but do not respect known scientific laws, and are too opaque to reveal novel scientific relationships. We thus propose Scientifically-Interpretable Reasoning Network (ScIReN), a fully-transparent framework that combines interpretable neural and process-based reasoning. An interpretable encoder predicts scientifically-meaningful latent parameters, which are then passed through a differentiable process-based decoder to predict labeled output variables. While the process-based decoder enforces existing scientific knowledge, the encoder leverages Kolmogorov-Arnold networks (KANs) to reveal interpretable relationships between input features and latent parameters, using novel smoothness penalties to balance expressivity and simplicity. ScIReN also introduces a novel hard-sigmoid constraint layer to restrict latent parameters into prior ranges while maintaining interpretability. We apply ScIReN on two tasks: simulating the flow of organic carbon through soils, and modeling ecosystem respiration from plants. On both tasks, ScIReN outperforms or matches black-box models in predictive accuracy, while greatly improving scientific interpretability – it can infer latent scientific mechanisms and their relationships with input features.

Pushing the Performance of Synthetic Speech Detection with Kolmogorov-Arnold Networks and Self-Supervised Learning Models

Authors: Tuan Dat Phuong, Long-Vu Hoang, Huy Dat Tran

Abstract: Recent advancements in speech synthesis technologies have led to increasingly advanced spoofing attacks, posing significant challenges for automatic speaker verification systems. While systems based on self-supervised learning (SSL) models, particularly the XLSR-Conformer model, have demonstrated remarkable performance in synthetic speech detection, there remains room for architectural improvements. In this paper, we propose a novel approach that replaces the traditional Multi-Layer Perceptron in the XLSR-Conformer model with a Kolmogorov-Arnold Network (KAN), a novel architecture based on the Kolmogorov-Arnold representation theorem. Our results on ASVspoof2021 demonstrate that integrating KAN into the SSL-based models can improve the performance by 60.55% relatively on LA and DF sets, further achieving 0.70% EER on the 21LA set. These findings suggest that incorporating KAN into SSL-based models is a promising direction for advances in synthetic speech detection.

ss-Mamba: Semantic-Spline Selective State-Space Model

Author: Zuochen Ye

Abstract: We propose ss-Mamba, a novel foundation model that enhances time series forecasting by integrating semantic-aware embeddings and adaptive spline-based temporal encoding within a selective state-space modeling framework. Building upon the recent success of Transformer architectures, ss-Mamba adopts the Mamba selective state space model as an efficient alternative that achieves comparable performance while significantly reducing computational complexity from quadratic to linear time. Semantic index embeddings, initialized from pretrained language models, allow effective generalization to previously unseen series through meaningful semantic priors. Additionally, spline-based Kolmogorov-Arnold Networks (KAN) dynamically and interpretably capture complex seasonalities and non-stationary temporal effects, providing a powerful enhancement over conventional temporal feature encodings. Extensive experimental evaluations confirm that ss-Mamba delivers superior accuracy, robustness, and interpretability, demonstrating its capability as a versatile and computationally efficient alternative to traditional Transformer-based models in time-series forecasting.

HiPreNets: High-Precision Neural Networks through Progressive Training

Authors: Ethan Mulle, Wei Kang, Qi Gong

Abstract: Deep neural networks are powerful tools for solving nonlinear problems in science and engineering, but training highly accurate models becomes challenging as problem complexity increases. Non-convex optimization and sensitivity to hyperparameters make consistent performance improvement difficult, and traditional approaches prioritize minimizing mean squared error while overlooking the $L^{\infty}$ norm error that is critical in safety-sensitive applications. To address these challenges, we present HiPreNets, a progressive framework for training high-precision neural networks through sequential residual refinements. Starting from an initial network, each stage trains a refinement network on the normalized residuals of the ensemble so far, systematically reducing both average and worst-case error. A key theme throughout the framework is concentrating training effort on high-error regions of the input domain, which we pursue through complementary techniques including loss function design, adaptive data sampling, localized patching, and boundary-aware training. We validate the framework on benchmark regression problems from the Feynman dataset, where it consistently outperforms standard fully connected networks and reported Kolmogorov-Arnold Networks results, with accuracy approaching machine precision depending on select problems. We further apply the framework to learning the flow map of a 20-dimensional power system ODE, which appears to be the highest dimensional problem studied using this class of multistage methods, achieving substantial reductions in both RMSE and $L^{\infty}$ norm error while enabling a surrogate that predicts system state $238\times$ faster than direct numerical simulation.

State-Space Kolmogorov Arnold Networks for Interpretable Nonlinear System Identification

Authors: Gonçalo Granjal Cruz, Balazs Renczes, Mark C Runacres, Jan Decuyper

Abstract: While accurate, black-box system identification models lack interpretability of the underlying system dynamics. This paper proposes State-Space Kolmogorov-Arnold Networks (SS-KAN) to address this challenge by integrating Kolmogorov-Arnold Networks within a state-space framework. The proposed model is validated on two benchmark systems: the Silverbox and the Wiener-Hammerstein benchmarks. Results show that SS-KAN provides enhanced interpretability due to sparsity-promoting regularization and the direct visualization of its learned univariate functions, which reveal system nonlinearities at the cost of accuracy when compared to state-of-the-art black-box models, highlighting SS-KAN as a promising approach for interpretable nonlinear system identification, balancing accuracy and interpretability of nonlinear system dynamics.

Structured Kolmogorov-Arnold Neural ODEs for Interpretable Learning and Symbolic Discovery of Nonlinear Dynamics

Authors: Wei Liu, Kiran Bacsa, Loon Ching Tang, Eleni Chatzi

Abstract: Understanding and modeling nonlinear dynamical systems is a fundamental challenge across science and engineering. Deep learning has shown remarkable potential for capturing complex system behavior, yet achieving models that are both accurate and physically interpretable remains difficult. To address this, we propose Structured Kolmogorov-Arnold Neural ODEs (SKANODEs), a framework that integrates structured state-space modeling with Kolmogorov-Arnold Networks (KANs). Within a Neural ODE architecture, SKANODE employs a fully trainable KAN as a universal function approximator to perform virtual sensing, recovering latent states that correspond to interpretable physical quantities such as displacements and velocities. Leveraging KAN’s symbolic regression capability, SKANODE then extracts compact, interpretable expressions for the system’s governing dynamics. Experiments on two canonical nonlinear oscillators and a real-world F-16 ground vibration dataset demonstrate that SKANODE reliably recovers physically meaningful latent displacement and velocity trajectories from acceleration measurements, identifies the correct governing nonlinearities–including the cubic stiffness in the Duffing oscillator and the nonlinear damping structure in the Van der Pol oscillator–and reveals hysteretic signatures in the F-16 interface dynamics through structured latent phase portraits and an interpretable symbolic model. Across all three cases, SKANODE provides more accurate and robust predictions than black-box NODE baselines and classical ARX and NARX identification, while producing equation-level descriptions of the learned nonlinear dynamics.

QuKAN: A Quantum Circuit Born Machine approach to Quantum Kolmogorov Arnold Networks

Authors: Yannick Werner, Akash Malemath, Mengxi Liu, Vitor Fortes Rey, Nikolaos Palaiodimopoulos, Paul Lukowicz, Maximilian Kiefer-Emmanouilidis

Abstract: Kolmogorov Arnold Networks (KANs), built upon the Kolmogorov Arnold representation theorem (KAR), have demonstrated promising capabilities in expressing complex functions with fewer neurons. This is achieved by implementing learnable parameters on the edges instead of on the nodes, unlike traditional networks such as Multi-Layer Perceptrons (MLPs). However, KANs potential in quantum machine learning has not yet been well explored. In this work, we present an implementation of these KAN architectures in both hybrid and fully quantum forms using a Quantum Circuit Born Machine (QCBM). We adapt the KAN transfer using pre-trained residual functions, thereby exploiting the representational power of parametrized quantum circuits. In the hybrid model we combine classical KAN components with quantum subroutines, while the fully quantum version the entire architecture of the residual function is translated to a quantum model. We demonstrate the feasibility, interpretability and performance of the proposed Quantum KAN (QuKAN) architecture.

Optimization by VarQITE on Adaptive Variational Quantum Kolmogorov-Arnold Network

Authors: Hikaru Wakaura, Rahmat Mulyawan, Andriyan B. Suksmono

Abstract: Quantum imaginary time evolution (QITE) is a powerful method to derive the ground states of the systems. Only the damping of quantum states leads it; hence, reaching the ground state is guaranteed by nature without any external manipulation. Numerous QITE methods by many groups are used to improve speed and accuracy, derive excited states, and solve combined optimization problems. However, the QITE methods have not been used for quantum machine learning to predict the ideal values for multiple input values. Therefore, we propose a method for applying QITE methods for quantum machine learning and demonstrate fitting problems of elementary functions and classification problems on a 2-D plane. As a result, we confirmed that our method was more accurate than a quantum neural network in solving some problems. Our method can be used for other quantum machine learning algorithms; hence, it may be the milestone for applying QITE to quantum machine learning.

July

Five-Gene Expression Formula Accurately Detects Hepatocellular Carcinoma Tumors

Authors: Aram Ansary Ogholbake, Qiang Cheng

Abstract: Hepatocellular carcinoma (HCC) is one of the leading causes of cancer-related deaths worldwide. Several diagnostic methods, such as imaging modalities and Serum Alpha-Fetoprotein (AFP) testing, have been used for HCC detection; however, their effectiveness is limited to later stages of the disease. In contrast, transcriptomic analysis of biposy samples has shown promise for early detection. While machine learning techniques have been applied to transcriptomic data for cancer detection, their clinical adoption remains limited due to challenges such as poor generalizability across different datasets, lack of interpretability, and high computational complexity. To address these limitations, we developed a novel predictive formula for HCC detection using the Kolmogorov-Arnold Network (KAN). This formula is based on the expression levels of five genes: VIPR1, CYP1A2, FCN3, ECM1, and LIFR. Derived from the GSE25097 dataset, the formula offers a simple, interpretable, efficient, and accessible approach for HCC identification. It achieves 99% accuracy on the GSE25097 test set and demonstrates robust performance on six additional independent datasets, achieving accuracies of above 90% in all cases. These findings highlight the critical role of these five genes as biomarkers for HCC detection, offering a foundation for future research and clinical applications to improve HCC diagnostic approaches.

Variational Kolmogorov-Arnold Network

Authors: Francesco Alesiani, Henrik Christiansen, Federico Errica

Abstract: Kolmogorov-Arnold Networks (KANs) offer a theoretically grounded alternative to multi-layer perceptrons by representing multivariate functions as compositions of univariate basis functions. However, a critical limitation of KANs is the need to manually specify the number of basis functions per layer – a hyperparameter that directly controls model capacity and substantially impacts performance, yet whose optimal value varies unpredictably across tasks. We present InfinityKAN, a variational inference framework that eliminates this design choice by learning the number of basis functions during training. Our approach models the basis count as a latent variable with a truncated exponential prior, introducing a differentiable weighting function that enables gradient-based optimization. We establish the Lipschitz continuity of the variational objective, ensuring stable training dynamics. Experiments across 18 datasets spanning synthetic, image, tabular, and graph domains demonstrate that InfinityKAN matches or exceeds the performance of KANs while requiring no manual selection of the number of bases for each layer.

Towards Interpretable PolSAR Image Classification: Polarimetric Scattering Mechanism Informed Concept Bottleneck and Kolmogorov-Arnold Network

Authors: Jinqi Zhang, Fangzhou Han, Di Zhuang, Lamei Zhang, Bin Zou, Li Yuan

Abstract: In recent years, Deep Learning (DL) based methods have received extensive and sufficient attention in the field of PolSAR image classification, which show excellent performance. However, due to the ``black-box” nature of DL methods, the interpretation of the high-dimensional features extracted and the backtracking of the decision-making process based on the features are still unresolved problems. In this study, we first highlight this issue and attempt to achieve the interpretability analysis of DL-based PolSAR image classification technology with the help of Polarimetric Target Decomposition (PTD), a feature extraction method related to the scattering mechanism unique to the PolSAR image processing field. In our work, by constructing the polarimetric conceptual labels and a novel structure named Parallel Concept Bottleneck Networks (PaCBM), the uninterpretable high-dimensional features are transformed into human-comprehensible concepts based on physically verifiable polarimetric scattering mechanisms. Then, the Kolmogorov-Arnold Network (KAN) is used to replace Multi-Layer Perceptron (MLP) for achieving a more concise and understandable mapping process between layers and further enhanced non-linear modeling ability. The experimental results on several PolSAR datasets show that the features could be conceptualization under the premise of achieving satisfactory accuracy through the proposed pipeline, and the analytical function for predicting category labels from conceptual labels can be obtained by combining spline functions, thus promoting the research on the interpretability of the DL-based PolSAR image classification model.

Exploring Kolmogorov-Arnold Network Expansions in Vision Transformers for Mitigating Catastrophic Forgetting in Continual Learning

Authors: Zahid Ullah, Jihie Kim

Abstract: Continual learning (CL), the ability of a model to learn new tasks without forgetting previously acquired knowledge, remains a critical challenge in artificial intelligence, particularly for vision transformers (ViTs) utilizing Multilayer Perceptrons (MLPs) for global representation learning. Catastrophic forgetting, where new information overwrites prior knowledge, is especially problematic in these models. This research proposes replacing MLPs in ViTs with Kolmogorov-Arnold Network (KANs) to address this issue. KANs leverage local plasticity through spline-based activations, ensuring that only a subset of parameters is updated per sample, thereby preserving previously learned knowledge. The study investigates the efficacy of KAN-based ViTs in CL scenarios across benchmark datasets (MNIST, CIFAR100), focusing on their ability to retain accuracy on earlier tasks while adapting to new ones. Experimental results demonstrate that KAN-based ViTs significantly mitigate catastrophic forgetting, outperforming traditional MLP-based ViTs in knowledge retention and task adaptation. This novel integration of KANs into ViTs represents a promising step toward more robust and adaptable models for dynamic environments.

Bridging KAN and MLP: MJKAN, a Hybrid Architecture with Both Efficiency and Expressiveness

Authors: Hanseon Joo, Hayoung Choi, Ook Lee, Minjong Cheon

Abstract: Kolmogorov-Arnold Networks (KANs) have garnered attention for replacing fixed activation functions with learnable univariate functions, but they exhibit practical limitations, including high computational costs and performance deficits in general classification tasks. In this paper, we propose the Modulation Joint KAN (MJKAN), a novel neural network layer designed to overcome these challenges. MJKAN integrates a FiLM (Feature-wise Linear Modulation)-like mechanism with Radial Basis Function (RBF) activations, creating a hybrid architecture that combines the non-linear expressive power of KANs with the efficiency of Multilayer Perceptrons (MLPs). We empirically validated MJKAN’s performance across a diverse set of benchmarks, including function regression, image classification (MNIST, CIFAR-10/100), and natural language processing (AG News, SMS Spam). The results demonstrate that MJKAN achieves superior approximation capabilities in function regression tasks, significantly outperforming MLPs, with performance improving as the number of basis functions increases. Conversely, in image and text classification, its performance was competitive with MLPs but revealed a critical dependency on the number of basis functions. We found that a smaller basis size was crucial for better generalization, highlighting that the model’s capacity must be carefully tuned to the complexity of the data to prevent overfitting. In conclusion, MJKAN offers a flexible architecture that inherits the theoretical advantages of KANs while improving computational efficiency and practical viability.

Capsule-ConvKAN: A Hybrid Neural Approach to Medical Image Classification

Authors: Laura Pituková, Peter Sinčák, László József Kovács, Peng Wang

Abstract: This study conducts a comprehensive comparison of four neural network architectures: Convolutional Neural Network, Capsule Network, Convolutional Kolmogorov-Arnold Network, and the newly proposed Capsule-Convolutional Kolmogorov-Arnold Network. The proposed Capsule-ConvKAN architecture combines the dynamic routing and spatial hierarchy capabilities of Capsule Network with the flexible and interpretable function approximation of Convolutional Kolmogorov-Arnold Networks. This novel hybrid model was developed to improve feature representation and classification accuracy, particularly in challenging real-world biomedical image data. The architectures were evaluated on a histopathological image dataset, where Capsule-ConvKAN achieved the highest classification performance with an accuracy of 91.21%. The results demonstrate the potential of the newly introduced Capsule-ConvKAN in capturing spatial patterns, managing complex features, and addressing the limitations of traditional convolutional models in medical image classification.

KAConvText: Novel Approach to Burmese Sentence Classification using Kolmogorov-Arnold Convolution

Authors: Ye Kyaw Thu, Thura Aung, Thazin Myint Oo, Thepchai Supnithi

Abstract: This paper presents the first application of Kolmogorov-Arnold Convolution for Text (KAConvText) in sentence classification, addressing three tasks: imbalanced binary hate speech detection, balanced multiclass news classification, and imbalanced multiclass ethnic language identification. We investigate various embedding configurations, comparing random to fastText embeddings in both static and fine-tuned settings, with embedding dimensions of 100 and 300 using CBOW and Skip-gram models. Baselines include standard CNNs and CNNs augmented with a Kolmogorov-Arnold Network (CNN-KAN). In addition, we investigated KAConvText with different classification heads - MLP and KAN, where using KAN head supports enhanced interpretability. Results show that KAConvText-MLP with fine-tuned fastText embeddings achieves the best performance of 91.23% accuracy (F1-score = 0.9109) for hate speech detection, 92.66% accuracy (F1-score = 0.9267) for news classification, and 99.82% accuracy (F1-score = 0.9982) for language identification.

DMF2Mel: A Dynamic Multiscale Fusion Network for EEG-Driven Mel Spectrogram Reconstruction

Authors: Cunhang Fan, Sheng Zhang, Jingjing Zhang, Enrui Liu, Xinhui Li, Gangming Zhao, Zhao Lv

Abstract: Decoding speech from brain signals is a challenging research problem. Although existing technologies have made progress in reconstructing the mel spectrograms of auditory stimuli at the word or letter level, there remain core challenges in the precise reconstruction of minute-level continuous imagined speech: traditional models struggle to balance the efficiency of temporal dependency modeling and information retention in long-sequence decoding. To address this issue, this paper proposes the Dynamic Multiscale Fusion Network (DMF2Mel), which consists of four core components: the Dynamic Contrastive Feature Aggregation Module (DC-FAM), the Hierarchical Attention-Guided Multi-Scale Network (HAMS-Net), the SplineMap attention mechanism, and the bidirectional state space module (convMamba). Specifically, the DC-FAM separates speech-related “foreground features” from noisy “background features” through local convolution and global attention mechanisms, effectively suppressing interference and enhancing the representation of transient signals. HAMS-Net, based on the U-Net framework,achieves cross-scale fusion of high-level semantics and low-level details. The SplineMap attention mechanism integrates the Adaptive Gated Kolmogorov-Arnold Network (AGKAN) to combine global context modeling with spline-based local fitting. The convMamba captures long-range temporal dependencies with linear complexity and enhances nonlinear dynamic modeling capabilities. Results on the SparrKULee dataset show that DMF2Mel achieves a Pearson correlation coefficient of 0.074 in mel spectrogram reconstruction for known subjects (a 48% improvement over the baseline) and 0.048 for unknown subjects (a 35% improvement over the baseline).Code is available at: https://github.com/fchest/DMF2Mel.

Minimum-norm interpolation for unknown surface reconstruction

Authors: Alex Shiu Lun Chu, Leevan Ling, Ka Chun Cheung

Abstract: We study algorithms to estimate geometric properties of raw point cloud data through implicit surface representations. Given that any level-set function with a constant level set corresponding to the surface can be used for such estimations, numerical methods need not specify a unique target function for these domain-type interpolation problems. In this paper, we focus on kernel-based interpolation by radial basis functions (RBF) and reformulate the uniquely solvable interpolation problem into a constrained optimization model. This model minimizes some user-defined norm while enforcing all interpolation conditions. To enable nontrivial feasible solutions, we propose to enhance the trial space with 1D kernel basis functions inspired by Kolmogorov-Arnold Networks (KANs). Numerical experiments demonstrate that our proposed mixed-dimensional trial space significantly improves surface reconstruction from raw point clouds. This is particularly evident in the precise estimation of surface normals, outperforming traditional RBF trial spaces including the one for Hermite interpolation. This framework not only enhances processing of raw point cloud data but also shows potential for further contributions to computational geometry. We demonstrate this with a point cloud processing example.

Application of interpretable data-driven methods for the reconstruction of supernova neutrino energy spectra following fast neutrino flavor conversions

Authors: Haihao Shi, Zhenyang Huang, Qiyu Yan, Junda Zhou, Guoliang Lü, Xuefei Chen

Abstract: Neutrinos can experience fast flavor conversions (FFCs) in highly dense astrophysical environments, such as core-collapse supernovae and neutron star mergers, potentially affecting energy transport and other processes. Simulating fast flavor conversions under realistic astrophysical conditions requires substantial computational resources and poses significant analytical challenges. While machine learning methods such as multilayer perceptrons have been used to accurately predict the asymptotic outcomes of FFCs, their “black-box” nature limits the extraction of direct physical insight. To mitigate this limitation, we employ two distinct interpretable machine learning frameworks, Kolmogorov-Arnold Networks (KANs) and Sparse Identification of Nonlinear Dynamics (SINDy), to learn interpretable surrogates for the asymptotic input-output mapping from an FFC simulation dataset. Our analysis reveals a fundamental trade-off between predictive accuracy and model simplicity. KANs demonstrate high fidelity in reconstructing post-conversion neutrino energy spectra, achieving accuracies of up to 90%. In contrast, SINDy yields a low-rank, compact closed-form approximation of the input-output mapping, at the expense of some predictive accuracy. Critically, using these structured and sparse surrogates as diagnostic tools, we identify that the system’s evolution is most sensitive to the initial number density of heavy-lepton neutrinos when FFCs are triggered, compared with other physical quantities. Ultimately, this work provides a methodological framework for interpretable machine learning that supports genuine data-driven scientific discovery in astronomy and astrophysics, going beyond prediction alone.

Contrastive-KAN: A Semi-Supervised Intrusion Detection Framework for Cybersecurity with scarce Labeled Data

Authors: Mohammad Alikhani, Reza Kazemi

Abstract: In the era of the Fourth Industrial Revolution, cybersecurity and intrusion detection systems are vital for the secure and reliable operation of IoT and IIoT environments. A key challenge in this domain is the scarcity of labeled cyberattack data, as most industrial systems operate under normal conditions. This data imbalance, combined with the high cost of annotation, hinders the effective training of machine learning models. Moreover, the rapid detection of attacks is essential, especially in critical infrastructure, to prevent large-scale disruptions. To address these challenges, we propose a real-time intrusion detection system based on a semi-supervised contrastive learning framework using the Kolmogorov-Arnold Network (KAN). Our method leverages abundant unlabeled data to effectively distinguish between normal and attack behaviors. We validate our approach on three benchmark datasets, UNSW-NB15, BoT-IoT, and Gas Pipeline, using only 2.20%, 1.28%, and 8% of labeled samples, respectively, to simulate real-world conditions. Experimental results show that our method outperforms existing contrastive learning-based approaches. We further compare KAN with a traditional multilayer perceptron (MLP), demonstrating KAN’s superior performance in both detection accuracy and robustness under limited supervision. KAN’s ability to model complex relationships, along with its learnable activation functions, is also explored and visualized, offering interpretability and the potential for rule extraction. The method supports multi-class classification and proves effective in safety, critical environments where reliability is paramount.

A Lightweight Gradient-based Causal Discovery Framework with Applications to Complex Industrial Processes

Authors: Meiliang Liu, Huiwen Dong, Xiaoxiao Yang, Yunfang Xu, Zijin Li, Zhengye Si, Xinyue Yang, Zhiwen Zhao

Abstract: With the advancement of deep learning technologies, various neural network-based Granger causality models have been proposed. Although these models have demonstrated notable improvements, several limitations remain. Most existing approaches adopt the component-wise architecture, necessitating the construction of a separate model for each time series, which results in substantial computational costs. In addition, imposing the sparsity-inducing penalty on the first-layer weights of the neural network to extract causal relationships weakens the model’s ability to capture complex interactions. To address these limitations, we propose Gradient Regularization-based Neural Granger Causality (GRNGC), which requires only one time series prediction model and applies $L_{1}$ regularization to the gradient between model’s input and output to infer Granger causality. Moreover, GRNGC is not tied to a specific time series forecasting model and can be implemented with diverse architectures such as KAN, MLP, and LSTM, offering enhanced flexibility. Numerical simulations on DREAM, Lorenz-96, fMRI BOLD, and CausalTime show that GRNGC outperforms existing baselines and significantly reduces computational overhead. Meanwhile, experiments on real-world DNA, Yeast, HeLa, and bladder urothelial carcinoma datasets further validate the model’s effectiveness in reconstructing gene regulatory networks.

FORTRESS: Function-composition Optimized Real-Time Resilient Structural Segmentation via Kolmogorov-Arnold Enhanced Spatial Attention Networks

Authors: Christina Thrainer, Md Meftahul Ferdaus, Mahdi Abdelguerfi, Christian Guetl, Steven Sloan, Kendall N. Niles, Ken Pathak

Abstract: Automated structural defect segmentation in civil infrastructure faces a critical challenge: achieving high accuracy while maintaining computational efficiency for real-time deployment. This paper presents FORTRESS (Function-composition Optimized Real-Time Resilient Structural Segmentation), a new architecture that balances accuracy and speed by using a special method that combines depthwise separable convolutions with adaptive Kolmogorov-Arnold Network integration. FORTRESS incorporates three key innovations: a systematic depthwise separable convolution framework achieving a 3.6x parameter reduction per layer, adaptive TiKAN integration that selectively applies function composition transformations only when computationally beneficial, and multi-scale attention fusion combining spatial, channel, and KAN-enhanced features across decoder levels. The architecture achieves remarkable efficiency gains with 91% parameter reduction (31M to 2.9M), 91% computational complexity reduction (13.7 to 1.17 GFLOPs), and 3x inference speed improvement while delivering superior segmentation performance. Evaluation on benchmark infrastructure datasets demonstrates state-of-the-art results with an F1- score of 0.771 and a mean IoU of 0.677, significantly outperforming existing methods including U-Net, SA-UNet, and U- KAN. The dual optimization strategy proves essential for optimal performance, establishing FORTRESS as a robust solution for practical structural defect segmentation in resource-constrained environments where both accuracy and computational efficiency are paramount. Comprehensive architectural specifications are provided in the Supplemental Material. Source code is available at URL: https://github.com/faeyelab/fortress-paper-code.

Improving KAN with CDF normalization to quantiles

Authors: Jakub Strawa, Jarek Duda

Abstract: Data normalization is crucial in machine learning, usually performed by subtracting the mean and dividing by standard deviation, or by rescaling to a fixed range. In copula theory, popular in finance, there is used normalization to approximately quantiles by transforming x to CDF(x) with estimated CDF (cumulative distribution function) to nearly uniform distribution in [0,1], allowing for simpler representations which are less likely to overfit. It seems nearly unknown in machine learning, therefore, we would like to present some its advantages on example of recently popular Kolmogorov-Arnold Networks (KANs), improving predictions from Legendre-KAN by just switching rescaling to CDF normalization. Additionally, in HCR interpretation, weights of such neurons are mixed moments providing local joint distribution models, allow to propagate also probability distributions, and change propagation direction.

Kolmogorov-Arnold Networks-based GRU and LSTM for Loan Default Early Prediction

Authors: Yue Yang, Zihan Su, Ying Zhang, Chang Chuan Goh, Yuxiang Lin, Anthony Graham Bellotti, Boon Giin Lee

Abstract: This study addresses a critical challenge in time series anomaly detection: enhancing the predictive capability of loan default models more than three months in advance to enable early identification of default events, helping financial institutions implement preventive measures before risk events materialize. Existing methods have significant drawbacks, such as their lack of accuracy in early predictions and their dependence on training and testing within the same year and specific time frames. These issues limit their practical use, particularly with out-of-time data. To address these, the study introduces two innovative architectures, GRU-KAN and LSTM-KAN, which merge Kolmogorov-Arnold Networks (KAN) with Gated Recurrent Units (GRU) and Long Short-Term Memory (LSTM) networks. The proposed models were evaluated against the baseline models (LSTM, GRU, LSTM-Attention, and LSTM-Transformer) in terms of accuracy, precision, recall, F1 and AUC in different lengths of feature window, sample sizes, and early prediction intervals. The results demonstrate that the proposed model achieves a prediction accuracy of over 92% three months in advance and over 88% eight months in advance, significantly outperforming existing baselines.

Kolmogorov Arnold Networks (KANs) for Imbalanced Data – An Empirical Perspective

Authors: Pankaj Yadav, Vivek Vijay

Abstract: Kolmogorov Arnold Networks (KANs) are recent architectural advancement in neural computation that offer a mathematically grounded alternative to standard neural networks. This study presents an empirical evaluation of KANs in context of class imbalanced classification, using ten benchmark datasets. We observe that KANs can inherently perform well on raw imbalanced data more effectively than Multi-Layer Perceptrons (MLPs) without any resampling strategy. However, conventional imbalance strategies fundamentally conflict with KANs mathematical structure as resampling and focal loss implementations significantly degrade KANs performance, while marginally benefiting MLPs. Crucially, KANs suffer from prohibitive computational costs without proportional performance gains. Statistical validation confirms that MLPs with imbalance techniques achieve equivalence with KANs (|d| < 0.08 across metrics) at minimal resource costs. These findings reveal that KANs represent a specialized solution for raw imbalanced data where resources permit. But their severe performance-resource tradeoffs and incompatibility with standard resampling techniques currently limits practical deployment. We identify critical research priorities as developing KAN specific architectural modifications for imbalance learning, optimizing computational efficiency, and theoretical reconciling their conflict with data augmentation. This work establishes foundational insights for next generation KAN architectures in imbalanced classification scenarios.

CKANIO: Learnable Chebyshev Polynomials for Inertial Odometry

Authors: Shanshan Zhang, Siyue Wang, Tianshui Wen, Liqin Wu, Qi Zhang, Ziheng Zhou, Ao Peng, Xuemin Hong, Lingxiang Zheng, Yu Yang

Abstract: Inertial odometry (IO) relies exclusively on signals from an inertial measurement unit (IMU) for localization and offers a promising avenue for consumer grade positioning. However, accurate modeling of the nonlinear motion patterns present in IMU signals remains the principal limitation on IO accuracy. To address this challenge, we propose CKANIO, an IO framework that integrates Chebyshev based Kolmogorov-Arnold Networks (Chebyshev KAN). Specifically, we design a novel residual architecture that leverages the nonlinear approximation capabilities of Chebyshev polynomials within the KAN framework to more effectively model the complex motion characteristics inherent in IMU signals. To the best of our knowledge, this work represents the first application of an interpretable KAN model to IO. Experimental results on five publicly available datasets demonstrate the effectiveness of CKANIO.

KASPER: Kolmogorov Arnold Networks for Stock Prediction and Explainable Regimes

Authors: Vidhi Oad, Param Pathak, Nouhaila Innan, Shalini D, Muhammad Shafique

Abstract: Forecasting in financial markets remains a significant challenge due to their nonlinear and regime-dependent dynamics. Traditional deep learning models, such as long short-term memory networks and multilayer perceptrons, often struggle to generalize across shifting market conditions, highlighting the need for a more adaptive and interpretable approach. To address this, we introduce Kolmogorov-Arnold networks for stock prediction and explainable regimes (KASPER), a novel framework that integrates regime detection, sparse spline-based function modeling, and symbolic rule extraction. The framework identifies hidden market conditions using a Gumbel-Softmax-based mechanism, enabling regime-specific forecasting. For each regime, it employs Kolmogorov-Arnold networks with sparse spline activations to capture intricate price behaviors while maintaining robustness. Interpretability is achieved through symbolic learning based on Monte Carlo Shapley values, which extracts human-readable rules tailored to each regime. Applied to real-world financial time series from Yahoo Finance, the model achieves an $R^2$ score of 0.89, a Sharpe Ratio of 12.02, and a mean squared error as low as 0.0001, outperforming existing methods. This research establishes a new direction for regime-aware, transparent, and robust forecasting in financial markets.

Kolmogorov Arnold Network Autoencoder in Medicine

Authors: Ugo Lomoio, Pierangelo Veltri, Pietro Hiram Guzzi

Abstract: Deep learning neural networks architectures such Multi Layer Perceptrons (MLP) and Convolutional blocks still play a crucial role in nowadays research advancements. From a topological point of view, these architecture may be represented as graphs in which we learn the functions related to the nodes while fixed edges convey the information from the input to the output. A recent work introduced a new architecture called Kolmogorov Arnold Networks (KAN) that reports how putting learnable activation functions on the edges of the neural network leads to better performances in multiple scenarios. Multiple studies are focusing on optimizing the KAN architecture by adding important features such as dropout regularization, Autoencoders (AE), model benchmarking and last, but not least, the KAN Convolutional Network (KCN) that introduced matrix convolution with KANs learning. This study aims to benchmark multiple versions of vanilla AEs (such as Linear, Convolutional and Variational) against their Kolmogorov-Arnold counterparts that have same or less number of parameters. Using cardiological signals as model input, a total of five different classic AE tasks were studied: reconstruction, generation, denoising, inpainting and anomaly detection. The proposed experiments uses a medical dataset \textit{AbnormalHeartbeat} that contains audio signals obtained from the stethoscope.

Universal Relation Between Quantum Entanglement and Particle Transport

Authors: Elvira Bilokon, Valeriia Bilokon, Abhijit Sen, Mohammed Th. Hassan, Andrii Sotnikov, Denys I. Bondar

Abstract: Entanglement entropy is a fundamental measure of quantum correlations and a key resource underpinning advances in quantum information and many-body physics. We uncover a universal relationship between bipartite entanglement entropy and particle number after the barrier in a one-dimensional Fermi-Hubbard system with an external asymmetric potential. Using Kolmogorov-Arnold Networks - a novel machine learning architecture - we learn this relationship across a broad range of interaction strengths with near-perfect predictive accuracy. Furthermore, we propose a simple analytical binary-entropy-like expression that quantitatively captures the observed correlation for fixed parameters. Our findings open new avenues for characterizing quantum correlations in transport phenomena and provide a powerful framework for predicting entanglement evolution in quantum systems.

Multi-Resolution Training-Enhanced Kolmogorov-Arnold Networks for Multi-Scale PDE Problems

Authors: Yu-Sen Yang, Ling Guo, Xiaodan Ren

Abstract: Multi-scale PDE problems present significant challenges in scientific computing. While conventional MLP-based deep learning methods exhibit spectral bias in resolving multi-scale features, the physics-informed Kolmogorov-Arnold network (PIKAN) mitigates this issue through its novel architecture, demonstrating certain advantages. On the other hand, insights from the information bottleneck theory suggest that high-resolution training points are essential for these hybrid methods to accurately capture multi-scale behavior, although this requirement often leads to longer training times. To address this challenge, we propose a simple yet effective multi-resolution training-enhanced PIKAN framework, termed MR-PIKAN, which trains the data-physics hybrid model either sequentially or alternately across different resolutions. The proposed MR-PIKAN is validated on various multi-scale forward and inverse PDE problems. Numerical results indicate that this new training strategy effectively reduces computational costs without sacrificing accuracy, thereby enabling efficient solutions of complex multi-scale PDEs in both forward and inverse settings.

A holomorphic Kolmogorov-Arnold network framework for solving elliptic problems on arbitrary 2D domains

Authors: Matteo Calafà, Tito Andriollo, Allan P. Engsig-Karup, Cheol-Ho Jeong

Abstract: Physics-informed holomorphic neural networks (PIHNNs) have recently emerged as efficient surrogate models for solving differential problems. By embedding the underlying problem structure into the network, PIHNNs require training only to satisfy boundary conditions, often resulting in significantly improved accuracy and computational efficiency compared to traditional physics-informed neural networks (PINNs). In this work, we improve and extend the application of PIHNNs to two-dimensional problems. First, we introduce a novel holomorphic network architecture based on the Kolmogorov-Arnold representation (PIHKAN), which achieves higher accuracy with reduced model complexity. Second, we develop mathematical extensions that broaden the applicability of PIHNNs to a wider class of elliptic partial differential equations, including the Helmholtz equation. Finally, we propose a new method based on Laurent series theory that enables the application of holomorphic networks to multiply-connected plane domains, thereby removing the previous limitation to simply-connected geometries.

Scientific Machine Learning with Kolmogorov-Arnold Networks

Authors: Salah A. Faroughi, Farinaz Mostajeran, Amin Hamed Mashhadzadeh, Shirko Faroughi

Abstract: The field of scientific machine learning, which originally utilized multilayer perceptrons (MLPs), is increasingly adopting Kolmogorov-Arnold Networks (KANs) for data encoding. This shift is driven by the limitations of MLPs, including poor interpretability, fixed activation functions, and difficulty capturing localized or high-frequency features. KANs address these issues with enhanced interpretability and flexibility, enabling more efficient modeling of complex nonlinear interactions and effectively overcoming the constraints associated with conventional MLP architectures. This review categorizes recent progress in KAN-based models across three distinct perspectives: (i) data-driven learning, (ii) physics-informed modeling, and (iii) deep-operator learning. Each perspective is examined through the lens of architectural design, training strategies, application efficacy, and comparative evaluation against MLP-based counterparts. By benchmarking KANs against MLPs, we highlight consistent improvements in accuracy, convergence, and spectral representation, clarifying KANs’ advantages in capturing complex dynamics while learning more effectively. In addition to reviewing recent literature, this work also presents several comparative evaluations that clarify central characteristics of KAN modeling and hint at their potential implications for real-world applications. Finally, this review identifies critical challenges and open research questions in KAN development, particularly regarding computational efficiency, theoretical guarantees, hyperparameter tuning, and algorithm complexity. We also outline future research directions aimed at improving the robustness, scalability, and physical consistency of KAN-based frameworks.

Beyond Linear Bottlenecks: Spline-Based Knowledge Distillation for Culturally Diverse Art Style Classification

Authors: Abdellah Zakaria Sellam, Salah Eddine Bekhouche, Cosimo Distante, Abdelmalik Taleb-Ahmed

Abstract: Art style classification remains a formidable challenge in computational aesthetics due to the scarcity of expertly labeled datasets and the intricate, often nonlinear interplay of stylistic elements. While recent dual-teacher self-supervised frameworks reduce reliance on labeled data, their linear projection layers and localized focus struggle to model global compositional context and complex style-feature interactions. We enhance the dual-teacher knowledge distillation framework to address these limitations by replacing conventional MLP projection and prediction heads with Kolmogorov-Arnold Networks (KANs). Our approach retains complementary guidance from two teacher networks, one emphasizing localized texture and brushstroke patterns, the other capturing broader stylistic hierarchies while leveraging KANs’ spline-based activations to model nonlinear feature correlations with mathematical precision. Experiments on WikiArt and Pandora18k demonstrate that our approach outperforms the base dual teacher architecture in Top-1 accuracy. Our findings highlight the importance of KANs in disentangling complex style manifolds, leading to better linear probe accuracy than MLP projections.

August

Sinusoidal Approximation Theorem for Kolmogorov-Arnold Networks

Authors: Sergei Gleyzer, Hanh Nguyen, Dinesh P. Ramakrishnan, Eric A. F. Reinhardt

Abstract: The Kolmogorov-Arnold representation theorem states that any continuous multivariable function can be exactly represented as a finite superposition of continuous single variable functions. Subsequent simplifications of this representation involve expressing these functions as parameterized sums of a smaller number of unique monotonic functions. These developments led to the proof of the universal approximation capabilities of multilayer perceptron networks with sigmoidal activations, forming the alternative theoretical direction of most modern neural networks. Kolmogorov-Arnold Networks (KANs) have been recently proposed as an alternative to multilayer perceptrons. KANs feature learnable nonlinear activations applied directly to input values, modeled as weighted sums of basis spline functions. This approach replaces the linear transformations and sigmoidal post-activations used in traditional perceptrons. Subsequent works have explored alternatives to spline-based activations. In this work, we propose a novel KAN variant by replacing both the inner and outer functions in the Kolmogorov-Arnold representation with weighted sinusoidal functions of learnable frequencies. Inspired by simplifications introduced by Lorentz and Sprecher, we fix the phases of the sinusoidal activations to linearly spaced constant values and provide a proof of its theoretical validity. We also conduct numerical experiments to evaluate its performance on a range of multivariable functions, comparing it with fixed-frequency Fourier transform methods and multilayer perceptrons (MLPs). We show that it outperforms the fixed-frequency Fourier transform and achieves comparable performance to MLPs.

KFS: KAN based adaptive Frequency Selection learning architecture for long term time series forecasting

Authors: Changning Wu, Gao Wu, Rongyao Cai, Yong Liu, Kexin Zhang

Abstract: Multi-scale decomposition architectures have emerged as predominant methodologies in time series forecasting. However, real-world time series exhibit noise interference across different scales, while heterogeneous information distribution among frequency components at varying scales leads to suboptimal multi-scale representation. Inspired by Kolmogorov-Arnold Networks (KAN) and Parseval’s theorem, we propose a KAN based adaptive Frequency Selection learning architecture (KFS) to address these challenges. This framework tackles prediction challenges stemming from cross-scale noise interference and complex pattern modeling through its FreK module, which performs energy-distribution-based dominant frequency selection in the spectral domain. Simultaneously, KAN enables sophisticated pattern representation while timestamp embedding alignment synchronizes temporal representations across scales. The feature mixing module then fuses scale-specific patterns with aligned temporal features. Extensive experiments across multiple real-world time series datasets demonstrate that KT achieves state-of-the-art performance as a simple yet effective architecture.

KANMixer: a minimal KAN-centered mixer for long-term time series forecasting

Authors: Lingyu Jiang, Dengzhe Hou, Yuping Wang, Yao Su, Shuo Xing, Wenjing Chen, Xin Zhang, Zhengzhong Tu, Ziming Zhang, Fangzhou Lin, Michael Zielewski, Kazunori D Yamada

Abstract: Long-term time series forecasting (LTSF) underpins critical applications from energy management to weather prediction, yet achieving reliable multi-step-ahead accuracy remains challenging. Existing LTSF approaches, dominated by MLP- and Transformer-based architectures, either rely on simple linear mappings or introduce increasingly complex hand-crafted inductive biases, raising the question of whether a more expressive and principled nonlinear core could offer a better alternative. Therefore, we investigate whether Kolmogorov-Arnold Networks (KANs), a recently proposed model featuring adaptive basis functions capable of granular modulation of nonlinearities, can improve LTSF performance, and under which design choices they are most effective. Specifically, we propose KANMixer, a minimal KAN-centered architecture consisting of a multi-scale pooling frontend, a KAN-based temporal mixing backbone, and prediction heads. By avoiding heavy auxiliary modules, KANMixer enables a clear assessment of KAN components in LTSF. Across 28 benchmark-horizon settings against nine baselines, KANMixer achieves the best MSE in 16 settings and the best MAE in 11. Furthermore, extensive ablations on three representative datasets show that KAN effectiveness depends strongly on the choice of edge function; B-spline bases outperform Fourier and Wavelet alternatives; the prediction head contributes most to the gains; moderate depth is preferred over deeper unstable stacks; and decomposition priors help MLP but harm KAN. Beyond practical guidance for integrating KAN into LTSF, these results reveal an underexplored dependency between structural priors and backbone nonlinearity: design choices that benefit MLP can degrade KAN.

Comparative Evaluation of Kolmogorov-Arnold Autoencoders and Orthogonal Autoencoders for Fault Detection with Varying Training Set Sizes

Authors: Enrique Luna Villagómez, Vladimir Mahalec

Abstract: Kolmogorov-Arnold Networks (KANs) have recently emerged as a flexible and parameter-efficient alternative to conventional neural networks. Unlike standard architectures that use fixed node-based activations, KANs place learnable functions on edges, parameterized by different function families. While they have shown promise in supervised settings, their utility in unsupervised fault detection remains largely unexplored. This study presents a comparative evaluation of KAN-based autoencoders (KAN-AEs) for unsupervised fault detection in chemical processes. We investigate four KAN-AE variants, each based on a different KAN implementation (EfficientKAN, FastKAN, FourierKAN, and WavKAN), and benchmark them against an Orthogonal Autoencoder (OAE) on the Tennessee Eastman Process. Models are trained on normal operating data across 13 training set sizes and evaluated on 21 fault types, using Fault Detection Rate (FDR) as the performance metric. WavKAN-AE achieves the highest overall FDR ($\geq$92\%) using just 4,000 training samples and remains the top performer, even as other variants are trained on larger datasets. EfficientKAN-AE reaches $\geq$90\% FDR with only 500 samples, demonstrating robustness in low-data settings. FastKAN-AE becomes competitive at larger scales ($\geq$50,000 samples), while FourierKAN-AE consistently underperforms. The OAE baseline improves gradually but requires substantially more data to match top KAN-AE performance. These results highlight the ability of KAN-AEs to combine data efficiency with strong fault detection performance. Their use of structured basis functions suggests potential for improved model transparency, making them promising candidates for deployment in data-constrained industrial settings.

Unifying Locality of KANs and Feature Drift Compensation Projection for Data-free Replay based Continual Face Forgery Detection

Authors: Tianshuo Zhang, Siran Peng, Li Gao, Haoyuan Zhang, Xiangyu Zhu, Zhen Lei

Abstract: The rapid advancements in face forgery techniques necessitate that detectors continuously adapt to new forgery methods, thus situating face forgery detection within a continual learning paradigm. However, when detectors learn new forgery types, their performance on previous types often degrades rapidly, a phenomenon known as catastrophic forgetting. Kolmogorov-Arnold Networks (KANs) utilize locally plastic splines as their activation functions, enabling them to learn new tasks by modifying only local regions of the functions while leaving other areas unaffected. Therefore, they are naturally suitable for addressing catastrophic forgetting. However, KANs have two significant limitations: 1) the splines are ineffective for modeling high-dimensional images, while alternative activation functions that are suitable for images lack the essential property of locality; 2) in continual learning, when features from different domains overlap, the mapping of different domains to distinct curve regions always collapses due to repeated modifications of the same regions. In this paper, we propose a KAN-based Continual Face Forgery Detection (KAN-CFD) framework, which includes a Domain-Group KAN Detector (DG-KD) and a data-free replay Feature Separation strategy via KAN Drift Compensation Projection (FS-KDCP). DG-KD enables KANs to fit high-dimensional image inputs while preserving locality and local plasticity. FS-KDCP avoids the overlap of the KAN input spaces without using data from prior tasks. Experimental results demonstrate that the proposed method achieves superior performance while notably reducing forgetting.

BubbleOKAN: A Physics-Informed Interpretable Neural Operator for High-Frequency Bubble Dynamics

Authors: Yunhao Zhang, Sidharth S. Menon, Lin Cheng, Aswin Gnanaskandan, Ameya D. Jagtap

Abstract: In this work, we employ physics-informed neural operators to map pressure profiles from an input function space to the corresponding bubble radius responses. Our approach employs a two-step DeepONet architecture. To address the intrinsic spectral bias of deep learning models, our model incorporates the Rowdy adaptive activation function, enhancing the representation of high-frequency features. Moreover, we introduce the Kolmogorov-Arnold network (KAN) based two-step DeepOKAN model, which enhances interpretability (often lacking in conventional multilayer perceptron architectures) while efficiently capturing high-frequency bubble dynamics without explicit utilization of activation functions in any form. We particularly investigate the use of spline basis functions in combination with radial basis functions (RBF) within our architecture, as they demonstrate superior performance in constructing a universal basis for approximating high-frequency bubble dynamics compared to alternative formulations. Furthermore, we emphasize on the performance bottleneck of RBF while learning the high frequency bubble dynamics and showcase the advantage of using spline basis function for the trunk network in overcoming this inherent spectral bias. The model is systematically evaluated across three representative scenarios: (1) bubble dynamics governed by the Rayleigh-Plesset equation with a single initial radius, (2) bubble dynamics governed by the Keller-Miksis equation with a single initial radius, and (3) Keller-Miksis dynamics with multiple initial radii. We also compare our results with state-of-the-art neural operators, including Fourier Neural Operators, Wavelet Neural Operators, OFormer, and Convolutional Neural Operators. Our findings demonstrate that the two-step DeepOKAN accurately captures both low- and high-frequency behaviors, and offers a promising alternative to conventional numerical solvers.

LuKAN: A Kolmogorov-Arnold Network Framework for 3D Human Motion Prediction

Authors: Md Zahidul Hasan, A. Ben Hamza, Nizar Bouguila

Abstract: The goal of 3D human motion prediction is to forecast future 3D poses of the human body based on historical motion data. Existing methods often face limitations in achieving a balance between prediction accuracy and computational efficiency. In this paper, we present LuKAN, an effective model based on Kolmogorov-Arnold Networks (KANs) with Lucas polynomial activations. Our model first applies the discrete wavelet transform to encode temporal information in the input motion sequence. Then, a spatial projection layer is used to capture inter-joint dependencies, ensuring structural consistency of the human body. At the core of LuKAN is the Temporal Dependency Learner, which employs a KAN layer parameterized by Lucas polynomials for efficient function approximation. These polynomials provide computational efficiency and an enhanced capability to handle oscillatory behaviors. Finally, the inverse discrete wavelet transform reconstructs motion sequences in the time domain, generating temporally coherent predictions. Extensive experiments on three benchmark datasets demonstrate the competitive performance of our model compared to strong baselines, as evidenced by both quantitative and qualitative evaluations. Moreover, its compact architecture coupled with the linear recurrence of Lucas polynomials, ensures computational efficiency.

AHDMIL: Asymmetric Hierarchical Distillation Multi-Instance Learning for Fast and Accurate Whole-Slide Image Classification

Authors: Jiuyang Dong, Jiahan Li, Junjun Jiang, Kui Jiang, Yongbing Zhang

Abstract: Although multi-instance learning (MIL) has succeeded in pathological image classification, it faces the challenge of high inference costs due to the need to process thousands of patches from each gigapixel whole slide image (WSI). To address this, we propose AHDMIL, an Asymmetric Hierarchical Distillation Multi-Instance Learning framework that enables fast and accurate classification by eliminating irrelevant patches through a two-step training process. AHDMIL comprises two key components: the Dynamic Multi-Instance Network (DMIN), which operates on high-resolution WSIs, and the Dual-Branch Lightweight Instance Pre-screening Network (DB-LIPN), which analyzes corresponding low-resolution counterparts. In the first step, self-distillation (SD), DMIN is trained for WSI classification while generating per-instance attention scores to identify irrelevant patches. These scores guide the second step, asymmetric distillation (AD), where DB-LIPN learns to predict the relevance of each low-resolution patch. The relevant patches predicted by DB-LIPN have spatial correspondence with patches in high-resolution WSIs, which are used for fine-tuning and efficient inference of DMIN. In addition, we design the first Chebyshev-polynomial-based Kolmogorov-Arnold (CKA) classifier in computational pathology, which improves classification performance through learnable activation layers. Extensive experiments on four public datasets demonstrate that AHDMIL consistently outperforms previous state-of-the-art methods in both classification performance and inference speed. For example, on the Camelyon16 dataset, it achieves a relative improvement of 5.3% in accuracy and accelerates inference by 1.2.times. Across all datasets, area under the curve (AUC), accuracy, f1 score, and brier score show consistent gains, with average inference speedups ranging from 1.2 to 2.1 times. The code is available.

Optimizing IoT Threat Detection with Kolmogorov-Arnold Networks (KANs)

Authors: Natalia Emelianova, Carlos Kamienski, Ronaldo C. Prati

Abstract: The exponential growth of the Internet of Things (IoT) has led to the emergence of substantial security concerns, with IoT networks becoming the primary target for cyberattacks. This study examines the potential of Kolmogorov-Arnold Networks (KANs) as an alternative to conventional machine learning models for intrusion detection in IoT networks. The study demonstrates that KANs, which employ learnable activation functions, outperform traditional MLPs and achieve competitive accuracy compared to state-of-the-art models such as Random Forest and XGBoost, while offering superior interpretability for intrusion detection in IoT networks.

An Interpretable Multi-Plane Fusion Framework With Kolmogorov-Arnold Network Guided Attention Enhancement for Alzheimer’s Disease Diagnosis

Authors: Xiaoxiao Yang, Meiliang Liu, Yunfang Xu, Zijin Li, Zhengye Si, Xinyue Yang, Zhiwen Zhao

Abstract: Alzheimer’s disease (AD) is a progressive neurodegenerative disorder that severely impairs cognitive function and quality of life. Timely intervention in AD relies heavily on early and precise diagnosis, which remains challenging due to the complex and subtle structural changes in the brain. Most existing deep learning methods focus only on a single plane of structural magnetic resonance imaging (sMRI) and struggle to accurately capture the complex and nonlinear relationships among pathological regions of the brain, thus limiting their ability to precisely identify atrophic features. To overcome these limitations, we propose an innovative framework, MPF-KANSC, which integrates multi-plane fusion (MPF) for combining features from the coronal, sagittal, and axial planes, and a Kolmogorov-Arnold Network-guided spatial-channel attention mechanism (KANSC) to more effectively learn and represent sMRI atrophy features. Specifically, the proposed model enables parallel feature extraction from multiple anatomical planes, thus capturing more comprehensive structural information. The KANSC attention mechanism further leverages a more flexible and accurate nonlinear function approximation technique, facilitating precise identification and localization of disease-related abnormalities. Experiments on the ADNI dataset confirm that the proposed MPF-KANSC achieves superior performance in AD diagnosis. Moreover, our findings provide new evidence of right-lateralized asymmetry in subcortical structural changes during AD progression, highlighting the model’s promising interpretability.

Transferring Social Network Knowledge from Multiple GNN Teachers to Kolmogorov-Arnold Networks

Authors: Yuan-Hung Chao, Chia-Hsun Lu, Chih-Ya Shen

Abstract: Graph Neural Networks (GNNs) have shown strong performance on graph-structured data, but their reliance on graph connectivity often limits scalability and efficiency. Kolmogorov-Arnold Networks (KANs), a recent architecture with learnable univariate functions, offer strong nonlinear expressiveness and efficient inference. In this work, we integrate KANs into three popular GNN architectures-GAT, SGC, and APPNP-resulting in three new models: KGAT, KSGC, and KAPPNP. We further adopt a multi-teacher knowledge amalgamation framework, where knowledge from multiple KAN-based GNNs is distilled into a graph-independent KAN student model. Experiments on benchmark datasets show that the proposed models improve node classification accuracy, and the knowledge amalgamation approach significantly boosts student model performance. Our findings highlight the potential of KANs for enhancing GNN expressiveness and for enabling efficient, graph-free inference.

Watermarking Kolmogorov-Arnold Networks for Emerging Networked Applications via Activation Perturbation

Authors: Chia-Hsun Lu, Guan-Jhih Wu, Ya-Chi Ho, Chih-Ya Shen

Abstract: With the increasing importance of protecting intellectual property in machine learning, watermarking techniques have gained significant attention. As advanced models are increasingly deployed in domains such as social network analysis, the need for robust model protection becomes even more critical. While existing watermarking methods have demonstrated effectiveness for conventional deep neural networks, they often fail to adapt to the novel architecture, Kolmogorov-Arnold Networks (KAN), which feature learnable activation functions. KAN holds strong potential for modeling complex relationships in network-structured data. However, their unique design also introduces new challenges for watermarking. Therefore, we propose a novel watermarking method, Discrete Cosine Transform-based Activation Watermarking (DCT-AW), tailored for KAN. Leveraging the learnable activation functions of KAN, our method embeds watermarks by perturbing activation outputs using discrete cosine transform, ensuring compatibility with diverse tasks and achieving task independence. Experimental results demonstrate that DCT-AW has a small impact on model performance and provides superior robustness against various watermark removal attacks, including fine-tuning, pruning, and retraining after pruning.

KARMA: Efficient Structural Defect Segmentation via Kolmogorov-Arnold Representation Learning

Authors: Md Meftahul Ferdaus, Mahdi Abdelguerfi, Elias Ioup, Steven Sloan, Kendall N. Niles, Ken Pathak

Abstract: Semantic segmentation of structural defects in civil infrastructure remains challenging due to variable defect appearances, harsh imaging conditions, and significant class imbalance. Current deep learning methods, despite their effectiveness, typically require millions of parameters, rendering them impractical for real-time inspection systems. We introduce KARMA (Kolmogorov-Arnold Representation Mapping Architecture), a highly efficient semantic segmentation framework that models complex defect patterns through compositions of one-dimensional functions rather than conventional convolutions. KARMA features three technical innovations: (1) a parameter-efficient Tiny Kolmogorov-Arnold Network (TiKAN) module leveraging low-rank factorization for KAN-based feature transformation; (2) an optimized feature pyramid structure with separable convolutions for multi-scale defect analysis; and (3) a static-dynamic prototype mechanism that enhances feature representation for imbalanced classes. Extensive experiments on benchmark infrastructure inspection datasets demonstrate that KARMA achieves competitive or superior mean IoU performance compared to state-of-the-art approaches, while using significantly fewer parameters (0.959M vs. 31.04M, a 97% reduction). Operating at 0.264 GFLOPS, KARMA maintains inference speeds suitable for real-time deployment, enabling practical automated infrastructure inspection systems without compromising accuracy. The source code can be accessed at the following URL: https://github.com/faeyelab/karma.

Stationarity Exploration for Multivariate Time Series Forecasting

Authors: Hao Liu, Chun Yang, Zhang xiaoxing, Rui Ma, Xiaobin Zhu

Abstract: Deep learning-based time series forecasting has found widespread applications. Recently, converting time series data into the frequency domain for forecasting has become popular for accurately exploring periodic patterns. However, existing methods often cannot effectively explore stationary information from complex intertwined frequency components. In this paper, we propose a simple yet effective Amplitude-Phase Reconstruct Network (APRNet) that models the inter-relationships of amplitude and phase, which prevents the amplitude and phase from being constrained by different physical quantities, thereby decoupling the distinct characteristics of signals for capturing stationary information. Specifically, we represent the multivariate time series input across sequence and channel dimensions, highlighting the correlation between amplitude and phase at multiple interaction frequencies. We propose a novel Kolmogorov-Arnold-Network-based Local Correlation (KLC) module to adaptively fit local functions using univariate functions, enabling more flexible characterization of stationary features across different amplitudes and phases. This significantly enhances the model’s capability to capture time-varying patterns. Extensive experiments demonstrate the superiority of our APRNet against the state-of-the-arts (SOTAs).

Combating Noisy Labels via Dynamic Connection Masking

Authors: Xinlei Zhang, Fan Liu, Chuanyi Zhang, Fan Cheng, Yuhui Zheng

Abstract: Noisy labels are inevitable in real-world scenarios. Due to the strong capacity of deep neural networks to memorize corrupted labels, these noisy labels can cause significant performance degradation. Existing research on mitigating the negative effects of noisy labels has mainly focused on robust loss functions and sample selection, with comparatively limited exploration of regularization in model architecture. Inspired by the sparsity regularization used in Kolmogorov-Arnold Networks (KANs), we propose a Dynamic Connection Masking (DCM) mechanism for both Multi-Layer Perceptron Networks (MLPs) and KANs to enhance the robustness of classifiers against noisy labels. The mechanism can adaptively mask less important edges during training by evaluating their information-carrying capacity. Through theoretical analysis, we demonstrate its efficiency in reducing gradient error. Our approach can be seamlessly integrated into various noise-robust training methods to build more robust deep networks, including robust loss functions, sample selection strategies, and regularization techniques. Extensive experiments on both synthetic and real-world benchmarks demonstrate that our method consistently outperforms state-of-the-art (SOTA) approaches. Furthermore, we are also the first to investigate KANs as classifiers against noisy labels, revealing their superior noise robustness over MLPs in real-world noisy scenarios. Our code will soon be publicly available.

KAN-HAR: A Human activity recognition based on Kolmogorov-Arnold Network

Author: Mohammad Alikhani

Abstract: Human Activity Recognition (HAR) plays a critical role in numerous applications, including healthcare monitoring, fitness tracking, and smart environments. Traditional deep learning (DL) approaches, while effective, often require extensive parameter tuning and may lack interpretability. In this work, we investigate the use of a single three-axis accelerometer and the Kolmogorov–Arnold Network (KAN) for HAR tasks, leveraging its ability to model complex nonlinear relationships with improved interpretability and parameter efficiency. The MotionSense dataset, containing smartphone-based motion sensor signals across various physical activities, is employed to evaluate the proposed approach. Our methodology involves preprocessing and normalization of accelerometer and gyroscope data, followed by KAN-based feature learning and classification. Experimental results demonstrate that the KAN achieves competitive or superior classification performance compared to conventional deep neural networks, while maintaining a significantly reduced parameter count. This highlights the potential of KAN architectures as an efficient and interpretable alternative for real-world HAR systems. The open-source implementation of the proposed framework is available at the Project’s GitHub Repository.

The Wrath of KAN: Enabling Fast, Accurate, and Transparent Emulation of the Global 21 cm Cosmology Signal

Authors: J. Dorigo Jones, B. Reyes, D. Rapetti, Shah Mohammad Bahauddin, J. O. Burns, D. W. Barker

Abstract: Based on the Kolmogorov-Arnold Network (KAN), we present a novel emulator of the global 21 cm cosmology signal, $\texttt{21cmKAN}$, that provides extremely fast training speed while achieving nearly equivalent accuracy to the most accurate emulator to date, $\texttt{21cmLSTM}$. The combination of enhanced speed and accuracy facilitated by $\texttt{21cmKAN}$ enables rapid and highly accurate physical parameter estimation analyses of multiple 21 cm models, which is needed to fully characterize the complex feature space across models and produce robust constraints on the early universe. Rather than using static functions to model complex relationships like traditional fully-connected neural networks do, KANs learn expressive transformations that can perform significantly better for low-dimensional physical problems. $\texttt{21cmKAN}$ predicts a given signal for two well-known models in the community in 3.7 ms on average and trains about 75 times faster than $\texttt{21cmLSTM}$, when utilizing the same typical GPU. $\texttt{21cmKAN}$ is able to achieve these speeds because of its learnable, data-driven transformations and its relatively small number of trainable parameters compared to a memory-based emulator. We show that $\texttt{21cmKAN}$ required less than 30 minutes to train and fit these simulated signals and obtain unbiased posterior distributions. We find that the transparent architecture of $\texttt{21cmKAN}$ allows us to conveniently interpret and further validate its emulation results in terms of the sensitivity of the 21 cm signal to each physical parameter. This work demonstrates the effectiveness of KANs and their ability to more quickly and accurately mimic expensive physical simulations in comparison to other types of neural networks.

Combinations of Fast Activation and Trigonometric Functions in Kolmogorov-Arnold Networks

Authors: Hoang-Thang Ta, Duy-Quy Thai, Phuong-Linh Tran-Thi

Abstract: For years, many neural networks have been developed based on the Kolmogorov-Arnold Representation Theorem (KART), which was created to address Hilbert’s 13th problem. Recently, relying on KART, Kolmogorov-Arnold Networks (KANs) have attracted attention from the research community, stimulating the use of polynomial functions such as B-splines and RBFs. However, these functions are not fully supported by GPU devices and are still considered less popular. In this paper, we propose the use of fast computational functions, such as ReLU and trigonometric functions (e.g., ReLU, sin, cos, arctan), as basis components in Kolmogorov-Arnold Networks (KANs). By integrating these function combinations into the network structure, we aim to enhance computational efficiency. Experimental results show that these combinations maintain competitive performance while offering potential improvements in training time and generalization.

Skin Cancer Classification: Hybrid CNN-Transformer Models with KAN-Based Fusion

Authors: Shubhi Agarwal, Amulya Kumar Mahto

Abstract: Skin cancer classification is a crucial task in medical image analysis, where precise differentiation between malignant and non-malignant lesions is essential for early diagnosis and treatment. In this study, we explore Sequential and Parallel Hybrid CNN-Transformer models with Convolutional Kolmogorov-Arnold Network (CKAN). Our approach integrates transfer learning and extensive data augmentation, where CNNs extract local spatial features, Transformers model global dependencies, and CKAN facilitates nonlinear feature fusion for improved representation learning. To assess generalization, we evaluate our models on multiple benchmark datasets (HAM10000,BCN20000 and PAD-UFES) under varying data distributions and class imbalances. Experimental results demonstrate that hybrid CNN-Transformer architectures effectively capture both spatial and contextual features, leading to improved classification performance. Additionally, the integration of CKAN enhances feature fusion through learnable activation functions, yielding more discriminative representations. Our proposed approach achieves competitive performance in skin cancer classification, demonstrating 92.81% accuracy and 92.47% F1-score on the HAM10000 dataset, 97.83% accuracy and 97.83% F1-score on the PAD-UFES dataset, and 91.17% accuracy with 91.79% F1- score on the BCN20000 dataset highlighting the effectiveness and generalizability of our model across diverse datasets. This study highlights the significance of feature representation and model design in advancing robust and accurate medical image classification.

Conditionally adaptive augmented Lagrangian method for physics-informed learning of forward and inverse problems

Authors: Qifeng Hu, Shamsulhaq Basir, Inanc Senocak

Abstract: We present several key advances to the Physics and Equality Constrained Artificial Neural Networks (PECANN) framework, substantially improving its capacity to solve challenging partial differential equations (PDEs). Our enhancements broaden the framework’s applicability and improve efficiency. First, we generalize the Augmented Lagrangian Method (ALM) to support multiple, independent penalty parameters for enforcing heterogeneous constraints. Second, we introduce a constraint aggregation technique to address inefficiencies associated with point-wise enforcement. Third, we incorporate a single Fourier feature mapping to capture highly oscillatory solutions with multi-scale features, where alternative methods often require multiple mappings or costlier architectures. Fourth, a novel time-windowing strategy enables seamless long-time evolution without relying on discrete time models. Fifth, and critically, we propose a conditionally adaptive penalty update (CAPU) strategy for ALM that accelerates the growth of Lagrange multipliers for constraints with larger violations, while enabling coordinated updates of multiple penalty parameters. CAPU accelerates the growth of Lagrange multipliers for selectively challenging constraints, enhancing constraint enforcement during training. We demonstrate the effectiveness of PECANN-CAPU across diverse problems, including the transonic rarefaction problem, reversible scalar advection by a vortex, high-wavenumber Helmholtz and Poisson’s equations, and inverse heat source identification. The framework achieves competitive accuracy across all cases when compared with established methods and recent approaches based on Kolmogorov-Arnold networks. Collectively, these advances improve the robustness, computational efficiency, and applicability of PECANN to demanding problems in scientific computing.

Physics-Informed Kolmogorov-Arnold Networks for multi-material elasticity problems in electronic packaging

Authors: Yanpeng Gong, Yida He, Yue Mei, Xiaoying Zhuang, Fei Qin, Timon Rabczuk

Abstract: This paper proposes a Physics-Informed Kolmogorov-Arnold Network for analyzing elasticity problems in multi-material electronic packaging structures. The method replaces traditional Multi-Layer Perceptrons with Kolmogorov-Arnold Networks within an energy-based Physics-Informed Neural Network framework. By constructing admissible displacement fields satisfying essential boundary conditions and optimizing network parameters through numerical integration, the proposed method effectively handles material property discontinuities. Unlike traditional methods that require domain decomposition and interface constraints for multi-material problems, Kolmogorov-Arnold Networks’ trainable B-spline activation functions provide inherent piecewise characteristics. This capability stems from B-splines’ local support, which enables effective approximation of discontinuities despite their individual smoothness. Consequently, this approach enables accurate approximation across the entire domain using a single network and simplifying the computational framework. Numerical experiments demonstrate that the proposed method achieves excellent accuracy and robustness in multi-material elasticity problems, validating its practical potential for electronic packaging analysis. Source codes are available at https://github.com/yanpeng-gong/PIKAN-MultiMaterial.

Optimizing Neural Networks with Learnable Non-Linear Activation Functions via Lookup-Based FPGA Acceleration

Authors: Mengyuan Yin, Benjamin Chen Ming Choong, Chuping Qu, Rick Siow Mong Goh, Weng-Fai Wong, Tao Luo

Abstract: Learned activation functions in models like Kolmogorov-Arnold Networks (KANs) outperform fixed-activation architectures in terms of accuracy and interpretability; however, their computational complexity poses critical challenges for energy-constrained edge AI deployments. Conventional CPUs/GPUs incur prohibitive latency and power costs when evaluating higher order activations, limiting deployability under ultra-tight energy budgets. We address this via a reconfigurable lookup architecture with edge FPGAs. By coupling fine-grained quantization with adaptive lookup tables, our design minimizes energy-intensive arithmetic operations while preserving activation fidelity. FPGA reconfigurability enables dynamic hardware specialization for learned functions, a key advantage for edge systems that require post-deployment adaptability. Evaluations using KANs - where unique activation functions play a critical role - demonstrate that our FPGA-based design achieves superior computational speed and over $10^4$ times higher energy efficiency compared to edge CPUs and GPUs, while maintaining matching accuracy and minimal footprint overhead. This breakthrough positions our approach as a practical enabler for energy-critical edge AI, where computational intensity and power constraints traditionally preclude the use of adaptive activation networks.

E-BayesSAM: Efficient Bayesian Adaptation of SAM with Self-Optimizing KAN-Based Interpretation for Uncertainty-Aware Ultrasonic Segmentation

Authors: Bin Huang, Zhong Liu, Huiying Wen, Bingsheng Huang, Xin Chen, Shuo Li

Abstract: Although the Segment Anything Model (SAM) has advanced medical image segmentation, its Bayesian adaptation for uncertainty-aware segmentation remains hindered by three key issues: (1) instability in Bayesian fine-tuning of large pre-trained SAMs; (2) high computation cost due to SAM’s massive parameters; (3) SAM’s black-box design limits interpretability. To overcome these, we propose E-BayesSAM, an efficient framework combining Token-wise Variational Bayesian Inference (T-VBI) for efficienty Bayesian adaptation and Self-Optimizing Kolmogorov-Arnold Network (SO-KAN) for improving interpretability. T-VBI innovatively reinterprets SAM’s output tokens as dynamic probabilistic weights and reparameterizes them as latent variables without auxiliary training, enabling training-free VBI for uncertainty estimation. SO-KAN improves token prediction with learnable spline activations via self-supervised learning, providing insight to prune redundant tokens to boost efficiency and accuracy. Experiments on five ultrasound datasets demonstrated that E-BayesSAM achieves: (i) real-time inference (0.03s/image), (ii) superior segmentation accuracy (average DSC: Pruned E-BayesSAM’s 89.0\% vs. E-BayesSAM’s 88.0% vs. MedSAM’s 88.3%), and (iii) identification of four critical tokens governing SAM’s decisions. By unifying efficiency, reliability, and interpretability, E-BayesSAM bridges SAM’s versatility with clinical needs, advancing deployment in safety-critical medical applications. The source code is available at https://github.com/mp31192/E-BayesSAM.

Programmable k-local Ising Machines and all-optical Kolmogorov-Arnold Networks on Photonic Platforms

Authors: Nikita Stroev, Natalia G. Berloff

Abstract: Photonic computing promises energy-efficient acceleration for optimization and learning, yet discrete combinatorial search and continuous function approximation have largely required distinct devices and control stacks. Here we unify k-local Ising optimization and optical Kolmogorov-Arnold network (KAN) learning on a single photonic platform, establishing a critical convergence point in optical computing. We introduce an SLM-centric primitive that realizes, in one stroke, all-optical k-local Ising interactions and fully optical KAN layers. The key idea is to convert the structural nonlinearity of a nominally linear scatterer into a per-window computational resource by adding a single relay pass through the same spatial light modulator: a folded 4f relay re-images the first Fourier plane onto the SLM so that each selected clique or channel occupies a disjoint window with its own second pass phase patch. Propagation remains linear in the optical field, yet the measured intensity in each window becomes a freely programmable polynomial of the clique sum or projection amplitude. This yields native, per clique k-local couplings without nonlinear media and, in parallel, the many independent univariate nonlinearities required by KAN layers, all trainable with in-situ physical gradients using two frames (forward and adjoint). We outline implementations on spatial photonic Ising machines, injection-locked vertical cavity surface emitting laser (VCSEL) arrays, and Microsoft analog optical computers; in all cases the hardware change is one extra lens and a fold (or an on-chip 4f loop), enabling a minimal overhead, massively parallel route to high-order Ising optimization and trainable, all-optical KAN processing on one platform.

Unveiling the Actual Performance of Neural-based Models for Equation Discovery on Graph Dynamical Systems

Authors: Riccardo Cappi, Paolo Frazzetto, Nicolò Navarin, Alessandro Sperduti

Abstract: The ``black-box’’ nature of deep learning models presents a significant barrier to their adoption for scientific discovery, where interpretability is paramount. This challenge is especially pronounced in discovering the governing equations of dynamical processes on networks or graphs, since even their topological structure further affects the processes’ behavior. This paper provides a rigorous, comparative assessment of state-of-the-art symbolic regression techniques for this task. We evaluate established methods, including sparse regression and MLP-based architectures, and introduce a novel adaptation of Kolmogorov-Arnold Networks (KANs) for graphs, designed to exploit their inherent interpretability. Across a suite of synthetic and real-world dynamical systems, our results demonstrate that both MLP and KAN-based architectures can successfully identify the underlying symbolic equations, significantly surpassing existing baselines. Critically, we show that KANs achieve this performance with greater parsimony and transparency, as their learnable activation functions provide a clearer mapping to the true physical dynamics. This study offers a practical guide for researchers, clarifying the trade-offs between model expressivity and interpretability, and establishes the viability of neural-based architectures for robust scientific discovery on complex systems.

Lightweight posterior construction for gravitational-wave catalogs with the Kolmogorov-Arnold network

Authors: Wenshuai Liu, Yiming Dong, Ziming Wang, Lijing Shao

Abstract: Neural density estimation has seen widespread applications in the gravitational-wave (GW) data analysis, which enables real-time parameter estimation for compact binary coalescences and enhances rapid inference for subsequent analysis such as population inference. In this work, we explore the application of using the Kolmogorov-Arnold network (KAN) to construct efficient and interpretable neural density estimators for lightweight posterior construction of GW catalogs. By replacing conventional activation functions with learnable splines, KAN achieves superior interpretability, higher accuracy, and greater parameter efficiency on related scientific tasks. Leveraging this feature, we propose a KAN-based neural density estimator, which ingests megabyte-scale GW posterior samples and compresses them into model weights of tens of kilobytes. Subsequently, analytic expressions requiring only several kilobytes can be further distilled from these neural network weights with minimal accuracy trade-off. In practice, GW posterior samples with fidelity can be regenerated rapidly using the model weights or analytic expressions for subsequent analysis. Our lightweight posterior construction strategy is expected to facilitate user-level data storage and transmission, paving a path for efficient analysis of numerous GW events in the next-generation GW detectors.

QuadKAN: KAN-Enhanced Quadruped Motion Control via End-to-End Reinforcement Learning

Authors: Yinuo Wang, Gavin Tao

Abstract: We address vision-guided quadruped motion control with reinforcement learning (RL) and highlight the necessity of combining proprioception with vision for robust control. We propose QuadKAN, a spline-parameterized cross-modal policy instantiated with Kolmogorov-Arnold Networks (KANs). The framework incorporates a spline encoder for proprioception and a spline fusion head for proprioception-vision inputs. This structured function class aligns the state-to-action mapping with the piecewise-smooth nature of gait, improving sample efficiency, reducing action jitter and energy consumption, and providing interpretable posture-action sensitivities. We adopt Multi-Modal Delay Randomization (MMDR) and perform end-to-end training with Proximal Policy Optimization (PPO). Evaluations across diverse terrains, including both even and uneven surfaces and scenarios with static or dynamic obstacles, demonstrate that QuadKAN achieves consistently higher returns, greater distances, and fewer collisions than state-of-the-art (SOTA) baselines. These results show that spline-parameterized policies offer a simple, effective, and interpretable alternative for robust vision-guided locomotion. A repository will be made available upon acceptance.

Kolmogorov-Arnold Representation for Symplectic Learning: Advancing Hamiltonian Neural Networks

Authors: Zongyu Wu, Ruichen Xu, Luoyao Chen, Georgios Kementzidis, Siyao Wang, Yuefan Deng

Abstract: We propose a Kolmogorov-Arnold Representation-based Hamiltonian Neural Network (KAR-HNN) that replaces the Multilayer Perceptrons (MLPs) with univariate transformations. While Hamiltonian Neural Networks (HNNs) ensure energy conservation by learning Hamiltonian functions directly from data, existing implementations, often relying on MLPs, cause hypersensitivity to the hyperparameters while exploring complex energy landscapes. Our approach exploits the localized function approximations to better capture high-frequency and multi-scale dynamics, reducing energy drift and improving long-term predictive stability. The networks preserve the symplectic form of Hamiltonian systems, and thus maintain interpretability and physical consistency. After assessing KAR-HNN on four benchmark problems including spring-mass, simple pendulum, two- and three-body problem, we foresee its effectiveness for accurate and stable modeling of realistic physical processes often at high dimensions and with few known parameters.

Symbolic Equation Modeling of Composite Loads: A Kolmogorov-Arnold Network based Learning Approach

Authors: Sonam Dorji, Yongkang Sun, Yuchen Zhang, Ghavameddin Nourbakhsh, Yateendra Mishra, Yan Xu

Abstract: With increasing penetration of distributed energy resources installed behind the meter, there is a growing need for adequate modelling of composite loads to enable accurate power system simulation analysis. Existing measurement based load modeling methods either fit fixed-structure physical models, which limits adaptability to evolving load mixes, or employ flexible machine learning methods which are however black boxes and offer limited interpretability. This paper presents a new learning based load modelling method based on Kolmogorov Arnold Networks towards modelling flexibility and interpretability. By actively learning activation functions on edges, KANs automatically derive free form symbolic equations that capture nonlinear relationships among measured variables without prior assumptions about load structure. Case studies demonstrate that the proposed approach outperforms other methods in both accuracy and generalization ability, while uniquely representing composite loads into transparent, interpretable mathematical equations.

Fractal Flow: Hierarchical and Interpretable Normalizing Flow via Topic Modeling and Recursive Strategy

Authors: Binhui Zhang, Jianwei Ma

Abstract: Normalizing Flows provide a principled framework for high-dimensional density estimation and generative modeling by constructing invertible transformations with tractable Jacobian determinants. We propose Fractal Flow, a novel normalizing flow architecture that enhances both expressiveness and interpretability through two key innovations. First, we integrate Kolmogorov-Arnold Networks and incorporate Latent Dirichlet Allocation into normalizing flows to construct a structured, interpretable latent space and model hierarchical semantic clusters. Second, inspired by Fractal Generative Models, we introduce a recursive modular design into normalizing flows to improve transformation interpretability and estimation accuracy. Experiments on MNIST, FashionMNIST, CIFAR-10, and geophysical data demonstrate that the Fractal Flow achieves latent clustering, controllable generation, and superior estimation accuracy.

September

Applying Deep Learning to Anomaly Detection of Russian Satellite Activity for Indications Prior to Military Activity

Authors: David Kurtenbach, Megan Manly, Zach Metzinger

Abstract: We apply deep learning techniques for anomaly detection to analyze activity of Russian-owned resident space objects (RSO) prior to the Ukraine invasion and assess the results for any findings that can be used as indications and warnings (I&W) of aggressive military behavior for future conflicts. Through analysis of anomalous activity, an understanding of possible tactics and procedures can be established to assess the existence of statistically significant changes in Russian RSO pattern of life/pattern of behavior (PoL/PoB) using publicly available two-line element (TLE) data. This research looks at statistical and deep learning approaches to assess anomalous activity. The deep learning methods assessed are isolation forest (IF), traditional autoencoder (AE), variational autoencoder (VAE), Kolmogorov Arnold Network (KAN), and a novel anchor-loss based autoencoder (Anchor AE). Each model is used to establish a baseline of on-orbit activity based on a five-year data sample. The primary investigation period focuses on the six months leading up to the invasion date of February 24, 2022. Additional analysis looks at RSO activity during an active combat period by sampling TLE data after the invasion date. The deep learning autoencoder models identify anomalies based on reconstruction errors that surpass a threshold sigma. To capture the nuance and unique characteristics of each RSO an individual model was trained for each observed space object. The research made an effort to prioritize explainability and interpretability of the model results thus each observation was assessed for anomalous behavior of the individual six orbital elements versus analyzing the input data as a single monolithic observation. The results demonstrate not only statistically significant anomalies of Russian RSO activity but also details anomalous findings to the individual orbital element.

Efficient Graph Knowledge Distillation from GNNs to Kolmogorov–Arnold Networks via Self-Attention Dynamic Sampling

Authors: Can Cui, Zilong Fu, Penghe Huang, Yuanyuan Li, Wu Deng, Dongyan Li

Abstract: Recent success of graph neural networks (GNNs) in modeling complex graph-structured data has fueled interest in deploying them on resource-constrained edge devices. However, their substantial computational and memory demands present ongoing challenges. Knowledge distillation (KD) from GNNs to MLPs offers a lightweight alternative, but MLPs remain limited by fixed activations and the absence of neighborhood aggregation, constraining distilled performance. To tackle these intertwined limitations, we propose SA-DSD, a novel self-attention-guided dynamic sampling distillation framework. To the best of our knowledge, this is the first work to employ an enhanced Kolmogorov-Arnold Network (KAN) as the student model. We improve Fourier KAN (FR-KAN+) with learnable frequency bases, phase shifts, and optimized algorithms, substantially improving nonlinear fitting capability over MLPs while preserving low computational complexity. To explicitly compensate for the absence of neighborhood aggregation that is inherent to both MLPs and KAN-based students, SA-DSD leverages a self-attention mechanism to dynamically identify influential nodes, construct adaptive sampling probability matrices, and enforce teacher-student prediction consistency. Extensive experiments on six real world datasets demonstrate that, under inductive and most of transductive settings, SA-DSD surpasses three GNN teachers by 3.05%-3.62% and improves FR-KAN+ by 15.61%. Moreover, it achieves a 16.69x parameter reduction and a 55.75% decrease in average runtime per epoch compared to key benchmarks.

Emulating Global 21 cm Cosmology Observations from the Lunar Far Side to Achieve Quick and Reliable Physical Constraints

Authors: J. Dorigo Jones, J. O. Burns, D. Rapetti, Shah Mohammad Bahauddin, B. Reyes, D. W. Barker

Abstract: Efforts are underway to measure the global 21 cm signal from neutral hydrogen, which is a powerful probe of the early universe, using NASA radio telescopes on the far side of the Moon. Physics-based models of the signal are computationally expensive to perform Bayesian multi-parameter inferences, for which we have developed novel, publicly-available neural network emulators utilizing a Long Short-Term Memory (LSTM) network and a Kolmogorov-Arnold Network (KAN). $\texttt{21cmLSTM}$ is currently the most accurate emulator in the community by leveraging the signal’s temporally-correlated structure, and $\texttt{21cmKAN}$ maintains similar accuracy while training 75 times faster, by learning expressive functional transformations. Each emulator can fit realistic mock signals and obtain unbiased physical parameter constraints, with $\texttt{21cmKAN}$ able to complete end-to-end training and inference in under 30 minutes. The implementation of machine learning tools like these in data analysis pipelines is important to fully exploit upcoming measurements of the cosmological 21 cm signal.

Toward a robust lesion detection model in breast DCE-MRI: adapting foundation models to high-risk women

Authors: Gabriel A. B. do Nascimento, Vincent Dong, Guilherme J. Cavalcante, Alex Nguyen, Thaís G. do Rêgo, Yuri Malheiros, Telmo M. Silva Filho, Carla R. Zeballos Torrez, James C. Gee, Anne Marie McCarthy, Andrew D. A. Maidment, Bruno Barufaldi

Abstract: Accurate breast MRI lesion detection is critical for early cancer diagnosis, especially in high-risk populations. We present a classification pipeline that adapts a pretrained foundation model, the Medical Slice Transformer (MST), for breast lesion classification using dynamic contrast-enhanced MRI (DCE-MRI). Leveraging DINOv2-based self-supervised pretraining, MST generates robust per-slice feature embeddings, which are then used to train a Kolmogorov–Arnold Network (KAN) classifier. The KAN provides a flexible and interpretable alternative to conventional convolutional networks by enabling localized nonlinear transformations via adaptive B-spline activations. This enhances the model’s ability to differentiate benign from malignant lesions in imbalanced and heterogeneous clinical datasets. Experimental results demonstrate that the MST+KAN pipeline outperforms the baseline MST classifier, achieving AUC = 0.80 \pm 0.02 while preserving interpretability through attention-based heatmaps. Our findings highlight the effectiveness of combining foundation model embeddings with advanced classification strategies for building robust and generalizable breast MRI analysis tools.

AR-KAN: Autoregressive-Weight-Enhanced Kolmogorov-Arnold Network for Time Series Forecasting

Authors: Chen Zeng, Tiehang Xu, Qiao Wang

Abstract: Traditional neural networks struggle to capture the spectral structure of complex signals. Fourier neural networks (FNNs) attempt to address this by embedding Fourier series components, yet many real-world signals are almost-periodic with non-commensurate frequencies, posing additional challenges. Building on prior work showing that ARIMA outperforms large language models (LLMs) for time series forecasting, we extend the comparison to neural predictors and find that ARIMA still maintains a clear advantage. Inspired by this finding, we propose the Autoregressive-Weight-Enhanced Kolmogorov-Arnold Network (AR-KAN). Based in the Universal Myopic Mapping Theorem, it integrates a pre-trained AR module for temporal memory with a KAN for nonlinear representation. We prove that the AR module preserves essential temporal features while reducing redundancy, and that the upper bound of the approximation error for AR-KAN is smaller than that for KAN in a probabilistic sense. Experimental results also demonstrate that AR-KAN delivers exceptional performance compared to existing models, both on synthetic almost-periodic functions and real-world datasets. These results highlight AR-KAN as a robust and effective framework for time series forecasting. Our code is available at https://github.com/ChenZeng001/AR-KAN.

Initialization Schemes for Kolmogorov-Arnold Networks: An Empirical Study

Authors: Spyros Rigas, Dhruv Verma, Georgios Alexandridis, Yixuan Wang

Abstract: Kolmogorov-Arnold Networks (KANs) are a recently introduced neural architecture that replace fixed nonlinearities with trainable activation functions, offering enhanced flexibility and interpretability. While KANs have been applied successfully across scientific and machine learning tasks, their initialization strategies remain largely unexplored. In this work, we study initialization schemes for spline-based KANs, proposing two theory-driven approaches inspired by LeCun and Glorot, as well as an empirical power-law family with tunable exponents. Our evaluation combines large-scale grid searches on function fitting and forward PDE benchmarks, an analysis of training dynamics through the lens of the Neural Tangent Kernel, and evaluations on a subset of the Feynman dataset. Our findings indicate that the Glorot-inspired initialization significantly outperforms the baseline in parameter-rich models, while power-law initialization achieves the strongest performance overall, both across tasks and for architectures of varying size. All code and data accompanying this manuscript are publicly available at https://github.com/srigas/KAN_Initialization_Schemes.

A Kolmogorov-Arnold Network for Interpretable Cyberattack Detection in AGC Systems

Authors: Jehad Jilan, Niranjana Naveen Nambiar, Ahmad Mohammad Saber, Alok Paranjape, Amr Youssef, Deepa Kundur

Abstract: Automatic Generation Control (AGC) is essential for power grid stability but remains vulnerable to stealthy cyberattacks, such as False Data Injection Attacks (FDIAs), which can disturb the system’s stability while evading traditional detection methods. Unlike previous works that relied on blackbox approaches, this work proposes Kolmogorov-Arnold Networks (KAN) as an interpretable and accurate method for FDIA detection in AGC systems, considering the system nonlinearities. KAN models include a method for extracting symbolic equations, and are thus able to provide more interpretability than the majority of machine learning models. The proposed KAN is trained offline to learn the complex nonlinear relationships between the AGC measurements under different operating scenarios. After training, symbolic formulas that describe the trained model’s behavior can be extracted and leveraged, greatly enhancing interpretability. Our findings confirm that the proposed KAN model achieves FDIA detection rates of up to 95.97% and 95.9% for the initial model and the symbolic formula, respectively, with a low false alarm rate, offering a reliable approach to enhancing AGC cybersecurity.

Hardware Acceleration of Kolmogorov-Arnold Network (KAN) in Large-Scale Systems

Authors: Wei-Hsing Huang, Jianwei Jia, Yuyao Kong, Faaiq Waqar, Tai-Hao Wen, Meng-Fan Chang, Shimeng Yu

Abstract: Recent developments have introduced Kolmogorov-Arnold Networks (KAN), an innovative architectural paradigm capable of replicating conventional deep neural network (DNN) capabilities while utilizing significantly reduced parameter counts through the employment of parameterized B-spline functions with trainable coefficients. Nevertheless, the B-spline functional components inherent to KAN architectures introduce distinct hardware acceleration complexities. While B-spline function evaluation can be accomplished through look-up table (LUT) implementations that directly encode functional mappings, thus minimizing computational overhead, such approaches continue to demand considerable circuit infrastructure, including LUTs, multiplexers, decoders, and related components. This work presents an algorithm-hardware co-design approach for KAN acceleration. At the algorithmic level, techniques include Alignment-Symmetry and PowerGap KAN hardware aware quantization, KAN sparsity aware mapping strategy, and circuit-level techniques include N:1 Time Modulation Dynamic Voltage input generator with analog-compute-in-memory (ACIM) circuits. This work conducts evaluations on large-scale KAN networks to validate the proposed methodologies. Non-ideality factors, including partial sum deviations from process variations, have been evaluated with statistics measured from the TSMC 22nm RRAM-ACIM prototype chips. Utilizing optimally determined KAN hyperparameters in conjunction with circuit optimizations fabricated at the 22nm technology node, despite the parameter count for large-scale tasks in this work increasing by 500Kx to 807Kx compared to tiny-scale tasks in previous work, the area overhead increases by only 28Kx to 41Kx, with power consumption rising by merely 51x to 94x, while accuracy degradation remains minimal at 0.11% to 0.23%, demonstrating the scaling potential of our proposed architecture.

An Interpretable AI Framework to Disentangle Self-Interacting and Cold Dark Matter in Galaxy Clusters: The CKAN Approach

Authors: Zhenyang Huang, Haihao Shi, Zhiyong Liu, Na Wang

Abstract: Convolutional neural networks have shown their ability to differentiate between self-interacting dark matter (SIDM) and cold dark matter (CDM) on galaxy cluster scales. However, their large parameter counts and ‘‘black-box’’ nature make it difficult to assess whether their decisions adhere to physical principles. To address this issue, we have built a Convolutional Kolmogorov-Arnold Network (CKAN) that reduces parameter count and enhances interpretability, and propose a novel analytical framework to understand the network’s decision-making process. With this framework, we leverage our network to qualitatively assess the offset between the dark matter distribution center and the galaxy cluster center, as well as the size of heating regions in different models. These findings are consistent with current theoretical predictions and show the reliability and interpretability of our network. By combining network interpretability with unseen test results, we also estimate that for SIDM in galaxy clusters, the minimum cross-section $(σ/m)_{\mathrm{th}}$ required to reliably identify its collisional nature falls between $0.1\,\mathrm{cm}^2/\mathrm{g}$ and $0.3\,\mathrm{cm}^2/\mathrm{g}$. Moreover, CKAN maintains robust performance under simulated JWST and Euclid noise, highlighting its promise for application to forthcoming observational surveys.

Lookup multivariate Kolmogorov-Arnold Networks

Authors: Sergey Pozdnyakov, Philippe Schwaller

Abstract: High-dimensional linear mappings, or linear layers, dominate both the parameter count and the computational cost of most modern deep-learning models. We introduce a general-purpose drop-in replacement, lookup multivariate Kolmogorov-Arnold Networks (lmKANs), which deliver a substantially better trade-off between capacity and inference cost. Our construction expresses a general high-dimensional mapping through trainable low-dimensional multivariate functions. These functions can carry dozens or hundreds of trainable parameters each, and yet it takes only a few multiplications to compute them because they are implemented as spline lookup tables. Empirically, lmKANs reduce inference FLOPs by up to 6.0x while matching the flexibility of MLPs in general high-dimensional function approximation. In another feedforward fully connected benchmark, on the tabular-like dataset of randomly displaced methane configurations, lmKANs enable more than 10x higher H100 throughput at equal accuracy. Within frameworks of Convolutional Neural Networks, lmKAN-based CNNs cut inference FLOPs at matched accuracy by 1.6-2.1x and by 1.7x on the CIFAR-10 and ImageNet-1k datasets, respectively. Our code, including dedicated CUDA kernels, is available online at https://github.com/schwallergroup/lmkan.

KAN-Therm: A Lightweight Battery Thermal Model Using Kolmogorov-Arnold Network

Authors: Soumyoraj Mallick, Faysal Ahamed, Sanchita Ghosh, Tanushree Roy

Abstract: A battery management system (BMS) relies on real-time estimation of battery temperature distribution in battery cells to ensure safe and optimal operation of Lithium-ion batteries. However, physical BMS often suffers from memory and computational resource limitations required by high-fidelity models. Temperature estimation of batteries for safety-critical systems using physics-based models on physical BMS can potentially become challenging due to their higher computational time. In contrast, neural network-based approaches offer faster estimation but require greater memory overhead. To address these challenges, we propose Kolmogorov-Arnold network (KAN) based thermal model, KAN-therm, to estimate the core temperature of a cylindrical battery. Unlike traditional neural network architectures, KAN uses learnable nonlinear activation functions that can effectively capture system complexity using relatively lean models. We have compared the memory overhead and estimation time of our model with state-of-the-art neural network and tree-based models to demonstrate the applicability and potential scalability of KAN-therm on a physical BMS.

KAN-SR: A Kolmogorov-Arnold Network Guided Symbolic Regression Framework

Authors: Marco Andrea Bühler, Gonzalo Guillén-Gosálbez

Abstract: We introduce a novel symbolic regression framework, namely KAN-SR, built on Kolmogorov Arnold Networks (KANs) which follows a divide-and-conquer approach. Symbolic regression searches for mathematical equations that best fit a given dataset and is commonly solved with genetic programming approaches. We show that by using deep learning techniques, more specific KANs, and combining them with simplification strategies such as translational symmetries and separabilities, we are able to recover ground-truth equations of the Feynman Symbolic Regression for Scientific Discovery (SRSD) dataset. Additionally, we show that by combining the proposed framework with neural controlled differential equations, we are able to model the dynamics of an in-silico bioprocess system precisely, opening the door for the dynamic modeling of other engineering systems.

SOH-KLSTM: A Hybrid Kolmogorov-Arnold Network and LSTM Model for Enhanced Lithium-Ion Battery Health Monitoring

Authors: Imen Jarraya, Safa Ben Atitallah, Fatimah Alahmeda, Mohamed Abdelkadera, Maha Drissa, Fatma Abdelhadic, Anis Koubaaa

Abstract: Accurate and reliable State Of Health (SOH) estimation for Lithium (Li) batteries is critical to ensure the longevity, safety, and optimal performance of applications like electric vehicles, unmanned aerial vehicles, consumer electronics, and renewable energy storage systems. Conventional SOH estimation techniques fail to represent the non-linear and temporal aspects of battery degradation effectively. In this study, we propose a novel SOH prediction framework (SOH-KLSTM) using Kolmogorov-Arnold Network (KAN)-Integrated Candidate Cell State in LSTM for Li batteries Health Monitoring. This hybrid approach combines the ability of LSTM to learn long-term dependencies for accurate time series predictions with KAN’s non-linear approximation capabilities to effectively capture complex degradation behaviors in Lithium batteries.

Task-Agnostic Learnable Weighted-Knowledge Base Scheme for Robust Semantic Communications

Authors: Shiyao Jiang, Jian Jiao, Xingjian Zhang, Ye Wang, Dusit Niyato, Qinyu Zhang

Abstract: With the emergence of diverse and massive data in the upcoming sixth-generation (6G) networks, the task-agnostic semantic communication system is regarded to provide robust intelligent services. In this paper, we propose a task-agnostic learnable weighted-knowledge base semantic communication (TALSC) framework for robust image transmission to address the real-world heterogeneous data bias in KB, including label flipping noise and class imbalance. The TALSC framework incorporates a sample confidence module (SCM) as meta-learner and the semantic coding networks as learners. The learners are updated based on the empirical knowledge provided by the learnable weighted-KB (LW-KB). Meanwhile, the meta-learner evaluates the significance of samples according to the task loss feedback, and adjusts the update strategy of learners to enhance the robustness in semantic recovery for unknown tasks. To strike a balance between SCM parameters and precision of significance evaluation, we design an SCM-grid extension (SCM-GE) approach by embedding the Kolmogorov-Arnold networks (KAN) within SCM, which leverages the concept of spline refinement in KAN and enables scalable SCM with customizable granularity without retraining. Simulations demonstrate that the TALSC framework effectively mitigates the effects of flipping noise and class imbalance in task-agnostic image semantic communication, achieving at least 12% higher semantic recovery accuracy (SRA) and multi-scale structural similarity (MS-SSIM) compared to state-of-the-art methods.

Multimodal Regression for Enzyme Turnover Rates Prediction

Authors: Bozhen Hu, Cheng Tan, Siyuan Li, Jiangbin Zheng, Sizhe Qiu, Jun Xia, Stan Z. Li

Abstract: The enzyme turnover rate is a fundamental parameter in enzyme kinetics, reflecting the catalytic efficiency of enzymes. However, enzyme turnover rates remain scarce across most organisms due to the high cost and complexity of experimental measurements. To address this gap, we propose a multimodal framework for predicting the enzyme turnover rate by integrating enzyme sequences, substrate structures, and environmental factors. Our model combines a pre-trained language model and a convolutional neural network to extract features from protein sequences, while a graph neural network captures informative representations from substrate molecules. An attention mechanism is incorporated to enhance interactions between enzyme and substrate representations. Furthermore, we leverage symbolic regression via Kolmogorov-Arnold Networks to explicitly learn mathematical formulas that govern the enzyme turnover rate, enabling interpretable and accurate predictions. Extensive experiments demonstrate that our framework outperforms both traditional and state-of-the-art deep learning approaches. This work provides a robust tool for studying enzyme kinetics and holds promise for applications in enzyme engineering, biotechnology, and industrial biocatalysis.

Spontaneous Kolmogorov-Arnold Geometry in Shallow MLPs

Authors: Michael H. Freedman, Michael Mulligan

Abstract: The Kolmogorov-Arnold (KA) representation theorem constructs universal, but highly non-smooth inner functions (the first layer map) in a single (non-linear) hidden layer neural network. Such universal functions have a distinctive local geometry, a “texture,” which can be characterized by the inner function’s Jacobian $J({\mathbf{x}})$, as $\mathbf{x}$ varies over the data. It is natural to ask if this distinctive KA geometry emerges through conventional neural network optimization. We find that indeed KA geometry often is produced when training vanilla single hidden layer neural networks. We quantify KA geometry through the statistical properties of the exterior powers of $J(\mathbf{x})$: number of zero rows and various observables for the minor statistics of $J(\mathbf{x})$, which measure the scale and axis alignment of $J(\mathbf{x})$. This leads to a rough understanding for where KA geometry occurs in the space of function complexity and model hyperparameters. The motivation is first to understand how neural networks organically learn to prepare input data for later downstream processing and, second, to learn enough about the emergence of KA geometry to accelerate learning through a timely intervention in network hyperparameters. This research is the “flip side” of KA-Networks (KANs). We do not engineer KA into the neural network, but rather watch KA emerge in shallow MLPs.

FunKAN: Functional Kolmogorov-Arnold Network for Medical Image Enhancement and Segmentation

Authors: Maksim Penkin, Andrey Krylov

Abstract: Medical image enhancement and segmentation are critical yet challenging tasks in modern clinical practice, constrained by artifacts and complex anatomical variations. Traditional deep learning approaches often rely on complex architectures with limited interpretability. While Kolmogorov-Arnold networks offer interpretable solutions, their reliance on flattened feature representations fundamentally disrupts the intrinsic spatial structure of imaging data. To address this issue we propose a Functional Kolmogorov-Arnold Network (FunKAN) – a novel interpretable neural framework, designed specifically for image processing, that formally generalizes the Kolmogorov-Arnold representation theorem onto functional spaces and learns inner functions using Fourier decomposition over the basis Hermite functions. We explore FunKAN on several medical image processing tasks, including Gibbs ringing suppression in magnetic resonance images, benchmarking on IXI dataset. We also propose U-FunKAN as state-of-the-art binary medical segmentation model with benchmarks on three medical datasets: BUSI (ultrasound images), GlaS (histological structures) and CVC-ClinicDB (colonoscopy videos), detecting breast cancer, glands and polyps, respectively. Experiments on those diverse datasets demonstrate that our approach outperforms other KAN-based backbones in both medical image enhancement (PSNR, TV) and segmentation (IoU, F1). Our work bridges the gap between theoretical function approximation and medical image analysis, offering a robust, interpretable solution for clinical applications.

Taylor-Series Expanded Kolmogorov-Arnold Network for Medical Imaging Classification

Authors: Kaniz Fatema, Emad A. Mohammed, Sukhjit Singh Sehra

Abstract: Effective and interpretable classification of medical images is a challenge in computer-aided diagnosis, especially in resource-limited clinical settings. This study introduces spline-based Kolmogorov-Arnold Networks (KANs) for accurate medical image classification with limited, diverse datasets. The models include SBTAYLOR-KAN, integrating B-splines with Taylor series; SBRBF-KAN, combining B-splines with Radial Basis Functions; and SBWAVELET-KAN, embedding B-splines in Morlet wavelet transforms. These approaches leverage spline-based function approximation to capture both local and global nonlinearities. The models were evaluated on brain MRI, chest X-rays, tuberculosis X-rays, and skin lesion images without preprocessing, demonstrating the ability to learn directly from raw data. Extensive experiments, including cross-dataset validation and data reduction analysis, showed strong generalization and stability. SBTAYLOR-KAN achieved up to 98.93% accuracy, with a balanced F1-score, maintaining over 86% accuracy using only 30% of the training data across three datasets. Despite class imbalance in the skin cancer dataset, experiments on both imbalanced and balanced versions showed SBTAYLOR-KAN outperforming other models, achieving 68.22% accuracy. Unlike traditional CNNs, which require millions of parameters (e.g., ResNet50 with 24.18M), SBTAYLOR-KAN achieves comparable performance with just 2,872 trainable parameters, making it more suitable for constrained medical environments. Gradient-weighted Class Activation Mapping (Grad-CAM) was used for interpretability, highlighting relevant regions in medical images. This framework provides a lightweight, interpretable, and generalizable solution for medical image classification, addressing the challenges of limited datasets and data-scarce scenarios in clinical AI applications.

Quantum Variational Activation Functions Empower Kolmogorov-Arnold Networks

Authors: Jiun-Cheng Jiang, Morris Yu-Chao Huang, Tianlong Chen, Hsi-Sheng Goan

Abstract: Variational quantum circuits (VQCs) are central to quantum machine learning, while recent progress in Kolmogorov-Arnold networks (KANs) highlights the power of learnable activation functions. We unify these directions by introducing quantum variational activation functions (QVAFs), realized through single-qubit data re-uploading circuits called DatA Re-Uploading ActivatioNs (DARUANs). We show that DARUAN with trainable weights in data pre-processing possesses an exponentially growing frequency spectrum with data repetitions, enabling an exponential reduction in parameter size compared with Fourier-based activations without loss of expressivity. Embedding DARUAN into KANs yields quantum-inspired KANs (QKANs), which retain the interpretability of KANs while improving their parameter efficiency, expressivity, and generalization. We further introduce two novel techniques to enhance scalability, feasibility and computational efficiency, such as layer extension and hybrid QKANs (HQKANs) as drop-in replacements of multi-layer perceptrons (MLPs) for feed-forward networks in large-scale models. We provide theoretical analysis and extensive experiments on function regression, image classification, and autoregressive generative language modeling, demonstrating the efficiency and scalability of QKANs. DARUANs and QKANs offer a promising direction for advancing quantum machine learning on both noisy intermediate-scale quantum (NISQ) hardware and classical quantum simulators.

Evolvable Graph Diffusion Optimal Transport with Pattern-Specific Alignment for Brain Connectome Modeling

Authors: Xiaoqi Sheng, Jiawen Liu, Jiaming Liang, Yiheng Zhang, Hongmin Cai

Abstract: Network analysis of human brain connectivity indicates that individual differences in cognitive abilities arise from neurobiological mechanisms inherent in structural and functional brain networks. Existing studies routinely treat structural connectivity (SC) as optimal or fixed topological scaffolds for functional connectivity (FC), often overlooking higher-order dependencies between brain regions and limiting the modeling of complex cognitive processes. Besides, the distinct spatial organizations of SC and FC complicate direct integration, as naive alignment may distort intrinsic nonlinear patterns of brain connectivity. In this study, we propose a novel framework called Evolvable Graph Diffusion Optimal Transport with Pattern-Specific Alignment (EDT-PA), designed to identify disease-specific connectome patterns and classify brain disorders. To accurately model high-order structural dependencies, EDT-PA incorporates a spectrum of evolvable modeling blocks to dynamically capture high-order dependencies across brain regions. Additionally, a Pattern-Specific Alignment mechanism employs optimal transport to align structural and functional representations in a geometry-aware manner. By incorporating a Kolmogorov-Arnold network for flexible node aggregation, EDT-PA is capable of modeling complex nonlinear interactions among brain regions for downstream classification. Extensive evaluations on the REST-meta-MDD and ADNI datasets demonstrate that EDT-PA outperforms state-of-the-art methods, offering a more effective framework for revealing structure-function misalignments and disorder-specific subnetworks in brain disorders. The project of this work is released via this link.

Interpretable Clinical Classification with Kolmogorov-Arnold Networks

Authors: Alejandro Almodóvar, Patricia A. Apellániz, Alba Garrido, Fernando Fernández-Salvador, Santiago Zazo, Juan Parras

Abstract: The increasing use of machine learning in clinical decision support has been limited by the lack of transparency of many high-performing models. In clinical settings, predictions must be interpretable, auditable, and actionable. This study investigates Kolmogorov-Arnold Networks (KANs) as intrinsically interpretable alternatives to conventional black-box models for clinical classification of tabular health data, aiming to balance predictive performance with clinically meaningful transparency. We introduce two KAN-based models: the Logistic KAN, a flexible generalization of logistic regression, and the Kolmogorov-Arnold Additive Model (KAAM), an additive variant that yields transparent symbolic representations through feature-wise decomposability. Both models are evaluated on multiple public clinical datasets and compared with standard linear, tree-based, and neural baselines. Across all datasets, the proposed models achieve predictive performance comparable to or exceeding that of commonly used baselines while remaining fully interpretable. Logistic-KAN obtains the highest overall ranking across evaluation metrics, with a mean reciprocal rank of 0.76, indicating consistently strong performance across tasks. KAAM provides competitive accuracy while offering enhanced transparency through feature-wise decomposability, patient-level visualizations, and nearest-patient retrieval, enabling direct inspection of individual predictions. KAN-based models provide a practical and trustworthy alternative to black-box models for clinical classification, offering a strong balance between predictive performance and interpretability for clinical decision support. By enabling transparent, patient-level reasoning and clinically actionable insights, the proposed models represent a promising step toward trustworthy AI in healthcare (code: https://github.com/Patricia-A-Apellaniz/classification_with_kans).

Diffusion Policies with Offline and Inverse Reinforcement Learning for Promoting Physical Activity in Older Adults Using Wearable Sensors

Authors: Chang Liu, Ladda Thiamwong, Yanjie Fu, Rui Xie

Abstract: Utilizing offline reinforcement learning (RL) with real-world clinical data is getting increasing attention in AI for healthcare. However, implementation poses significant challenges. Defining direct rewards is difficult, and inverse RL (IRL) struggles to infer accurate reward functions from expert behavior in complex environments. Offline RL also encounters challenges in aligning learned policies with observed human behavior in healthcare applications. To address challenges in applying offline RL to physical activity promotion for older adults at high risk of falls, based on wearable sensor activity monitoring, we introduce Kolmogorov-Arnold Networks and Diffusion Policies for Offline Inverse Reinforcement Learning (KANDI). By leveraging the flexible function approximation in Kolmogorov-Arnold Networks, we estimate reward functions by learning free-living environment behavior from low-fall-risk older adults (experts), while diffusion-based policies within an Actor-Critic framework provide a generative approach for action refinement and efficiency in offline RL. We evaluate KANDI using wearable activity monitoring data in a two-arm clinical trial from our Physio-feedback Exercise Program (PEER) study, emphasizing its practical application in a fall-risk intervention program to promote physical activity among older adults. Additionally, KANDI outperforms state-of-the-art methods on the D4RL benchmark. These results underscore KANDI’s potential to address key challenges in offline RL for healthcare applications, offering an effective solution for activity promotion intervention strategies in healthcare.

Physics-informed time series analysis with Kolmogorov-Arnold Networks under Ehrenfest constraints

Authors: Abhijit Sen, Illya V. Lukin, Kurt Jacobs, Lev Kaplan, Andrii G. Sotnikov, Denys I. Bondar

Abstract: The prediction of quantum dynamical responses lies at the heart of modern physics. Yet, modeling these time-dependent behaviors remains a formidable challenge because quantum systems evolve in high-dimensional Hilbert spaces, often rendering traditional numerical methods computationally prohibitive. While large language models have achieved remarkable success in sequential prediction, quantum dynamics presents a fundamentally different challenge: forecasting the entire temporal evolution of quantum systems rather than merely the next element in a sequence. Existing neural architectures such as recurrent and convolutional networks often require vast training datasets and suffer from spurious oscillations that compromise physical interpretability. In this work, we introduce a fundamentally new approach: Kolmogorov Arnold Networks (KANs) augmented with physics-informed loss functions that enforce the Ehrenfest theorems. Our method achieves superior accuracy with significantly less training data: it requires only 5.4 percent of the samples (200) compared to Temporal Convolution Networks (3,700). We further introduce the Chain of KANs, a novel architecture that embeds temporal causality directly into the model design, making it particularly well-suited for time series modeling. Our results demonstrate that physics-informed KANs offer a compelling advantage over conventional black-box models, maintaining both mathematical rigor and physical consistency while dramatically reducing data requirements.

On the Rate of Convergence of Kolmogorov-Arnold Network Regression Estimators

Authors: Wei Liu, Eleni Chatzi, Zhilu Lai

Abstract: Kolmogorov-Arnold Networks (KANs) offer a structured and interpretable framework for multivariate function approximation by composing univariate transformations through additive or multiplicative aggregation. This paper establishes theoretical convergence guarantees for KANs when the univariate components are represented by B-splines. We prove that both additive and hybrid additive-multiplicative KANs attain the minimax-optimal convergence rate $O(n^{-2r/(2r+1)})$ for functions in Sobolev spaces of smoothness $r$. We further derive guidelines for selecting the optimal number of knots in the B-splines. The theory is supported by simulation studies that confirm the predicted convergence rates. These results provide a theoretical foundation for using KANs in nonparametric regression and highlight their potential as a structured alternative to existing methods.

Projective Kolmogorov Arnold Neural Networks (P-KANs): Entropy-Driven Functional Space Discovery for Interpretable Machine Learning

Authors: Alastair Poole, Stig McArthur, Saravan Kumar

Abstract: Kolmogorov-Arnold Networks (KANs) relocate learnable nonlinearities from nodes to edges, demonstrating remarkable capabilities in scientific machine learning and interpretable modeling. However, current KAN implementations suffer from fundamental inefficiencies due to redundancy in high-dimensional spline parameter spaces, where numerous distinct parameterisations yield functionally equivalent behaviors. This redundancy manifests as a “nuisance space” in the model’s Jacobian, leading to susceptibility to overfitting and poor generalization. We introduce Projective Kolmogorov-Arnold Networks (P-KANs), a novel training framework that guides edge function discovery towards interpretable functional representations through entropy-minimisation techniques from signal analysis and sparse dictionary learning. Rather than constraining functions to predetermined spaces, our approach maintains spline space flexibility while introducing “gravitational” terms that encourage convergence towards optimal functional representations. Our key insight recognizes that optimal representations can be identified through entropy analysis of projection coefficients, compressing edge functions to lower-parameter projective spaces (Fourier, Chebyshev, Bessel). P-KANs demonstrate superior performance across multiple domains, achieving up to 80% parameter reduction while maintaining representational capacity, significantly improved robustness to noise compared to standard KANs, and successful application to industrial automated fiber placement prediction. Our approach enables automatic discovery of mixed functional representations where different edges converge to different optimal spaces, providing both compression benefits and enhanced interpretability for scientific machine learning applications.

A HyperGraphMamba-Based Multichannel Adaptive Model for ncRNA Classification

Authors: Xin An, Ruijie Li, Qiao Ning, Hui Li, Qian Ma, Shikai Guo

Abstract: Non-coding RNAs (ncRNAs) play pivotal roles in gene expression regulation and the pathogenesis of various diseases. Accurate classification of ncRNAs is essential for functional annotation and disease diagnosis. To address existing limitations in feature extraction depth and multimodal fusion, we propose HGMamba-ncRNA, a HyperGraphMamba-based multichannel adaptive model, which integrates sequence, secondary structure, and optionally available expression features of ncRNAs to enhance classification performance. Specifically, the sequence of ncRNA is modeled using a parallel Multi-scale Convolution and LSTM architecture (MKC-L) to capture both local patterns and long-range dependencies of nucleotides. The structure modality employs a multi-scale graph transformer (MSGraphTransformer) to represent the multi-level topological characteristics of ncRNA secondary structures. The expression modality utilizes a Chebyshev Polynomial-based Kolmogorov-Arnold Network (CPKAN) to effectively model and interpret high-dimensional expression profiles. Finally, by incorporating virtual nodes to facilitate efficient and comprehensive multimodal interaction, HyperGraphMamba is proposed to adaptively align and integrate multichannel heterogeneous modality features. Experiments conducted on three public datasets demonstrate that HGMamba-ncRNA consistently outperforms state-of-the-art methods in terms of accuracy and other metrics. Extensive empirical studies further confirm the model’s robustness, effectiveness, and strong transferability, offering a novel and reliable strategy for complex ncRNA functional classification. Code and datasets are available at https://anonymous.4open.science/r/HGMamba-ncRNA-94D0.

Process-Informed Forecasting of Complex Thermal Dynamics in Pharmaceutical Manufacturing

Authors: Ramona Rubini, Siavash Khodakarami, Aniruddha Bora, George Em Karniadakis, Michele Dassisti

Abstract: Accurate time-series forecasting for complex physical systems is the backbone of modern industrial monitoring and control, yet deep learning models often lack the physical consistency required in regulated environments.To bridge this gap, we introduce Process-Informed Forecasting (PIF) models for temperature in pharmaceutical lyophilization, embedding deterministic production recipes as macro-structural priors. We investigate classical methods (e.g., Autoregressive Integrated Moving Average (ARIMA) model) and modern deep learning architectures, including Kolmogorov-Arnold Networks (KANs). We compare three different loss function formulations that integrate a process-informed trajectory prior: a fixed-weight loss, a dynamic uncertainty-based loss, and a Residual-Based Attention (RBA) mechanism. We evaluate all models not only for accuracy and physical consistency but also for robustness to sensor noise. Furthermore, we test the practical generalizability of the best model in a transfer-learning scenario to a new process. Our results show that PIF models outperform their data-driven counterparts in terms of accuracy, physical plausibility and noise resilience, offering a scalable framework for reliable and generalizable forecasting solutions in critical manufacturing.

TSKAN: Interpretable Machine Learning for QoE modeling over Time Series Data

Authors: Kamal Singh, Priyanka Rawat, Sami Marouani, Baptiste Jeudy

Abstract: Quality of Experience (QoE) modeling is crucial for optimizing video streaming services to capture the complex relationships between different features and user experience. We propose a novel approach to QoE modeling in video streaming applications using interpretable Machine Learning (ML) techniques over raw time series data. Unlike traditional black-box approaches, our method combines Kolmogorov-Arnold Networks (KANs) as an interpretable readout on top of compact frequency-domain features, allowing us to capture temporal information while retaining a transparent and explainable model. We evaluate our method on popular datasets and demonstrate its enhanced accuracy in QoE prediction, while offering transparency and interpretability.

U-MAN: U-Net with Multi-scale Adaptive KAN Network for Medical Image Segmentation

Authors: Bohan Huang, Qianyun Bao, Haoyuan Ma

Abstract: Medical image segmentation faces significant challenges in preserving fine-grained details and precise boundaries due to complex anatomical structures and pathological regions. These challenges primarily stem from two key limitations of conventional U-Net architectures: (1) their simple skip connections ignore the encoder-decoder semantic gap between various features, and (2) they lack the capability for multi-scale feature extraction in deep layers. To address these challenges, we propose the U-Net with Multi-scale Adaptive KAN (U-MAN), a novel architecture that enhances the emerging Kolmogorov-Arnold Network (KAN) with two specialized modules: Progressive Attention-Guided Feature Fusion (PAGF) and the Multi-scale Adaptive KAN (MAN). Our PAGF module replaces the simple skip connection, using attention to fuse features from the encoder and decoder. The MAN module enables the network to adaptively process features at multiple scales, improving its ability to segment objects of various sizes. Experiments on three public datasets (BUSI, GLAS, and CVC) show that U-MAN outperforms state-of-the-art methods, particularly in defining accurate boundaries and preserving fine details.

CausalKANs: interpretable treatment effect estimation with Kolmogorov-Arnold networks

Authors: Alejandro Almodóvar, Patricia A. Apellániz, Santiago Zazo, Juan Parras

Abstract: Deep neural networks achieve state-of-the-art performance in estimating heterogeneous treatment effects, but their opacity limits trust and adoption in sensitive domains such as medicine, economics, and public policy. Building on well-established and high-performing causal neural architectures, we propose causalKANs, a framework that transforms neural estimators of conditional average treatment effects (CATEs) into Kolmogorov–Arnold Networks (KANs). By incorporating pruning and symbolic simplification, causalKANs yields interpretable closed-form formulas while preserving predictive accuracy. Experiments on benchmark datasets demonstrate that causalKANs perform on par with neural baselines in CATE error metrics, and that even simple KAN variants achieve competitive performance, offering a favorable accuracy–interpretability trade-off. By combining reliability with analytic accessibility, causalKANs provide auditable estimators supported by closed-form expressions and interpretable plots, enabling trustworthy individualized decision-making in high-stakes settings. We release the code for reproducibility at https://github.com/aalmodovares/causalkans .

Proposal of method to solve a Traveling Salesman Problem using Variational Quantum Kolmogorov-Arnold Network

Author: Hikaru Wakaura

Abstract: Traveling salesman problems (TSP) are one of the well-known combinatorial optimization problems that many groups tackle to solve. This problem appears in many types of combinational optimization, such as scheduling, route optimization, and circuit optimization. However, this problem is NP-hard, as the number of combinations increases exponentially as the number of sites increases. Quantum Annealers and Adiabatic Quantum Computers are good at solving it, and universal quantum computers are limited by the number of qubits they have. Therefore, we propose a novel approach that solves it using a Variational Quantum Kolmogorov-Arnold network (VQKAN). Our approach requires a smaller number of qubits than the former approaches on quantum computers. We confirmed that our approach can optimize the paths on the graphs whose length of each path is time-dependent, partial.

Learning KAN-based Implicit Neural Representations for Deformable Image Registration

Authors: Nikita Drozdov, Marat Zinovev, Dmitry Sorokin

Abstract: Deformable image registration (DIR) is a cornerstone of medical image analysis, enabling spatial alignment for tasks like comparative studies and multi-modal fusion. While learning-based methods (e.g., CNNs, transformers) offer fast inference, they often require large training datasets and struggle to match the precision of classical iterative approaches on some organ types and imaging modalities. Implicit neural representations (INRs) have emerged as a promising alternative, parameterizing deformations as continuous mappings from coordinates to displacement vectors. However, this comes at the cost of requiring instance-specific optimization, making computational efficiency and seed-dependent learning stability critical factors for these methods. In this work, we propose KAN-IDIR and RandKAN-IDIR, the first integration of Kolmogorov-Arnold Networks (KANs) into deformable image registration with implicit neural representations (INRs). Our proposed randomized basis sampling strategy reduces the required number of basis functions in KAN while maintaining registration quality, thereby significantly lowering computational costs. We evaluated our approach on three diverse datasets (lung CT, brain MRI, cardiac MRI) and compared it with competing instance-specific learning-based approaches, dataset-trained deep learning models, and classical registration approaches. KAN-IDIR and RandKAN-IDIR achieved the highest accuracy among INR-based methods across all evaluated modalities and anatomies, with minimal computational overhead and superior learning stability across multiple random seeds. Additionally, we discovered that our RandKAN-IDIR model with randomized basis sampling slightly outperforms the model with learnable basis function indices, while eliminating its additional training-time complexity.

FMC-DETR: Frequency-Decoupled Multi-Domain Coordination for Aerial-View Object Detection

Authors: Ben Liang, Hongguang Wei, Yuan Liu, Bingwen Qiu, Yihong Wang, Xiubao Sui, Qian Chen

Abstract: Remote sensing object detection is a critical technology for real-world applications such as natural resource monitoring, traffic management, and UAV-based rescue. Detecting tiny objects in high-resolution aerial imagery remains challenging due to weak visual cues and insufficient global context modeling in complex scenes. Existing methods often suffer from delayed contextual interaction and limited nonlinear reasoning, which restrict their ability to effectively refine shallow representations and ultimately lead to suboptimal performance. To address these challenges, we propose FMC-DETR, a frequency-decoupled fusion framework for aerial-view object detection. First, we propose the Wavelet Kolmogorov-Arnold Transformer (WeKat) backbone, which employs cascaded wavelet transforms to enhance global low-frequency structure perception in shallow features while preserving fine-grained details, and further leverages Kolmogorov-Arnold networks for adaptive nonlinear modeling of multi-scale dependencies. Second, we introduce the Multi-Domain Feature Coordination (MDFC) module, which refines cross-scale fused representations through partial-channel spatial, spectral, and structural coordination, thereby strengthening small-object-related feature responses in cluttered scenes. Finally, we design the Compact Partial Fusion (CPF) module, which performs compact multi-branch aggregation with progressive partial refinement to improve feature diversity and multi-scale interaction while preserving stable information flow and reducing redundant perturbation. Extensive experiments across multiple remote sensing benchmarks demonstrate that FMC-DETR achieves state-of-the-art performance and significantly outperforming the baseline detector. Code is available at https://github.com/bloomingvision/FMC-DETR.

Splines-Based Feature Importance in Kolmogorov-Arnold Networks: A Framework for Supervised Tabular Data Dimensionality Reduction

Authors: Ange-Clément Akazan, Verlon Roel Mbingui

Abstract: Feature selection is a key step in many tabular prediction problems, where multiple candidate variables may be redundant, noisy, or weakly informative. We investigate feature selection based on Kolmogorov-Arnold Networks (KANs), which parameterize feature transformations with splines and expose per-feature importance scores in a natural way. From this idea we derive four KAN-based selection criteria (coefficient norms, gradient-based saliency, and knockout scores) and compare them with standard methods such as LASSO, Random Forest feature importance, Mutual Information, and SVM-RFE on a suite of real and synthetic classification and regression datasets. Using average F1 and $R^2$ scores across three feature-retention levels (20%, 40%, 60%), we find that KAN-based selectors are generally competitive with, and sometimes superior to, classical baselines. In classification, KAN criteria often match or exceed existing methods on multi-class tasks by removing redundant features and capturing nonlinear interactions. In regression, KAN-based scores provide robust performance on noisy and heterogeneous datasets, closely tracking strong ensemble predictors; we also observe characteristic failure modes, such as overly aggressive pruning with an $\ell_1$ criterion. Stability and redundancy analyses further show that KAN-based selectors yield reproducible feature subsets across folds while avoiding unnecessary correlation inflation, ensuring reliable and non-redundant variable selection. Overall, our findings demonstrate that KAN-based feature selection provides a powerful and interpretable alternative to traditional methods, capable of uncovering nonlinear and multivariate feature relevance beyond sparsity or impurity-based measures.

FS-KAN: Permutation Equivariant Kolmogorov-Arnold Networks via Function Sharing

Authors: Ran Elbaz, Guy Bar-Shalom, Yam Eitan, Fabrizio Frasca, Haggai Maron

Abstract: Permutation equivariant neural networks employing parameter-sharing schemes have emerged as powerful models for leveraging a wide range of data symmetries, significantly enhancing the generalization and computational efficiency of the resulting models. Recently, Kolmogorov-Arnold Networks (KANs) have demonstrated promise through their improved interpretability and expressivity compared to traditional architectures based on MLPs. While equivariant KANs have been explored in recent literature for a few specific data types, a principled framework for applying them to data with permutation symmetries in a general context remains absent. This paper introduces Function Sharing KAN (FS-KAN), a principled approach to constructing equivariant and invariant KA layers for arbitrary permutation symmetry groups, unifying and significantly extending previous work in this domain. We derive the basic construction of these FS-KAN layers by generalizing parameter-sharing schemes to the Kolmogorov-Arnold setup and provide a theoretical analysis demonstrating that FS-KANs have the same expressive power as networks that use standard parameter-sharing layers, allowing us to transfer well-known and important expressivity results from parameter-sharing networks to FS-KANs. Empirical evaluations on multiple data types and symmetry groups show that FS-KANs exhibit superior data efficiency compared to standard parameter-sharing layers, by a wide margin in certain cases, while preserving the interpretability and adaptability of KANs, making them an excellent architecture choice in low-data regimes.

LEMs: A Primer On Large Execution Models

Authors: Remi Genet, Hugo Inzirillo

Abstract: This paper introduces Large Execution Models (LEMs), a novel deep learning framework that extends transformer-based architectures to address complex execution problems with flexible time boundaries and multiple execution constraints. Building upon recent advances in neural VWAP execution strategies, LEMs generalize the approach from fixed-duration orders to scenarios where execution duration is bounded between minimum and maximum time horizons, similar to share buyback contract structures. The proposed architecture decouples market information processing from execution allocation decisions: a common feature extraction pipeline using Temporal Kolmogorov-Arnold Networks (TKANs), Variable Selection Networks (VSNs), and multi-head attention mechanisms processes market data to create informational context, while independent allocation networks handle the specific execution logic for different scenarios (fixed quantity vs. fixed notional, buy vs. sell orders). This architectural separation enables a unified model to handle diverse execution objectives while leveraging shared market understanding across scenarios. Through comprehensive empirical evaluation on intraday cryptocurrency markets and multi-day equity trading using DOW Jones constituents, we demonstrate that LEMs achieve superior execution performance compared to traditional benchmarks by dynamically optimizing execution paths within flexible time constraints. The unified model architecture enables deployment across different execution scenarios (buy/sell orders, varying duration boundaries, volume/notional targets) through a single framework, providing significant operational advantages over asset-specific approaches.

Heterogeneous Multi-agent Collaboration in UAV-assisted Mobile Crowdsensing Networks

Authors: Xianyang Deng, Wenshuai Liu, Yaru FuB, Qi Zhu

Abstract: Unmanned aerial vehicles (UAVs)-assisted mobile crowdsensing (MCS) has emerged as a promising paradigm for data collection. However, challenges such as spectrum scarcity, device heterogeneity, and user mobility hinder efficient coordination of sensing, communication, and computation. To tackle these issues, we propose a joint optimization framework that integrates time slot partition for sensing, communication, and computation phases, resource allocation, and UAV 3D trajectory planning, aiming to maximize the amount of processed sensing data. The problem is formulated as a non-convex stochastic optimization and further modeled as a partially observable Markov decision process (POMDP) that can be solved by multi-agent deep reinforcement learning (MADRL) algorithm. To overcome the limitations of conventional multi-layer perceptron (MLP) networks, we design a novel MADRL algorithm with hybrid actor network. The newly developed method is based on heterogeneous agent proximal policy optimization (HAPPO), empowered by convolutional neural networks (CNN) for feature extraction and Kolmogorov-Arnold networks (KAN) to capture structured state-action dependencies. Extensive numerical results demonstrate that our proposed method achieves significant improvements in the amount of processed sensing data when compared with other benchmarks.

Effective Model Pruning: Measure The Redundancy of Model Components

Authors: Yixuan Wang, Dan Guralnik, Saiedeh Akbari, Warren Dixon

Abstract: This article initiates the study of a basic question about model pruning. Given a vector $s$ of importance scores assigned to model components, how many of the scored components could be discarded without sacrificing performance? We propose Effective Model Pruning (EMP), which derives the desired sparsity directly from the score distribution using the notion of effective sample size from particle filtering, also known as the inverse Simpson index. Rather than prescribe a pruning criterion, EMP supplies a universal adaptive threshold derived from the distribution of the score $s$ over the model components: EMP maps $s$ to a number $N_{eff}=N_{eff}(s)$, called the effective sample size. The $N-N_{eff}$ lowest scoring components are discarded. A tight lower bound on the preserved mass fraction $s_{eff}$ (the sum of retained normalized scores) in terms of $N_{eff}$ is derived. This process yields models with a provable upper bound on the loss change relative to the original dense model. Numerical experiments are performed demonstrating this phenomenon across a variety of network architectures including MLPs, CNNs, Transformers, LLMs, and KAN. It is also shown that EMP addresses a rich set of pruning criteria such as weight magnitude, attention score, KAN importance score, and even feature-level signals such as image pixels.

October

LAKAN: Landmark-assisted Adaptive Kolmogorov-Arnold Network for Face Forgery Detection

Authors: Jiayao Jiang, Bin Liu, Qi Chu, Nenghai Yu

Abstract: The rapid development of deepfake generation techniques necessitates robust face forgery detection algorithms. While methods based on Convolutional Neural Networks (CNNs) and Transformers are effective, there is still room for improvement in modeling the highly complex and non-linear nature of forgery artifacts. To address this issue, we propose a novel detection method based on the Kolmogorov-Arnold Network (KAN). By replacing fixed activation functions with learnable splines, our KAN-based approach is better suited to this challenge. Furthermore, to guide the network’s focus towards critical facial areas, we introduce a Landmark-assisted Adaptive Kolmogorov-Arnold Network (LAKAN) module. This module uses facial landmarks as a structural prior to dynamically generate the internal parameters of the KAN, creating an instance-specific signal that steers a general-purpose image encoder towards the most informative facial regions with artifacts. This core innovation creates a powerful combination between geometric priors and the network’s learning process. Extensive experiments on multiple public datasets show that our proposed method achieves superior performance.

Shift-Invariant Attribute Scoring for Kolmogorov-Arnold Networks via Shapley Value

Authors: Wangxuan Fan, Ching Wang, Siqi Li, Nan Liu

Abstract: For many real-world applications, understanding feature-outcome relationships is as crucial as achieving high predictive accuracy. While traditional neural networks excel at prediction, their black-box nature obscures underlying functional relationships. Kolmogorov–Arnold Networks (KANs) address this by employing learnable spline-based activation functions on edges, enabling recovery of symbolic representations while maintaining competitive performance. However, KAN’s architecture presents unique challenges for network pruning. Conventional magnitude-based methods become unreliable due to sensitivity to input coordinate shifts. We propose \textbf{ShapKAN}, a pruning framework using Shapley value attribution to assess node importance in a shift-invariant manner. Unlike magnitude-based approaches, ShapKAN quantifies each node’s actual contribution, ensuring consistent importance rankings regardless of input parameterization. Extensive experiments on synthetic and real-world datasets demonstrate that ShapKAN preserves true node importance while enabling effective network compression. Our approach improves KAN’s interpretability advantages, facilitating deployment in resource-constrained environments.

Kolmogorov-Arnold Networks in Thermoelectric Materials Design

Authors: Marco Fronzi, Michael J. Ford, Kamal Singh Nayal, Olexandr Isayev, Catherine Stampfl

Abstract: The discovery of high-performance thermoelectric materials requires models that are both accurate and interpretable. Traditional machine learning approaches, while effective at property prediction, often act as black boxes and provide limited physical insight. In this work, we introduce Kolmogorov–Arnold Networks (KANs) for the prediction of thermoelectric properties, focusing on the Seebeck coefficient and band gap. Compared to multilayer perceptrons (MLPs), KANs achieve comparable predictive accuracy while offering explicit symbolic representations of structure–property relationships. This dual capability enables both reliable predictions and the extraction of physically meaningful functional forms. Benchmarking against literature models further highlights the robustness and generalisability of the approach. Our findings demonstrate that KANs provide a powerful framework for reverse engineering materials with targeted thermoelectric properties, bridging the gap between predictive performance and scientific interpretability.

BEKAN: Boundary condition-guaranteed evolutionary Kolmogorov-Arnold networks with radial basis functions for solving PDE problems

Authors: Bongseok Kim, Jiahao Zhang, Guang Lin

Abstract: Deep learning has gained attention for solving PDEs, but the black-box nature of neural networks hinders precise enforcement of boundary conditions. To address this, we propose a boundary condition-guaranteed evolutionary Kolmogorov-Arnold Network (KAN) with radial basis functions (BEKAN). In BEKAN, we propose three distinct and combinable approaches for incorporating Dirichlet, periodic, and Neumann boundary conditions into the network. For Dirichlet problem, we use smooth and global Gaussian RBFs to construct univariate basis functions for approximating the solution and to encode boundary information at the activation level of the network. To handle periodic problems, we employ a periodic layer constructed from a set of sinusoidal functions to enforce the boundary conditions exactly. For a Neumann problem, we devise a least-squares formulation to guide the parameter evolution toward satisfying the Neumann condition. By virtue of the boundary-embedded RBFs, the periodic layer, and the evolutionary framework, we can perform accurate PDE simulations while rigorously enforcing boundary conditions. For demonstration, we conducted extensive numerical experiments on Dirichlet, Neumann, periodic, and mixed boundary value problems. The results indicate that BEKAN outperforms both multilayer perceptron (MLP) and B-splines KAN in terms of accuracy. In conclusion, the proposed approach enhances the capability of KANs in solving PDE problems while satisfying boundary conditions, thereby facilitating advancements in scientific computing and engineering applications.

PolyKAN: A Polyhedral Analysis Framework for Provable and Approximately Optimal KAN Compression

Author: Di Zhang

Abstract: Kolmogorov-Arnold Networks (KANs) have emerged as a promising alternative to traditional Multi-Layer Perceptrons (MLPs), offering enhanced interpretability and a solid mathematical foundation. However, their parameter efficiency remains a significant challenge for practical deployment. This paper introduces PolyKAN, a novel theoretical framework for KAN compression that provides formal guarantees on both model size reduction and approximation error. By leveraging the inherent piecewise polynomial structure of KANs, we formulate the compression problem as a polyhedral region merging task. We establish a rigorous polyhedral characterization of KANs, develop a complete theory of $ε$-equivalent compression, and design a dynamic programming algorithm that achieves approximately optimal compression under specified error bounds. Our theoretical analysis demonstrates that PolyKAN achieves provably near-optimal compression while maintaining strict error control, with guaranteed global optimality for univariate spline functions. This framework provides the first formal foundation for KAN compression with mathematical guarantees, opening new directions for the efficient deployment of interpretable neural architectures.

PIKAN: Physics-Inspired Kolmogorov-Arnold Networks for Explainable UAV Channel Modelling

Authors: Kürşat Tekbıyık, Güneş Karabulut Kurt, Antoine Lesage-Landry

Abstract: Unmanned aerial vehicle (UAV) communications demand accurate yet interpretable air-to-ground (A2G) channel models that can adapt to nonstationary propagation environments. While deterministic models offer interpretability and deep learning (DL) models provide accuracy, both approaches suffer from either rigidity or a lack of explainability. To bridge this gap, we propose the Physics-Inspired Kolmogorov-Arnold Network (PIKAN) that embeds physical principles (e.g., free-space path loss, two-ray reflections) into the learning process. Unlike physics-informed neural networks (PINNs), PIKAN is more flexible for applying physical information because it introduces them as flexible inductive biases. Thus, it enables a more flexible training process. Experiments on UAV A2G measurement data show that PIKAN achieves comparable accuracy to DL models while providing symbolic and explainable expressions aligned with propagation laws. Remarkably, PIKAN achieves this performance with only 232 parameters, making it up to 37 times lighter than multilayer perceptron (MLP) baselines with thousands of parameters, without sacrificing correlation with measurements and also providing symbolic expressions. These results highlight PIKAN as an efficient, interpretable, and scalable solution for UAV channel modelling in beyond-5G and 6G networks.

XLSR-Kanformer: A KAN-Intergrated model for Synthetic Speech Detection

Authors: Phuong Tuan Dat, Tran Huy Dat

Abstract: Recent advancements in speech synthesis technologies have led to increasingly sophisticated spoofing attacks, posing significant challenges for automatic speaker verification systems. While systems based on self-supervised learning (SSL) models, particularly the XLSR-Conformer architecture, have demonstrated remarkable performance in synthetic speech detection, there remains room for architectural improvements. In this paper, we propose a novel approach that replaces the traditional Multi-Layer Perceptron (MLP) in the XLSR-Conformer model with a Kolmogorov-Arnold Network (KAN), a powerful universal approximator based on the Kolmogorov-Arnold representation theorem. Our experimental results on ASVspoof2021 demonstrate that the integration of KAN to XLSR-Conformer model can improve the performance by 60.55% relatively in Equal Error Rate (EER) LA and DF sets, further achieving 0.70% EER on the 21LA set. Besides, the proposed replacement is also robust to various SSL architectures. These findings suggest that incorporating KAN into SSL-based models is a promising direction for advances in synthetic speech detection.

Function regression using the forward forward training and inferring paradigm

Authors: Shivam Padmani, Akshay Joshi

Abstract: Function regression/approximation is a fundamental application of machine learning. Neural networks (NNs) can be easily trained for function regression using a sufficient number of neurons and epochs. The forward-forward learning algorithm is a novel approach for training neural networks without backpropagation, and is well suited for implementation in neuromorphic computing and physical analogs for neural networks. To the best of the authors’ knowledge, the Forward Forward paradigm of training and inferencing NNs is currently only restricted to classification tasks. This paper introduces a new methodology for approximating functions (function regression) using the Forward-Forward algorithm. Furthermore, the paper evaluates the developed methodology on univariate and multivariate functions, and provides preliminary studies of extending the proposed Forward-Forward regression to Kolmogorov Arnold Networks, and Deep Physical Neural Networks.

DGTEN: A Robust Deep Gaussian based Graph Neural Network for Dynamic Trust Evaluation with Uncertainty-Quantification Support

Authors: Muhammad Usman, Yugyung Lee

Abstract: Dynamic trust evaluation in large, rapidly evolving graphs demands models that capture changing relationships, express calibrated confidence, and resist adversarial manipulation. DGTEN (Deep Gaussian-Based Trust Evaluation Network) introduces a unified graph-based framework that does all three by combining uncertainty-aware message passing, expressive temporal modeling, and built-in defenses against trust-targeted attacks. It represents nodes and edges as Gaussian distributions so that both semantic signals and epistemic uncertainty propagate through the graph neural network, enabling risk-aware trust decisions rather than overconfident guesses. To track how trust evolves, it layers hybrid absolute-Gaussian-hourglass positional encoding with Kolmogorov-Arnold network-based unbiased multi-head attention, then applies an ordinary differential equation-based residual learning module to jointly model abrupt shifts and smooth trends. Robust adaptive ensemble coefficient analysis prunes or down-weights suspicious interactions using complementary cosine and Jaccard similarity, curbing reputation laundering, sabotage, and on-off attacks. On two signed Bitcoin trust networks, DGTEN delivers standout gains where it matters most: in single-timeslot prediction on Bitcoin-OTC, it improves MCC by +12.34% over the best dynamic baseline; in the cold-start scenario on Bitcoin-Alpha, it achieves a +25.00% MCC improvement, the largest across all tasks and datasets; while under adversarial on-off attacks, it surpasses the baseline by up to +10.23% MCC. These results endorse the unified DGTEN framework.

EGSTalker: Real-Time Audio-Driven Talking Head Generation with Efficient Gaussian Deformation

Authors: Tianheng Zhu, Yinfeng Yu, Liejun Wang, Fuchun Sun, Wendong Zheng

Abstract: This paper presents EGSTalker, a real-time audio-driven talking head generation framework based on 3D Gaussian Splatting (3DGS). Designed to enhance both speed and visual fidelity, EGSTalker requires only 3-5 minutes of training video to synthesize high-quality facial animations. The framework comprises two key stages: static Gaussian initialization and audio-driven deformation. In the first stage, a multi-resolution hash triplane and a Kolmogorov-Arnold Network (KAN) are used to extract spatial features and construct a compact 3D Gaussian representation. In the second stage, we propose an Efficient Spatial-Audio Attention (ESAA) module to fuse audio and spatial cues, while KAN predicts the corresponding Gaussian deformations. Extensive experiments demonstrate that EGSTalker achieves rendering quality and lip-sync accuracy comparable to state-of-the-art methods, while significantly outperforming them in inference speed. These results highlight EGSTalker’s potential for real-time multimedia applications.

QuIRK: Quantum-Inspired Re-uploading KAN

Authors: Vinayak Sharma, Ashish Padhy, Lord Sen, Vijay Jagdish Karanjkar, Sourav Behera, Shyamapada Mukherjee, Aviral Shrivastava

Abstract: Kolmogorov-Arnold Networks or KANs have shown the ability to outperform classical Deep Neural Networks, while using far fewer trainable parameters for regression problems on scientific domains. Even more powerful has been their interpretability due to their structure being composed of univariate B-Spline functions. This enables us to derive closed-form equations from trained KANs for a wide range of problems. This paper introduces a quantum-inspired variant of the KAN based on Quantum Data Re-uploading (DR) models. The Quantum-Inspired Re-uploading KAN or QuIRK model replaces B-Splines with single-qubit DR models as the univariate function approximator, allowing them to match or outperform traditional KANs while using even fewer parameters. This is especially apparent in the case of periodic functions. Additionally, since the model utilizes only single-qubit circuits, it remains classically tractable to simulate with straightforward GPU acceleration. Finally, we also demonstrate that QuIRK retains the interpretability advantages and the ability to produce closed-form solutions.

PO-CKAN:Physics Informed Deep Operator Kolmogorov Arnold Networks with Chunk Rational Structure

Authors: Junyi Wu, Guang Lin

Abstract: We propose PO-CKAN, a physics-informed deep operator framework based on Chunkwise Rational Kolmogorov–Arnold Networks (KANs), for approximating the solution operators of partial differential equations. This framework leverages a Deep Operator Network (DeepONet) architecture that incorporates Chunkwise Rational Kolmogorov-Arnold Network (CKAN) sub-networks for enhanced function approximation. The principles of Physics-Informed Neural Networks (PINNs) are integrated into the operator learning framework to enforce physical consistency. This design enables the efficient learning of physically consistent spatio-temporal solution operators and allows for rapid prediction for parametric time-dependent PDEs with varying inputs (e.g., parameters, initial/boundary conditions) after training. Validated on challenging benchmark problems, PO-CKAN demonstrates accurate operator learning with results closely matching high-fidelity solutions. PO-CKAN adopts a DeepONet-style branch–trunk architecture with its sub-networks instantiated as rational KAN modules, and enforces physical consistency via a PDE residual (PINN-style) loss. On Burgers’ equation with $ν=0.01$, PO-CKAN reduces the mean relative $L^2$ error by approximately 48\% compared to PI-DeepONet, and achieves competitive accuracy on the Eikonal and diffusion–reaction benchmarks.

INR-Bench: A Unified Benchmark for Implicit Neural Representations in Multi-Domain Regression and Reconstruction

Authors: Linfei Li, Fengyi Zhang, Zhong Wang, Lin Zhang, Ying Shen

Abstract: Implicit Neural Representations (INRs) have gained success in various signal processing tasks due to their advantages of continuity and infinite resolution. However, the factors influencing their effectiveness and limitations remain underexplored. To better understand these factors, we leverage insights from Neural Tangent Kernel (NTK) theory to analyze how model architectures (classic MLP and emerging KAN), positional encoding, and nonlinear primitives affect the response to signals of varying frequencies. Building on this analysis, we introduce INR-Bench, the first comprehensive benchmark specifically designed for multimodal INR tasks. It includes 56 variants of Coordinate-MLP models (featuring 4 types of positional encoding and 14 activation functions) and 22 Coordinate-KAN models with distinct basis functions, evaluated across 9 implicit multimodal tasks. These tasks cover both forward and inverse problems, offering a robust platform to highlight the strengths and limitations of different neural models, thereby establishing a solid foundation for future research. The code and dataset are available at https://github.com/lif314/INR-Bench.

UKANFormer: Noise-Robust Semantic Segmentation for Coral Reef Mapping via a Kolmogorov-Arnold Network-Transformer Hybrid

Authors: Tianyang Dou, Ming Li, Jiangying Qin, Xuan Liao, Jiageng Zhong, Armin Gruen, Mengyi Deng

Abstract: Coral reefs are vital yet fragile ecosystems that require accurate large-scale mapping for effective conservation. Although global products such as the Allen Coral Atlas provide unprecedented coverage of global coral reef distri-bution, their predictions are frequently limited in spatial precision and semantic consistency, especially in regions requiring fine-grained boundary delineation. To address these challenges, we propose UKANFormer, a novel se-mantic segmentation model designed to achieve high-precision mapping under noisy supervision derived from Allen Coral Atlas. Building upon the UKAN architecture, UKANFormer incorporates a Global-Local Transformer (GL-Trans) block in the decoder, enabling the extraction of both global semantic structures and local boundary details. In experiments, UKANFormer achieved a coral-class IoU of 67.00% and pixel accuracy of 83.98%, outperforming conventional baselines under the same noisy labels setting. Remarkably, the model produces predictions that are visually and structurally more accurate than the noisy labels used for training. These results challenge the notion that data quality directly limits model performance, showing that architectural design can mitigate label noise and sup-port scalable mapping under imperfect supervision. UKANFormer provides a foundation for ecological monitoring where reliable labels are scarce.

A Primer on Kolmogorov-Arnold Networks (KANs) for Probabilistic Time Series Forecasting

Authors: Cristian J. Vaca-Rubio, Roberto Pereira, Luis Blanco, Engin Zeydan, Màrius Caus

Abstract: This work introduces Probabilistic Kolmogorov-Arnold Network (P-KAN), a novel probabilistic extension of Kolmogorov-Arnold Networks (KANs) for time series forecasting. By replacing scalar weights with spline-based functional connections and directly parameterizing predictive distributions, P-KANs offer expressive yet parameter-efficient models capable of capturing nonlinear and heavy-tailed dynamics. We evaluate P-KANs on satellite traffic forecasting, where uncertainty-aware predictions enable dynamic thresholding for resource allocation. Results show that P-KANs consistently outperform Multi Layer Perceptron (MLP) baselines in both accuracy and calibration, achieving superior efficiency-risk trade-offs while using significantly fewer parameters. We build up P-KANs on two distributions, namely Gaussian and Student-t distributions. The Gaussian variant provides robust, conservative forecasts suitable for safety-critical scenarios, whereas the Student-t variant yields sharper distributions that improve efficiency under stable demand. These findings establish P-KANs as a powerful framework for probabilistic forecasting with direct applicability to satellite communications and other resource-constrained domains.

MetaCluster: Enabling Deep Compression of Kolmogorov-Arnold Network

Authors: Matthew Raffel, Adwaith Renjith, Lizhong Chen

Abstract: Kolmogorov-Arnold Networks (KANs) replace scalar weights with per-edge vectors of basis coefficients, thereby increasing expressivity and accuracy while also resulting in a multiplicative increase in parameters and memory. We propose MetaCluster, a framework that makes KANs highly compressible without sacrificing accuracy. Specifically, a lightweight meta-learner, trained jointly with the KAN, maps low-dimensional embeddings to coefficient vectors, thereby shaping them to lie on a low-dimensional manifold that is amenable to clustering. We then run K-means in coefficient space and replace per-edge vectors with shared centroids. Afterwards, the meta-learner can be discarded, and a brief fine-tuning of the centroid codebook recovers any residual accuracy loss. The resulting model stores only a small codebook and per-edge indices, exploiting the vector nature of KAN parameters to amortize storage across multiple coefficients. On MNIST, CIFAR-10, and CIFAR-100, across standard KANs and ConvKANs using multiple basis functions, MetaCluster achieves a reduction of up to $80\times$ in parameter storage, with no loss in accuracy. Similarly, on high-dimensional equation modeling tasks, MetaCluster achieves a parameter reduction of $124.1\times$, without impacting performance. Code will be released upon publication.

KCM: KAN-Based Collaboration Models Enhance Pretrained Large Models

Authors: Guangyu Dai, Siliang Tang, Yueting Zhuang

Abstract: In recent years, Pretrained Large Models(PLMs) researchers proposed large-small model collaboration frameworks, leveraged easily trainable small models to assist large models, aim to(1) significantly reduce computational resource consumption while maintaining comparable accuracy, and (2) enhance large model performance in specialized domain tasks. However, this collaborative paradigm suffers from issues such as significant accuracy degradation, exacerbated catastrophic forgetting, and amplified hallucination problems induced by small model knowledge. To address these challenges, we propose a KAN-based Collaborative Model (KCM) as an improved approach to large-small model collaboration. The KAN utilized in KCM represents an alternative neural network architecture distinct from conventional MLPs. Compared to MLPs, KAN offers superior visualizability and interpretability while mitigating catastrophic forgetting. We deployed KCM in large-small model collaborative systems across three scenarios: language, vision, and vision-language cross-modal tasks. The experimental results demonstrate that, compared with pure large model approaches, the large-small model collaboration framework utilizing KCM as the collaborative model significantly reduces the number of large model inference calls while maintaining near-identical task accuracy, thereby substantially lowering computational resource consumption. Concurrently, the KAN-based small collaborative model markedly mitigates catastrophic forgetting, leading to significant accuracy improvements for long-tail data. The results reveal that KCM demonstrates superior performance across all metrics compared to MLP-based small collaborative models (MCM).

K-DAREK: Distance Aware Error for Kurkova Kolmogorov Networks

Authors: Masoud Ataei, Vikas Dhiman, Mohammad Javad Khojasteh

Abstract: Neural networks are powerful parametric function approximators, while Gaussian processes (GPs) are nonparametric probabilistic models that place distributions over functions via kernel-defined correlations but become computationally expensive for large-scale problems. Kolmogorov-Arnold networks (KANs), semi-parametric neural architectures, model complex functions efficiently using spline layers. Kurkova Kolmogorov-Arnold networks (KKANs) extend KANs by replacing the early spline layers with multi-layer perceptrons that map inputs into higher-dimensional spaces before applying spline-based transformations, which yield more stable training and provide robust architectures for system modeling. By enhancing the KKAN architecture, we develop a novel learning algorithm, distance-aware error for Kurkova-Kolmogorov networks (K-DAREK), for efficient and interpretable function approximation with uncertainty quantification. Our approach establishes robust error bounds that are distance-aware; this means they reflect the proximity of a test point to its nearest training points. In safe control case studies, we demonstrate that K-DAREK is about four times faster and ten times more computationally efficient than Ensemble of KANs, 8.6 times more scalable than GP as data size increases, and 7.2% safer than our previous work distance-aware error for Kolmogorov networks (DAREK). Moreover, on real data (e.g., Real Estate Valuation), K-DAREK’s error bound achieves zero coverage violations.

Awakening Facial Emotional Expressions in Human-Robot

Authors: Yongtong Zhu, Lei Li, Iggy Qian, WenBin Zhou, Ye Yuan, Qingdu Li, Na Liu, Jianwei Zhang

Abstract: The facial expression generation capability of humanoid social robots is critical for achieving natural and human-like interactions, playing a vital role in enhancing the fluidity of human-robot interactions and the accuracy of emotional expression. Currently, facial expression generation in humanoid social robots still relies on pre-programmed behavioral patterns, which are manually coded at high human and time costs. To enable humanoid robots to autonomously acquire generalized expressive capabilities, they need to develop the ability to learn human-like expressions through self-training. To address this challenge, we have designed a highly biomimetic robotic face with physical-electronic animated facial units and developed an end-to-end learning framework based on KAN (Kolmogorov-Arnold Network) and attention mechanisms. Unlike previous humanoid social robots, we have also meticulously designed an automated data collection system based on expert strategies of facial motion primitives to construct the dataset. Notably, to the best of our knowledge, this is the first open-source facial dataset for humanoid social robots. Comprehensive evaluations indicate that our approach achieves accurate and diverse facial mimicry across different test subjects.

Seeing Structural Failure Before it Happens: An Image-Based Physics-Informed Neural Network (PINN) for Spaghetti Bridge Load Prediction

Authors: Omer Jauhar Khan, Sudais Khan, Hafeez Anwar, Shahzeb Khan, Shams Ul Arifeen, Farman Ullah

Abstract: Physics Informed Neural Networks (PINNs) are gaining attention for their ability to embed physical laws into deep learning models, which is particularly useful in structural engineering tasks with limited data. This paper aims to explore the use of PINNs to predict the weight of small scale spaghetti bridges, a task relevant to understanding load limits and potential failure modes in simplified structural models. Our proposed framework incorporates physics-based constraints to the prediction model for improved performance. In addition to standard PINNs, we introduce a novel architecture named Physics Informed Kolmogorov Arnold Network (PIKAN), which blends universal function approximation theory with physical insights. The structural parameters provided as input to the model are collected either manually or through computer vision methods. Our dataset includes 15 real bridges, augmented to 100 samples, and our best model achieves an $R^2$ score of 0.9603 and a mean absolute error (MAE) of 10.50 units. From applied perspective, we also provide a web based interface for parameter entry and prediction. These results show that PINNs can offer reliable estimates of structural weight, even with limited data, and may help inform early stage failure analysis in lightweight bridge designs. The complete data and code are available at https://github.com/OmerJauhar/PINNS-For-Spaghetti-Bridges.

Training Deep Physics-Informed Kolmogorov-Arnold Networks

Authors: Spyros Rigas, Fotios Anagnostopoulos, Michalis Papachristou, Georgios Alexandridis

Abstract: Since their introduction, Kolmogorov-Arnold Networks (KANs) have been successfully applied across several domains, with physics-informed machine learning (PIML) emerging as one of the areas where they have thrived. In the PIML setting, Chebyshev-based physics-informed KANs (cPIKANs) have become the standard due to their computational efficiency. However, like their multilayer perceptron-based counterparts, cPIKANs face significant challenges when scaled to depth, leading to training instabilities that limit their applicability to several PDE problems. To address this, we propose a basis-agnostic, Glorot-like initialization scheme that preserves activation variance and yields substantial improvements in stability and accuracy over the default initialization of cPIKANs. Inspired by the PirateNet architecture, we further introduce Residual-Gated Adaptive KANs (RGA KANs), designed to mitigate divergence in deep cPIKANs where initialization alone is not sufficient. Through empirical tests and information bottleneck analysis, we show that RGA KANs successfully traverse all training phases, unlike baseline cPIKANs, which stagnate in the diffusion phase in specific PDE settings. Evaluations on nine standard forward PDE benchmarks under a fixed training pipeline with adaptive components demonstrate that RGA KANs consistently outperform parameter-matched cPIKANs and PirateNets - often by several orders of magnitude - while remaining stable in settings where the others diverge.

Fully analogue in-memory neural computing via quantum tunneling effect

Authors: Songyuan Li, Teng Wang, Jinrong Tang, Ruiqi Liu, Haoyu Li, Yuyao Lu, Feng Xu, Bin Gao, Can Xie, Xiangwei Zhu

Abstract: Fully analogue neural computation requires hardware that can implement both linear and nonlinear transformations without digital assistance. While analogue in-memory computing efficiently realizes matrix-vector multiplication, the absence of learnable analogue nonlinearities remains a central bottleneck. Here we introduce KANalogue, a fully analogue realization of Kolmogorov-Arnold Networks (KANs) that instantiates univariate basis functions directly using negative-differential-resistance (NDR) devices. By mapping the intrinsic current-voltage characteristics of NDR devices to learnable coordinate-wise nonlinear functions, KANalogue embeds function approximation into device physics while preserving a fully analogue signal path. Using cold-metal tunnel diodes as a representative platform, we construct diverse nonlinear bases and combine them through crossbar-based analogue summation. Experiments on MNIST, FashionMNIST, and CIFAR-10 demonstrate that KANalogue achieves competitive accuracy with substantially fewer parameters and higher crossbar node efficiency than analogue MLPs, while approaching the performance of digital KANs under strict hardware constraints. The framework is not limited to a specific device technology and naturally generalizes to a broad class of NDR devices. These results establish a device-grounded route toward scalable, energy-efficient, fully analogue neural networks.

Physics-Inspired Gaussian Kolmogorov-Arnold Networks for X-ray Scatter Correction in Cone-Beam CT

Authors: Xu Jiang, Huiying Pan, Ligen Shi, Jianing Sun, Wenfeng Xu, Xing Zhao

Abstract: Cone-beam CT (CBCT) employs a flat-panel detector to achieve three-dimensional imaging with high spatial resolution. However, CBCT is susceptible to scatter during data acquisition, which introduces CT value bias and reduced tissue contrast in the reconstructed images, ultimately degrading diagnostic accuracy. To address this issue, we propose a deep learning-based scatter artifact correction method inspired by physical prior knowledge. Leveraging the fact that the observed point scatter probability density distribution exhibits rotational symmetry in the projection domain. The method uses Gaussian Radial Basis Functions (RBF) to model the point scatter function and embeds it into the Kolmogorov-Arnold Networks (KAN) layer, which provides efficient nonlinear mapping capabilities for learning high-dimensional scatter features. By incorporating the physical characteristics of the scattered photon distribution together with the complex function mapping capacity of KAN, the model improves its ability to accurately represent scatter. The effectiveness of the method is validated through both synthetic and real-scan experiments. Experimental results show that the model can effectively correct the scatter artifacts in the reconstructed images and is superior to the current methods in terms of quantitative metrics.

Stiff Circuit System Modeling via Transformer

Authors: Weiman Yan, Yi-Chia Chang, Wanyu Zhao

Abstract: Accurate and efficient circuit behavior modeling is a cornerstone of modern electronic design automation. Among different types of circuits, stiff circuits are challenging to model using previous frameworks. In this work, we propose a new approach using Crossformer, which is a current state-of-the-art Transformer model for time-series prediction tasks, combined with Kolmogorov-Arnold Networks (KANs), to model stiff circuit transient behavior. By leveraging the Crossformer’s temporal representation capabilities and the enhanced feature extraction of KANs, our method achieves improved fidelity in predicting circuit responses to a wide range of input conditions. Experimental evaluations on datasets generated through SPICE simulations of analog-to-digital converter (ADC) circuits demonstrate the effectiveness of our approach, with significant reductions in training time and error rates.

KAN-GCN: Combining Kolmogorov-Arnold Network with Graph Convolution Network for an Accurate Ice Sheet Emulator

Authors: Zesheng Liu, YoungHyun Koo, Maryam Rahnemoonfar

Abstract: We introduce KAN-GCN, a fast and accurate emulator for ice sheet modeling that places a Kolmogorov-Arnold Network (KAN) as a feature-wise calibrator before graph convolution networks (GCNs). The KAN front end applies learnable one-dimensional warps and a linear mixing step, improving feature conditioning and nonlinear encoding without increasing message-passing depth. We employ this architecture to improve the performance of emulators for numerical ice sheet models. Our emulator is trained and tested using 36 melting-rate simulations with 3 mesh-size settings for Pine Island Glacier, Antarctica. Across 2- to 5-layer architectures, KAN-GCN matches or exceeds the accuracy of pure GCN and MLP-GCN baselines. Despite a small parameter overhead, KAN-GCN improves inference throughput on coarser meshes by replacing one edge-wise message-passing layer with a node-wise transform; only the finest mesh shows a modest cost. Overall, KAN-first designs offer a favorable accuracy vs. efficiency trade-off for large transient scenario sweeps.

A Practitioner’s Guide to Kolmogorov-Arnold Networks

Authors: Amir Noorizadegan, Sifan Wang, Leevan Ling, Juan P. Dominguez-Morales

Abstract: Kolmogorov-Arnold Networks (KANs), whose design is inspired-rather than dictated-by the Kolmogorov superposition theorem, have emerged as a structured alternative to MLPs. This review provides a systematic and comprehensive overview of the rapidly expanding KAN literature. The review is organized around three core themes: (i) clarifying the relationships between KANs and Kolmogorov superposition theory (KST), MLPs, and classical kernel methods; (ii) analyzing basis functions as a central design axis; and (iii) summarizing recent advances in accuracy, efficiency, regularization, and convergence. Finally, we provide a practical “Choose-Your-KAN” guide and outline open research challenges and future directions. The accompanying GitHub repository serves as a structured reference for ongoing KAN research.

November

One model to solve them all: 2BSDE families via neural operators

Authors: Takashi Furuya, Anastasis Kratsios, Dylan Possamaï, Bogdan Raonić

Abstract: We introduce a mild generative variant of the classical neural operator model, which leverages Kolmogorov–Arnold networks to solve infinite families of second-order backward stochastic differential equations ($2$BSDEs) on regular bounded Euclidean domains with random terminal time. Our first main result shows that the solution operator associated with a broad range of $2$BSDE families is approximable by appropriate neural operator models. We then identify a structured subclass of (infinite) families of $2$BSDEs whose neural operator approximation requires only a polynomial number of parameters in the reciprocal approximation rate, as opposed to the exponential requirement in general worst-case neural operator guarantees.

CG-FKAN: Compressed-Grid Federated Kolmogorov-Arnold Networks for Communication Constrained Environment

Authors: Seunghun Yu, Youngjoon Lee, Jinu Gong, Joonhyuk Kang

Abstract: Federated learning (FL), widely used in privacy-critical applications, suffers from limited interpretability, whereas Kolmogorov-Arnold Networks (KAN) address this limitation via learnable spline functions. However, existing FL studies applying KAN overlook the communication overhead introduced by grid extension, which is essential for modeling complex functions. In this letter, we propose CG-FKAN, which compresses extended grids by sparsifying and transmitting only essential coefficients under a communication budget. Experiments show that CG-FKAN achieves up to 13.6% lower RMSE than fixed-grid KAN in communication-constrained settings. In addition, we derive a theoretical upper bound on its approximation error.

Interpretable Machine Learning for Reservoir Water Temperatures in the U.S. Red River Basin of the South

Authors: Isabela Suaza-Sierra, Hernan A. Moreno, Luis A De la Fuente, Thomas M. Neeson

Abstract: Accurate prediction of Reservoir Water Temperature (RWT) is vital for sustainable water management, ecosystem health, and climate resilience. Yet, prediction alone offers limited insight into the governing physical processes. To bridge this gap, we integrated explainable machine learning (ML) with symbolic modeling to uncover the drivers of RWT dynamics across ten reservoirs in the Red River Basin, USA, using over 10,000 depth-resolved temperature profiles. We first employed ensemble and neural models, including Random Forest (RF), Extreme Gradient Boosting (XGBoost), and Multilayer Perceptron (MLP), achieving high predictive skill (best RMSE = 1.20 degree Celsius, R^2 = 0.97). Using SHAP (SHapley Additive exPlanations), we quantified the contribution of physical drivers such as air temperature, depth, wind, and lake volume, revealing consistent patterns across reservoirs. To translate these data-driven insights into compact analytical expressions, we developed Kolmogorov Arnold Networks (KANs) to symbolically approximate RWT. Ten progressively complex KAN equations were derived, improving from R^2 = 0.84 using a single predictor (7-day antecedent air temperature) to R^2 = 0.92 with ten predictors, though gains diminished beyond five, highlighting a balance between simplicity and accuracy. The resulting equations, dominated by linear and rational forms, incrementally captured nonlinear behavior while preserving interpretability. Depth consistently emerged as a secondary but critical predictor, whereas precipitation had limited effect. By coupling predictive accuracy with explanatory power, this framework demonstrates how KANs and explainable ML can transform black-box models into transparent surrogates that advance both prediction and understanding of reservoir thermal dynamics.

Hybrid DeepONet Surrogates for Multiphase Flow in Porous Media

Authors: Ezequiel S. Santos, Gabriel F. Barros, Amanda C. N. Oliveira, Rômulo M. Silva, Rodolfo S. M. Freitas, Dakshina M. Valiveti, Xiao-Hui Wu, Fernando A. Rochinha, Alvaro L. G. A. Coutinho

Abstract: The solution of partial differential equations (PDEs) plays a central role in numerous applications in science and engineering, particularly those involving multiphase flow in porous media. Complex, nonlinear systems govern these problems and are notoriously computationally intensive, especially in real-world applications and reservoirs. Recent advances in deep learning have spurred the development of data-driven surrogate models that approximate PDE solutions with reduced computational cost. Among these, Neural Operators such as Fourier Neural Operator (FNO) and Deep Operator Networks (DeepONet) have shown strong potential for learning parameter-to-solution mappings, enabling the generalization across families of PDEs. However, both methods face challenges when applied independently to complex porous media flows, including high memory requirements and difficulty handling the time dimension. To address these limitations, this work introduces hybrid neural operator surrogates based on DeepONet models that integrate Fourier Neural Operators, Multi-Layer Perceptrons (MLPs), and Kolmogorov-Arnold Networks (KANs) within their branch and trunk networks. The proposed framework decouples spatial and temporal learning tasks by splitting these structures into the branch and trunk networks, respectively. We evaluate these hybrid models on multiphase flow in porous media problems ranging in complexity from the steady 2D Darcy flow to the 2D and 3D problems belonging to the $10$th Comparative Solution Project from the Society of Petroleum Engineers. Results demonstrate that hybrid schemes achieve accurate surrogate modeling with significantly fewer parameters while maintaining strong predictive performance on large-scale reservoir simulations.

A Hybrid CNN-Cheby-KAN Framework for Efficient Prediction of Two-Dimensional Airfoil Pressure Distribution

Authors: Yaohong Chen, Luchi Zhang, Yiju Deng, Yanze Yu, Xiang Li, Renshan Jiao

Abstract: The accurate prediction of airfoil pressure distribution is essential for aerodynamic performance evaluation, yet traditional methods such as computational fluid dynamics (CFD) and wind tunnel testing have certain bottlenecks. This paper proposes a hybrid deep learning model combining a Convolutional Neural Network (CNN) and a Chebyshev-enhanced Kolmogorov-Arnold Network (Cheby-KAN) for efficient and accurate prediction of the two-dimensional airfoil flow field. The CNN learns 1549 types of airfoils and encodes airfoil geometries into a compact 16-dimensional feature vector, while the Cheby-KAN models complex nonlinear mappings from flight conditions and spatial coordinates to pressure values. Experiments on multiple airfoils–including RAE2822, NACA0012, e387, and mh38–under various Reynolds numbers and angles of attack demonstrate that the proposed method achieves a mean squared error (MSE) on the order of $10^{-6}$ and a coefficient of determination ($R^2$) exceeding 0.999. The model significantly outperforms traditional Multilayer Perceptrons (MLPs) in accuracy and generalizability, with acceptable computational overhead. These results indicate that the hybrid CNN-Cheby-KAN framework offers a promising data-driven approach for rapid aerodynamic prediction.

KAN-Enhanced Contrastive Learning Accelerating Crystal Structure Identification from XRD Patterns

Authors: Chenlei Xu, Tianhao Su, Jie Xiong, Yue Wu, Shuya Dong, Tian Jiang, Mengwei He, Shuai Chen, Tong-Yi Zhang

Abstract: Accurate determination of crystal structures is central to materials science, underpinning the understanding of composition-structure-property relationships and the discovery of new materials. Powder X-ray diffraction is a key technique in this pursuit due to its versatility and reliability. However, current analysis pipelines still rely heavily on expert knowledge and slow iterative fitting, limiting their scalability in high-throughput and autonomous settings. Here, we introduce a physics-guided contrastive learning framework termed as XCCP. It aligns powder diffraction patterns with candidate crystal structures in a shared embedding space to enable efficient structure retrieval and symmetry recognition. The XRD encoder employs a dual-expert design with a Kolmogorov-Arnold Network projection head, one branch emphasizes low angle reflections reflecting long-range order, while the other captures dense high angle peaks shaped by symmetry. Coupled with a crystal graph encoder, contrastive pretraining yields physically grounded representations. XCCP demonstrates strong performance across tasks, with structure retrieval reaching 0.89 and space group identification attains 0.93 accuracy. The framework further generalizes to compositionally similar multi principal element alloys and demonstrates zero-shot transfer to experimental patterns. These results establish XCCP as a robust, interpretable, and scalable approach that offers a new paradigm for X-ray diffraction analysis. XCCP facilitates high-throughput screening, rapid structural validation and integration into autonomous laboratories.

When Swin Transformer Meets KANs: An Improved Transformer Architecture for Medical Image Segmentation

Authors: Nishchal Sapkota, Haoyan Shi, Yejia Zhang, Xianshi Ma, Bofang Zheng, Fabian Vazquez, Pengfei Gu, Danny Z. Chen

Abstract: Medical image segmentation is critical for accurate diagnostics and treatment planning, but remains challenging due to complex anatomical structures and limited annotated training data. CNN-based segmentation methods excel at local feature extraction, but struggle with modeling long-range dependencies. Transformers, on the other hand, capture global context more effectively, but are inherently data-hungry and computationally expensive. In this work, we introduce UKAST, a U-Net like architecture that integrates rational-function based Kolmogorov-Arnold Networks (KANs) into Swin Transformer encoders. By leveraging rational base functions and Group Rational KANs (GR-KANs) from the Kolmogorov-Arnold Transformer (KAT), our architecture addresses the inefficiencies of vanilla spline-based KANs, yielding a more expressive and data-efficient framework with reduced FLOPs and only a very small increase in parameter count compared to SwinUNETR. UKAST achieves state-of-the-art performance on four diverse 2D and 3D medical image segmentation benchmarks, consistently surpassing both CNN- and Transformer-based baselines. Notably, it attains superior accuracy in data-scarce settings, alleviating the data-hungry limitations of standard Vision Transformers. These results show the potential of KAN-enhanced Transformers to advance data-efficient medical image segmentation. Code is available at: https://github.com/nsapkota417/UKAST

Simplex-FEM Networks (SiFEN): Learning A Triangulated Function Approximator

Authors: Chaymae Yahyati, Ismail Lamaakal, Khalid El Makkaoui, Ibrahim Ouahbi, Yassine Maleh

Abstract: We introduce Simplex-FEM Networks (SiFEN), a learned piecewise-polynomial predictor that represents f: R^d -> R^k as a globally C^r finite-element field on a learned simplicial mesh in an optionally warped input space. Each query activates exactly one simplex and at most d+1 basis functions via barycentric coordinates, yielding explicit locality, controllable smoothness, and cache-friendly sparsity. SiFEN pairs degree-m Bernstein-Bezier polynomials with a light invertible warp and trains end-to-end with shape regularization, semi-discrete OT coverage, and differentiable edge flips. Under standard shape-regularity and bi-Lipschitz warp assumptions, SiFEN achieves the classic FEM approximation rate M^(-m/d) with M mesh vertices. Empirically, on synthetic approximation tasks, tabular regression/classification, and as a drop-in head on compact CNNs, SiFEN matches or surpasses MLPs and KANs at matched parameter budgets, improves calibration (lower ECE/Brier), and reduces inference latency due to geometric locality. These properties make SiFEN a compact, interpretable, and theoretically grounded alternative to dense MLPs and edge-spline networks.

GroupKAN: Efficient Kolmogorov-Arnold Networks via Grouped Spline Modeling

Authors: Guojie Li, Tianyi Liu, Anwar P. P. Abdul Majeed, Muhammad Ateeq, Anh Nguyen, Fan Zhang

Abstract: Medical image segmentation demands models that achieve high accuracy while maintaining computational efficiency and clinical interpretability. While recent Kolmogorov-Arnold Networks (KANs) offer powerful adaptive non-linearities, their full-channel spline transformations incur a quadratic parameter growth of $\mathcal{O}(C^{2}(G+k))$ with respect to the channel dimension $C$, where $G$ and $k$ denote the number of grid intervals and spline polynomial order, respectively. Moreover, unconstrained spline mappings lack structural constraints, leading to excessive functional freedom, which may cause overfitting under limited medical annotations. To address these challenges, we propose GroupKAN (Grouped Kolmogorov-Arnold Networks), an efficient architecture driven by group-structured spline modeling. Specifically, we introduce: (1) Grouped KAN Transform (GKT), which restricts spline interactions to intra-group channel mappings across $g$ groups, effectively reducing the spline-induced quadratic expansion to \textbf{$\mathcal{O}(C^2(\frac{G+k}{g} + 1))$}, thereby significantly lowering the effective quadratic coefficient; and (2) Grouped KAN Activation (GKA), which applies shared spline functions within each group to enable efficient token-wise non-linearities. By imposing structured constraints on channel interactions, GroupKAN achieves a substantial reduction in parameter redundancy without sacrificing expressive capacity.Extensive evaluations on three medical benchmarks (BUSI, GlaS, and CVC) demonstrate that GroupKAN achieves an average IoU of 79.80\%, outperforming the strong U-KAN baseline by +1.11\% while requiring only 47.6\% of the parameters (3.02M vs. 6.35M). Qualitative results further reveal that GroupKAN produces sharply localized activation maps that better align with the ground truth than MLPs and KANs, significantly enhancing clinical interpretability.

An uncertainty-aware physics-informed neural network solution for the Black-Scholes equation: a novel framework for option pricing

Authors: Sina Kazemian, Ghazal Farhani, Amirhessam Yazdi

Abstract: We present an uncertainty-aware, physics-informed neural network (PINN) for option pricing that solves the Black–Scholes (BS) partial differential equation (PDE) as a mesh-free, global surrogate over $(S,t)$. The model embeds the BS operator and boundary/terminal conditions in a residual-based objective and requires no labeled prices. For American options, early exercise is handled via an obstacle-style relaxation while retaining the BS residual in the continuation region. To quantify \emph{epistemic} uncertainty, we introduce an anchored-ensemble fine-tuning stage (AT–PINN) that regularizes each model toward a sampled anchor and yields prediction bands alongside point estimates. On European calls/puts, the approach attains low errors (e.g., MAE $\sim 5\times10^{-2}$, RMSE $\sim 7\times10^{-2}$, explained variance $\approx 0.999$ in representative settings) and tracks ground truth closely across strikes and maturities. For American puts, the method remains accurate (MAE/RMSE on the order of $10^{-1}$ with EV $\approx 0.999$) and does not exhibit the error accumulation associated with time-marching schemes. Against data-driven baselines (ANN, RNN) and a Kolmogorov–Arnold FINN variant (KAN), our PINN matches or outperforms on accuracy while training more stably; anchored ensembles provide uncertainty bands that align with observed error scales. We discuss design choices (loss balancing, sampling near the payoff kink), limitations, and extensions to higher-dimensional BS settings and alternative dynamics.

SFFR: Spatial-Frequency Feature Reconstruction for Multispectral Aerial Object Detection

Authors: Xin Zuo, Chenyu Qu, Haibo Zhan, Jifeng Shen, Wankou Yang

Abstract: Recent multispectral object detection methods have primarily focused on spatial-domain feature fusion based on CNNs or Transformers, while the potential of frequency-domain feature remains underexplored. In this work, we propose a novel Spatial and Frequency Feature Reconstruction method (SFFR) method, which leverages the spatial-frequency feature representation mechanisms of the Kolmogorov-Arnold Network (KAN) to reconstruct complementary representations in both spatial and frequency domains prior to feature fusion. The core components of SFFR are the proposed Frequency Component Exchange KAN (FCEKAN) module and Multi-Scale Gaussian KAN (MSGKAN) module. The FCEKAN introduces an innovative selective frequency component exchange strategy that effectively enhances the complementarity and consistency of cross-modal features based on the frequency feature of RGB and IR images. The MSGKAN module demonstrates excellent nonlinear feature modeling capability in the spatial domain. By leveraging multi-scale Gaussian basis functions, it effectively captures the feature variations caused by scale changes at different UAV flight altitudes, significantly enhancing the model’s adaptability and robustness to scale variations. It is experimentally validated that our proposed FCEKAN and MSGKAN modules are complementary and can effectively capture the frequency and spatial semantic features respectively for better feature fusion. Extensive experiments on the SeaDroneSee, DroneVehicle and DVTOD datasets demonstrate the superior performance and significant advantages of the proposed method in UAV multispectral object perception task. Code will be available at https://github.com/qchenyu1027/SFFR.

Design Principles of Zero-Shot Self-Supervised Unknown Emitter Detectors

Authors: Mikhail Krasnov, Ljupcho Milosheski, Mihael Mohorčič, Carolina Fortuna

Abstract: The proliferation of wireless devices necessitates more robust and reliable emitter detection and identification for critical tasks such as spectrum management and network security. Existing studies exploring methods for unknown emitters identification, however, are typically hindered by their dependence on labeled or proprietary datasets, unrealistic assumptions (e.g. all samples with identical transmitted messages), or deficiency of systematic evaluations across different architectures and design dimensions. In this work, we present a comprehensive evaluation of unknown emitter detection systems across key aspects of the design space, focusing on data modality, learning approaches, and feature learning modules. We demonstrate that prior self-supervised, zero-shot emitter detection approaches commonly use datasets with identical transmitted messages. To address this limitation, we propose a 2D-Constellation data modality for scenarios with varying messages, achieving up to a 40\% performance improvement in ROC-AUC, NMI, and F1 metrics compared to conventional raw I/Q data. Furthermore, we introduce interpretable Kolmogorov-Arnold Networks (KANs) to enhance model transparency, and a Singular Value Decomposition (SVD)-based initialization procedure for feature learning modules operating on sparse 2D-Constellation data, which improves the performance of Deep Clustering approaches by up to 40\% across the same metrics comparing to the modules without SVD initialization. We evaluate all data modalities and learning modules across three learning approaches: Deep Clustering, Auto Encoder and Contrastive Learning.

Kolmogorov-Arnold Chemical Reaction Neural Networks for learning pressure-dependent kinetic rate laws

Authors: Benjamin C. Koenig, Sili Deng

Abstract: Chemical Reaction Neural Networks (CRNNs) have emerged as an interpretable machine learning framework for discovering reaction kinetics directly from data, while strictly adhering to the Arrhenius and mass action laws. However, standard CRNNs cannot represent pressure-dependent or mixture-based rate behavior, which is critical in many combustion and chemical systems and typically requires empirical falloff formulations such as Troe or SRI, or data-based interpolation or polynomial fits such as PLOG or Chebyshev Polynomials. Here, we develop Kolmogorov-Arnold Chemical Reaction Neural Networks (KA-CRNNs) that generalize CRNNs by modeling each kinetic parameter as a learnable function of third-body concentrations using Kolmogorov-Arnold activations. This structure maintains the Arrhenius and mass action interpretability and physical constraints of a vanilla CRNN while enabling assumption-free inference of global and collider-specific pressure effects directly from data. Two proof-of-concept reaction studies are presented to highlight the capability of KA-CRNNs to accurately reproduce pressure-dependent and collider-specific kinetics across a range of temperatures, pressures, and bath gas mixtures, extracting meaningful and generalizable models from sparse training data and significantly outperforming interpolative approaches (2.88x reduction in MSE). The framework establishes a foundation for data-driven discovery of extended kinetic behaviors in complex reacting systems, advancing interpretable and physics-constrained approaches for chemical model inference.

Automatic Grid Updates for Kolmogorov-Arnold Networks using Layer Histograms

Authors: Jamison Moody, James Usevitch

Abstract: Kolmogorov-Arnold Networks (KANs) are a class of neural networks that have received increased attention in recent literature. In contrast to MLPs, KANs leverage parameterized, trainable activation functions and offer several benefits including improved interpretability and higher accuracy on learning symbolic equations. However, the original KAN architecture requires adjustments to the domain discretization of the network (called the “domain grid”) during training, creating extra overhead for the user in the training process. Typical KAN layers are not designed with the ability to autonomously update their domains in a data-driven manner informed by the changing output ranges of previous layers. As an added benefit, this histogram algorithm may also be applied towards detecting out-of-distribution (OOD) inputs in a variety of settings. We demonstrate that AdaptKAN exceeds or matches the performance of prior KAN architectures and MLPs on four different tasks: learning scientific equations from the Feynman dataset, image classification from frozen features, learning a control Lyapunov function, and detecting OOD inputs on the OpenOOD v1.5 benchmark.

Learning Topology-Driven Multi-Subspace Fusion for Grassmannian Deep Network

Authors: Xuan Yu, Tianyang Xu

Abstract: Grassmannian manifold offers a powerful carrier for geometric representation learning by modelling high-dimensional data as low-dimensional subspaces. However, existing approaches predominantly rely on static single-subspace representations, neglecting the dynamic interplay between multiple subspaces critical for capturing complex geometric structures. To address this limitation, we propose a topology-driven multi-subspace fusion framework that enables adaptive subspace collaboration on the Grassmannian. Our solution introduces two key innovations: (1) Inspired by the Kolmogorov-Arnold representation theorem, an adaptive multi-subspace modelling mechanism is proposed that dynamically selects and weights task-relevant subspaces via topological convergence analysis, and (2) a multi-subspace interaction block that fuses heterogeneous geometric representations through Fréchet mean optimisation on the manifold. Theoretically, we establish the convergence guarantees of adaptive subspaces under a projection metric topology, ensuring stable gradient-based optimisation. Practically, we integrate Riemannian batch normalisation and mutual information regularisation to enhance discriminability and robustness. Extensive experiments on 3D action recognition (HDM05, FPHA), EEG classification (MAMEM-SSVEPII), and graph tasks demonstrate state-of-the-art performance. Our work not only advances geometric deep learning but also successfully adapts the proven multi-channel interaction philosophy of Euclidean networks to non-Euclidean domains, achieving superior discriminability and interpretability.

Learning the Basis: A Kolmogorov-Arnold Network Approach Embedding Green’s Function Priors

Authors: Rui Zhu, Yuexing Peng, George C. Alexandropoulos, Wenbo Wang, Wei Xiang

Abstract: The Method of Moments (MoM) is constrained by the usage of static, geometry-defined basis functions, such as the Rao-Wilton-Glisson (RWG) basis. This letter reframes electromagnetic modeling around a learnable basis representation rather than solving for the coefficients over a fixed basis. We first show that the RWG basis is essentially a static and piecewise-linear realization of the Kolmogorov-Arnold representation theorem. Inspired by this insight, we propose PhyKAN, a physics-informed Kolmogorov-Arnold Network (KAN) that generalizes RWG into a learnable and adaptive basis family. Derived from the EFIE, PhyKAN integrates a local KAN branch with a global branch embedded with Green’s function priors to preserve physical consistency. It is demonstrated that, across canonical geometries, PhyKAN achieves sub-0.01 reconstruction errors as well as accurate, unsupervised radar cross section predictions, offering an interpretable, physics-consistent bridge between classical solvers and modern neural network models for electromagnetic modeling.

Adaptive graph Kolmogorov-Arnold network for 3D human pose estimation

Authors: Abu Taib Mohammed Shahjahan, A. Ben Hamza

Abstract: Graph convolutional network (GCN)-based methods have shown strong performance in 3D human pose estimation by leveraging the natural graph structure of the human skeleton. However, their local receptive field limits their ability to capture long-range dependencies essential for handling occlusions and depth ambiguities. They also exhibit spectral bias, which prioritizes low-frequency components while struggling to model high-frequency details. In this paper, we introduce PoseKAN, an adaptive graph Kolmogorov-Arnold Network (KAN), framework that extends KANs to graph-based learning for 2D-to-3D pose lifting from a single image. Unlike GCNs that use fixed activation functions, KANs employ learnable functions on graph edges, allowing data-driven, adaptive feature transformations. This enhances the model’s adaptability and expressiveness, making it more expressive in learning complex pose variations. Our model employs multi-hop feature aggregation, ensuring the body joints can leverage information from both local and distant neighbors, leading to improved spatial awareness. It also incorporates residual PoseKAN blocks for deeper feature refinement, and a global response normalization for improved feature selectivity and contrast. Extensive experiments on benchmark datasets demonstrate the competitive performance of our model against state-of-the-art methods.

Physics-informed Machine Learning for Static Friction Modeling in Robotic Manipulators Based on Kolmogorov-Arnold Networks

Authors: Yizheng Wang, Timon Rabczuk, Yinghua Liu

Abstract: Friction modeling plays a crucial role in achieving high-precision motion control in robotic operating systems. Traditional static friction models (such as the Stribeck model) are widely used due to their simple forms; however, they typically require predefined functional assumptions, which poses significant challenges when dealing with unknown functional structures. To address this issue, this paper proposes a physics-inspired machine learning approach based on the Kolmogorov Arnold Network (KAN) for static friction modeling of robotic joints. The method integrates spline activation functions with a symbolic regression mechanism, enabling model simplification and physical expression extraction through pruning and attribute scoring, while maintaining both high prediction accuracy and interpretability. We first validate the method’s capability to accurately identify key parameters under known functional models, and further demonstrate its robustness and generalization ability under conditions with unknown functional structures and noisy data. Experiments conducted on both synthetic data and real friction data collected from a six-degree-of-freedom industrial manipulator show that the proposed method achieves a coefficient of determination greater than 0.95 across various tasks and successfully extracts concise and physically meaningful friction expressions. This study provides a new perspective for interpretable and data-driven robotic friction modeling with promising engineering applicability.

The modified Physics-Informed Hybrid Parallel Kolmogorov–Arnold and Multilayer Perceptron Architecture with domain decomposition

Authors: Qiumei Huang, Xu Wang, Yu Zhao

Abstract: In this work, we propose a modified Hybrid Parallel Kolmogorov–Arnold Network and Multilayer Perceptron Physics-Informed Neural Network to overcome the high-frequency and multiscale challenges inherent in Physics-Informed Neural Networks. This proposed model features a trainable weighting parameter to optimize the convex combination of outputs from the Kolmogorov–Arnold Network and the Multilayer Perceptron, thus maximizing the networks’ capabilities to capture different frequency components. Furthermore, we adopt an overlapping domain decomposition technique to decompose complex problems into subproblems, which alleviates the challenge of global optimization. Benchmark results demonstrate that our method reduces training costs and improves computational efficiency compared with manual hyperparameter tuning in solving high-frequency multiscale problems.

GROVER: Graph-guided Representation of Omics and Vision with Expert Regulation for Adaptive Spatial Multi-omics Fusion

Authors: Yongjun Xiao, Dian Meng, Xinlei Huang, Yanran Liu, Shiwei Ruan, Ziyue Qiao, Xubin Zheng

Abstract: Effectively modeling multimodal spatial omics data is critical for understanding tissue complexity and underlying biological mechanisms. While spatial transcriptomics, proteomics, and epigenomics capture molecular features, they lack pathological morphological context. Integrating these omics with histopathological images is therefore essential for comprehensive disease tissue analysis. However, substantial heterogeneity across omics, imaging, and spatial modalities poses significant challenges. Naive fusion of semantically distinct sources often leads to ambiguous representations. Additionally, the resolution mismatch between high-resolution histology images and lower-resolution sequencing spots complicates spatial alignment. Biological perturbations during sample preparation further distort modality-specific signals, hindering accurate integration. To address these challenges, we propose Graph-guided Representation of Omics and Vision with Expert Regulation for Adaptive Spatial Multi-omics Fusion (GROVER), a novel framework for adaptive integration of spatial multi-omics data. GROVER leverages a Graph Convolutional Network encoder based on Kolmogorov-Arnold Networks to capture the nonlinear dependencies between each modality and its associated spatial structure, thereby producing expressive, modality-specific embeddings. To align these representations, we introduce a spot-feature-pair contrastive learning strategy that explicitly optimizes the correspondence across modalities at each spot. Furthermore, we design a dynamic expert routing mechanism that adaptively selects informative modalities for each spot while suppressing noisy or low-quality inputs. Experiments on real-world spatial omics datasets demonstrate that GROVER outperforms state-of-the-art baselines, providing a robust and reliable solution for multimodal integration.

KAN/H: Kolmogorov-Arnold Network using Haar-like bases

Author: Susumu Katayama

Abstract: Function approximation using Haar basis systems offers an efficient implementation when compressed via Patricia trees while retaining the flexibility of wavelets for both global and local fitting. However, like B-spline-based approximations, achieving high accuracy in high dimensions remains challenging. This paper proposes KAN/H, a variant of the Kolmogorov-Arnold Network (KAN) that uses a Haar-like hierarchical basis system with nonzero first-order derivatives, instead of B-splines. We also propose a learning-rate scheduling method and a method for handling unbounded real-valued inputs, leveraging properties of linear approximation with Haar-like hierarchical bases. By applying the resulting algorithm to function-approximation problems and MNIST, we confirm that our approach requires minimal problem-specific hyperparameter tuning.

Learning Fair Representations with Kolmogorov-Arnold Networks

Authors: Amisha Priyadarshini, Sergio Gago-Masague

Abstract: Despite recent advances in fairness-aware machine learning, predictive models often exhibit discriminatory behavior towards marginalized groups. Such unfairness might arise from biased training data, model design, or representational disparities across groups, posing significant challenges in high-stakes decision-making domains such as college admissions. While existing fair learning models aim to mitigate bias, achieving an optimal trade-off between fairness and accuracy remains a challenge. Moreover, the reliance on black-box models hinders interpretability, limiting their applicability in socially sensitive domains. To circumvent these issues, we propose integrating Kolmogorov-Arnold Networks (KANs) within a fair adversarial learning framework. Leveraging the adversarial robustness and interpretability of KANs, our approach facilitates stable adversarial learning. We derive theoretical insights into the spline-based KAN architecture that ensure stability during adversarial optimization. Additionally, an adaptive fairness penalty update mechanism is proposed to strike a balance between fairness and accuracy. We back these findings with empirical evidence on two real-world admissions datasets, demonstrating the proposed framework’s efficiency in achieving fairness across sensitive attributes while preserving predictive performance.

Catastrophic Forgetting in Kolmogorov-Arnold Networks

Authors: Mohammad Marufur Rahman, Guanchu Wang, Kaixiong Zhou, Minghan Chen, Fan Yang

Abstract: Catastrophic forgetting is a longstanding challenge in continual learning, where models lose knowledge from earlier tasks when learning new ones. While various mitigation strategies have been proposed for Multi-Layer Perceptrons (MLPs), recent architectural advances like Kolmogorov-Arnold Networks (KANs) have been suggested to offer intrinsic resistance to forgetting by leveraging localized spline-based activations. However, the practical behavior of KANs under continual learning remains unclear, and their limitations are not well understood. To address this, we present a comprehensive study of catastrophic forgetting in KANs and develop a theoretical framework that links forgetting to activation support overlap and intrinsic data dimension. We validate these analyses through systematic experiments on synthetic and vision tasks, measuring forgetting dynamics under varying model configurations and data complexity. Further, we introduce KAN-LoRA, a novel adapter design for parameter-efficient continual fine-tuning of language models, and evaluate its effectiveness in knowledge editing tasks. Our findings reveal that while KANs exhibit promising retention in low-dimensional algorithmic settings, they remain vulnerable to forgetting in high-dimensional domains such as image classification and language modeling. These results advance the understanding of KANs’ strengths and limitations, offering practical insights for continual learning system design.

KANGURA: Kolmogorov-Arnold Network-Based Geometry-Aware Learning with Unified Representation Attention for 3D Modeling of Complex Structures

Authors: Mohammad Reza Shafie, Morteza Hajiabadi, Hamed Khosravi, Mobina Noori, Imtiaz Ahmed

Abstract: Microbial Fuel Cells (MFCs) offer a promising pathway for sustainable energy generation by converting organic matter into electricity through microbial processes. A key factor influencing MFC performance is the anode structure, where design and material properties play a crucial role. Existing predictive models struggle to capture the complex geometric dependencies necessary to optimize these structures. To solve this problem, we propose KANGURA: Kolmogorov-Arnold Network-Based Geometry-Aware Learning with Unified Representation Attention. KANGURA introduces a new approach to three-dimensional (3D) machine learning modeling. It formulates prediction as a function decomposition problem, where Kolmogorov-Arnold Network (KAN)- based representation learning reconstructs geometric relationships without a conventional multi- layer perceptron (MLP). To refine spatial understanding, geometry-disentangled representation learning separates structural variations into interpretable components, while unified attention mechanisms dynamically enhance critical geometric regions. Experimental results demonstrate that KANGURA outperforms over 15 state-of-the-art (SOTA) models on the ModelNet40 benchmark dataset, achieving 92.7% accuracy, and excels in a real-world MFC anode structure problem with 97% accuracy. This establishes KANGURA as a robust framework for 3D geometric modeling, unlocking new possibilities for optimizing complex structures in advanced manufacturing and quality-driven engineering applications.

PolyKAN: Efficient Fused GPU Operators for Polynomial Kolmogorov-Arnold Network Variants

Authors: Mingkun Yu, Heming Zhong, Dan Huang, Yutong Lu, Jiazhi Jiang

Abstract: Kolmogorov-Arnold Networks (KANs) promise higher expressive capability and stronger interpretability than Multi-Layer Perceptron, particularly in the domain of AI for Science. However, practical adoption has been hindered by low GPU utilization of existing parallel implementations. To address this challenge, we present a GPU-accelerated operator library, named PolyKAN which is the first general open-source implementation of KAN and its variants. PolyKAN fuses the forward and backward passes of polynomial KAN layers into a concise set of optimized CUDA kernels. Four orthogonal techniques underpin the design: (i) \emph{lookup-table} with linear interpolation that replaces runtime expensive math-library functions; (ii) \emph{2D tiling} to expose thread-level parallelism with preserving memory locality; (iii) a \emph{two-stage reduction} scheme converting scattered atomic updates into a single controllable merge step; and (iv) \emph{coefficient-layout reordering} yielding unit-stride reads under the tiled schedule. Using a KAN variant, Chebyshev KAN, as a case-study, PolyKAN delivers $1.2$–$10\times$ faster inference and $1.4$–$12\times$ faster training than a Triton + cuBLAS baseline, with identical accuracy on speech, audio-enhancement, and tabular-regression workloads on both highend GPU and consumer-grade GPU.

An Interpretable Federated Learning Control Framework Design for Smart Grid Resilience

Authors: Ibrahim Shahbaz, Eman Hammad, Abdallah Farraj

Abstract: Power systems remain highly vulnerable to disturbances and cyber-attacks, underscoring the need for resilient and adaptive control strategies. In this work, we investigate a data-driven Federated Learning Control (FLC) framework for transient stability resilience under cyber-physical disturbances. The FLC employs interpretable neural controllers based on the Chebyshev Kolmogorov-Arnold Network (ChebyKAN), trained on a shared centralized control policy and deployed for distributed execution. Simulation results on the IEEE 39-bus New England system show that the proposed FLC consistently achieves faster stabilization than distributed baselines at moderate control levels (10\%–60\%), highlighting its potential as a scalable, resilient, and interpretable learning-based control solution for modern power grids.

Fourier-KAN-Mamba: A Novel State-Space Equation Approach for Time-Series Anomaly Detection

Authors: Xiancheng Wang, Lin Wang, Rui Wang, Zhibo Zhang, Minghang Zhao

Abstract: Time-series anomaly detection plays a critical role in numerous real-world applications, including industrial monitoring and fault diagnosis. Recently, Mamba-based state-space models have shown remarkable efficiency in long-sequence modeling. However, directly applying Mamba to anomaly detection tasks still faces challenges in capturing complex temporal patterns and nonlinear dynamics. In this paper, we propose Fourier-KAN-Mamba, a novel hybrid architecture that integrates Fourier layer, Kolmogorov-Arnold Networks (KAN), and Mamba selective state-space model. The Fourier layer extracts multi-scale frequency features, KAN enhances nonlinear representation capability, and a temporal gating control mechanism further improves the model’s ability to distinguish normal and anomalous patterns. Extensive experiments on MSL, SMAP, and SWaT datasets demonstrate that our method significantly outperforms existing state-of-the-art approaches. Keywords: time-series anomaly detection, state-space model, Mamba, Fourier transform, Kolmogorov-Arnold Network △ Less

Addressing the gravitational collapse of a massless scalar field with Physics-Informed Neural Networks

Authors: Antonio Ferrer-Sánchez, Nino Villanueva-Espinosa, Carlos Hernani Morales, Roberto Ruiz de Austri-Bazan, José A. Font, José David Martín-Guerrero, Matthew W. Choptuik

Abstract: The gravitational collapse of a massless scalar field remains a demanding benchmark for numerical methods in numerical relativity, as it exhibits critical behavior at the boundary between dispersion and black hole formation. In this work we revisit this problem by relying on Physics-Informed Neural Networks (PINNs) as flexible solvers for partial differential equations, thereby providing a comparative assessment of several recent neural architectures. Building on the Einstein-massless-Klein-Gordon formulation in polar-areal coordinates, we consider four initial-value problems encompassing subcritical, critical, and supercritical regimes and use high-resolution finite-difference simulations as reference solutions. Our study is primarily comparative: we evaluate several state-of-the-art deep learning architectures, including vanilla and high-precision PINNs, sinusoidal-feature and quadratic-residual variants, and Kolmogorov-Arnold Networks, all trained under a common loss design that encodes the field equations, boundary conditions, and causal time-space enforcement, together with a novel adaptive spacetime sampling. Within this framework we also introduce ModPINN, a modest modification of standard PINNs that augments standard multilayer perceptrons with coordinate embeddings, quadratic layers, and other common ingredients in recent literature. This study shows that deep-learning-based methods can reproduce finite-difference solutions for the scalar field and the spacetime metric with competitive accuracy using significantly fewer collocation points than more traditional methodologies. While no single architecture dominates in all regimes, ModPINN achieves particularly stable and accurate solutions near criticality, indicating that suitably designed embeddings and adaptive sampling can enhance the robustness of PINNs for challenging gravitational-collapse scenarios.

RadioKMoE: Knowledge-Guided Radiomap Estimation with Kolmogorov-Arnold Networks and Mixture-of-Experts

Authors: Fupei Guo, Kerry Pan, Songyang Zhang, Yue Wang, Zhi Ding

Abstract: Radiomap serves as a vital tool for wireless network management and deployment by providing powerful spatial knowledge of signal propagation and coverage. However, increasingly complex radio propagation behavior and surrounding environments pose strong challenges for radiomap estimation (RME). In this work, we propose a knowledge-guided RME framework that integrates Kolmogorov-Arnold Networks (KAN) with Mixture-of-Experts (MoE), namely RadioKMoE. Specifically, we design a KAN module to predict an initial coarse coverage map, leveraging KAN’s strength in approximating physics models and global radio propagation patterns. The initial coarse map, together with environmental information, drives our MoE network for precise radiomap estimation. Unlike conventional deep learning models, the MoE module comprises expert networks specializing in distinct radiomap patterns to improve local details while preserving global consistency. Experimental results in both multi- and single-band RME demonstrate the enhanced accuracy and robustness of the proposed RadioKMoE in radiomap estimation.

Scaling Implicit Fields via Hypernetwork-Driven Multiscale Coordinate Transformations

Author: Plein Versace

Abstract: Implicit Neural Representations (INRs) have emerged as a powerful paradigm for representing signals such as images, 3D shapes, signed distance fields, and radiance fields. While significant progress has been made in architecture design (e.g., SIREN, FFC, KAN-based INRs) and optimization strategies (meta-learning, amortization, distillation), existing approaches still suffer from two core limitations: (1) a representation bottleneck that forces a single MLP to uniformly model heterogeneous local structures, and (2) limited scalability due to the absence of a hierarchical mechanism that dynamically adapts to signal complexity. This work introduces Hyper-Coordinate Implicit Neural Representations (HC-INR), a new class of INRs that break the representational bottleneck by learning signal-adaptive coordinate transformations using a hypernetwork. HC-INR decomposes the representation task into two components: (i) a learned multiscale coordinate transformation module that warps the input domain into a disentangled latent space, and (ii) a compact implicit field network that models the transformed signal with significantly reduced complexity. The proposed model introduces a hierarchical hypernetwork architecture that conditions coordinate transformations on local signal features, enabling dynamic allocation of representation capacity. We theoretically show that HC-INR strictly increases the upper bound of representable frequency bands while maintaining Lipschitz stability. Extensive experiments across image fitting, shape reconstruction, and neural radiance field approximation demonstrate that HC-INR achieves up to 4 times higher reconstruction fidelity than strong INR baselines while using 30–60\% fewer parameters.

DE-KAN: A Kolmogorov Arnold Network with Dual Encoder for accurate 2D Teeth Segmentation

Authors: Md Mizanur Rahman Mustakim, Jianwu Li, Sumya Bhuiyan, Mohammad Mehedi Hasan, Bing Han

Abstract: Accurate segmentation of individual teeth from panoramic radiographs remains a challenging task due to anatomical variations, irregular tooth shapes, and overlapping structures. These complexities often limit the performance of conventional deep learning models. To address this, we propose DE-KAN, a novel Dual Encoder Kolmogorov Arnold Network, which enhances feature representation and segmentation precision. The framework employs a ResNet-18 encoder for augmented inputs and a customized CNN encoder for original inputs, enabling the complementary extraction of global and local spatial features. These features are fused through KAN-based bottleneck layers, incorporating nonlinear learnable activation functions derived from the Kolmogorov Arnold representation theorem to improve learning capacity and interpretability. Extensive experiments on two benchmark dental X-ray datasets demonstrate that DE-KAN outperforms state-of-the-art segmentation models, achieving mIoU of 94.5%, Dice coefficient of 97.1%, accuracy of 98.91%, and recall of 97.36%, representing up to +4.7% improvement in Dice compared to existing methods.

KAN vs LSTM Performance in Time Series Forecasting

Authors: Tabish Ali Rather, S M Mahmudul Hasan Joy, Nadezda Sukhorukova, Federico Frascoli

Abstract: This paper compares Kolmogorov-Arnold Networks (KAN) and Long Short-Term Memory networks (LSTM) for forecasting non-deterministic stock price data, evaluating predictive accuracy versus interpretability trade-offs using Root Mean Square Error (RMSE).LSTM demonstrates substantial superiority across all tested prediction horizons, confirming their established effectiveness for sequential data modelling. Standard KAN, while offering theoretical interpretability through the Kolmogorov-Arnold representation theorem, exhibits significantly higher error rates and limited practical applicability for time series forecasting. The results confirm LSTM dominance in accuracy-critical time series applications while identifying computational efficiency as KANs’ primary advantage in resource-constrained scenarios where accuracy requirements are less stringent. The findings support LSTM adoption for practical financial forecasting while suggesting that continued research into specialised KAN architectures may yield future improvements.

QuantKAN: A Unified Quantization Framework for Kolmogorov Arnold Networks

Authors: Kazi Ahmed Asif Fuad, Lizhong Chen

Abstract: Kolmogorov Arnold Networks (KANs) represent a new class of neural architectures that replace conventional linear transformations and node-based nonlinearities with spline-based function approximations distributed along network edges. Although KANs offer strong expressivity and interpretability, their heterogeneous spline and base branch parameters hinder efficient quantization, which remains unexamined compared to CNNs and Transformers. In this paper, we present QuantKAN, a unified framework for quantizing KANs across both quantization aware training (QAT) and post-training quantization (PTQ) regimes. QuantKAN extends modern quantization algorithms, such as LSQ, LSQ+, PACT, DoReFa, QIL, GPTQ, BRECQ, AdaRound, AWQ, and HAWQ-V2, to spline based layers with branch-specific quantizers for base, spline, and activation components. Through extensive experiments on MNIST, CIFAR 10, and CIFAR 100 across multiple KAN variants (EfficientKAN, FastKAN, PyKAN, and KAGN), we establish the first systematic benchmarks for low-bit spline networks. Our results show that KANs, particularly deeper KAGN variants, are compatible with low-bit quantization but exhibit strong method architecture interactions: LSQ, LSQ+, and PACT preserve near full precision accuracy at 4 bit for shallow KAN MLP and ConvNet models, while DoReFa provides the most stable behavior for deeper KAGN under aggressive low-bit settings. For PTQ, GPTQ and Uniform consistently deliver the strongest overall performance across datasets, with BRECQ highly competitive on simpler regimes such as MNIST. Our proposed QuantKAN framework thus unifies spline learning and quantization, and provides practical tools and guidelines for efficiently deploying KANs in real-world, resource-constrained environments.

WaveTuner: Comprehensive Wavelet Subband Tuning for Time Series Forecasting

Authors: Yubo Wang, Hui He, Chaoxi Niu, Zhendong Niu

Abstract: Due to the inherent complexity, temporal patterns in real-world time series often evolve across multiple intertwined scales, including long-term periodicity, short-term fluctuations, and abrupt regime shifts. While existing literature has designed many sophisticated decomposition approaches based on the time or frequency domain to partition trend-seasonality components and high-low frequency components, an alternative line of approaches based on the wavelet domain has been proposed to provide a unified multi-resolution representation with precise time-frequency localization. However, most wavelet-based methods suffer from a persistent bias toward recursively decomposing only low-frequency components, severely underutilizing subtle yet informative high-frequency components that are pivotal for precise time series forecasting. To address this problem, we propose WaveTuner, a Wavelet decomposition framework empowered by full-spectrum subband Tuning for time series forecasting. Concretely, WaveTuner comprises two key modules: (i) Adaptive Wavelet Refinement module, that transforms time series into time-frequency coefficients, utilizes an adaptive router to dynamically assign subband weights, and generates subband-specific embeddings to support refinement; and (ii) Multi-Branch Specialization module, that employs multiple functional branches, each instantiated as a flexible Kolmogorov-Arnold Network (KAN) with a distinct functional order to model a specific spectral subband. Equipped with these modules, WaveTuner comprehensively tunes global trends and local variations within a unified time-frequency framework. Extensive experiments on eight real-world datasets demonstrate WaveTuner achieves state-of-the-art forecasting performance in time series forecasting.

Physics-informed Neural Operator Learning for Nonlinear Grad-Shafranov Equation

Authors: Siqi Ding, Zitong Zhang, Guoyang Shi, Xingyu Li, Xiang Gu, Yanan Xu, Huasheng Xie, Hanyue Zhao, Yuejiang Shi, Tianyuan Liu

Abstract: As artificial intelligence emerges as a transformative enabler for fusion energy commercialization, fast and accurate solvers become increasingly critical. In magnetic confinement nuclear fusion, rapid and accurate solution of the Grad-Shafranov equation (GSE) is essential for real-time plasma control and analysis. Traditional numerical solvers achieve high precision but are computationally prohibitive, while data-driven surrogates infer quickly but fail to enforce physical laws and generalize poorly beyond training distributions. To address this challenge, we present a Physics-Informed Neural Operator (PINO) that directly learns the GSE solution operator, mapping shape parameters of last closed flux surface to equilibrium solutions for realistic nonlinear current profiles. Comprehensive benchmarking of five neural architectures identifies the novel Transformer-KAN (Kolmogorov-Arnold Network) Neural Operator (TKNO) as achieving highest accuracy (0.25% mean L2 relative error) under supervised training (only data-driven). However, all data-driven models exhibit large physics residuals, indicating poor physical consistency. Our unsupervised training can reduce the residuals by nearly four orders of magnitude through embedding physics-based loss terms without labeled data. Critically, semi-supervised learning–integrating sparse labeled data (100 interior points) with physics constraints–achieves optimal balance: 0.48% interpolation error and the most robust extrapolation performance (4.76% error, 8.9x degradation factor vs 39.8x for supervised models). Accelerated by TensorRT optimization, our models enable millisecond-level inference, establishing PINO as a promising pathway for next-generation fusion control systems.

Enhancing Burmese News Classification with Kolmogorov-Arnold Network Head Fine-tuning

Authors: Thura Aung, Eaint Kay Khaing Kyaw, Ye Kyaw Thu, Thazin Myint Oo, Thepchai Supnithi

Abstract: In low-resource languages like Burmese, classification tasks often fine-tune only the final classification layer, keeping pre-trained encoder weights frozen. While Multi-Layer Perceptrons (MLPs) are commonly used, their fixed non-linearity can limit expressiveness and increase computational cost. This work explores Kolmogorov-Arnold Networks (KANs) as alternative classification heads, evaluating Fourier-based FourierKAN, Spline-based EfficientKAN, and Grid-based FasterKAN-across diverse embeddings including TF-IDF, fastText, and multilingual transformers (mBERT, Distil-mBERT). Experimental results show that KAN-based heads are competitive with or superior to MLPs. EfficientKAN with fastText achieved the highest F1-score (0.928), while FasterKAN offered the best trade-off between speed and accuracy. On transformer embeddings, EfficientKAN matched or slightly outperformed MLPs with mBERT (0.917 F1). These findings highlight KANs as expressive, efficient alternatives to MLPs for low-resource language classification.

SUPN: Shallow Universal Polynomial Networks

Authors: Zachary Morrow, Michael Penwarden, Brian Chen, Aurya Javeed, Akil Narayan, John D. Jakeman

Abstract: Deep neural networks (DNNs) and Kolmogorov-Arnold networks (KANs) are popular methods for function approximation due to their flexibility and expressivity. However, they typically require a large number of trainable parameters to produce a suitable approximation. Beyond making the resulting network less transparent, overparameterization creates a large optimization space, likely producing local minima in training that have quite different generalization errors. In this case, network initialization can have an outsize impact on the model’s out-of-sample accuracy. For these reasons, we propose shallow universal polynomial networks (SUPNs). These networks replace all but the last hidden layer with a single layer of polynomials with learnable coefficients, leveraging the strengths of DNNs and polynomials to achieve sufficient expressivity with far fewer parameters. We prove that SUPNs converge at the same rate as the best polynomial approximation of the same degree, and we derive explicit formulas for quasi-optimal SUPN parameters. We complement theory with an extensive suite of numerical experiments involving SUPNs, DNNs, KANs, and polynomial projection in one, two, and ten dimensions, consisting of over 13,000 trained models. On the target functions we numerically studied, for a given number of trainable parameters, the approximation error and variability are often lower for SUPNs than for DNNs and KANs by an order of magnitude. In our examples, SUPNs even outperform polynomial projection on non-smooth functions.

Scale-Agnostic Kolmogorov-Arnold Geometry in Neural Networks

Authors: Mathew Vanherreweghe, Michael H. Freedman, Keith M. Adams

Abstract: Recent work by Freedman and Mulligan demonstrated that shallow multilayer perceptrons spontaneously develop Kolmogorov-Arnold geometric (KAG) structure during training on synthetic three-dimensional tasks. However, it remained unclear whether this phenomenon persists in realistic high-dimensional settings and what spatial properties this geometry exhibits. We extend KAG analysis to MNIST digit classification (784 dimensions) using 2-layer MLPs with systematic spatial analysis at multiple scales. We find that KAG emerges during training and appears consistently across spatial scales, from local 7-pixel neighborhoods to the full 28x28 image. This scale-agnostic property holds across different training procedures: both standard training and training with spatial augmentation produce the same qualitative pattern. These findings reveal that neural networks spontaneously develop organized, scale-invariant geometric structure during learning on realistic high-dimensional data.

AdS/Deep-Learning made easy II: neural network-based approaches to holography and inverse problems

Authors: Hyun-Sik Jeong, Hanse Kim, Keun-Young Kim, Gaya Yun, Hyeonwoo Yu, Kwan Yun

Abstract: We apply physics-informed machine learning (PIML) to solve inverse problems in holography and classical mechanics, focusing on neural ordinary differential equations (Neural ODEs) and physics-informed neural networks (PINNs) for solving non-linear differential equations of motion. First, we introduce holographic inverse problems and demonstrate how PIML can reconstruct bulk spacetime and effective potentials from boundary quantum data. To illustrate this, two case studies are explored: the QCD equation of state in holographic QCD and $T$-linear resistivity in holographic strange metals. Additionally, we explicitly show how such holographic problems can be analogized to inverse problems in classical mechanics, modeling frictional forces with neural networks. We also explore Kolmogorov-Arnold Networks (KANs) as an alternative to traditional neural networks, offering more efficient solutions in certain cases. This manuscript aim to provide a systematic framework for using neural networks in inverse problems, serving as a comprehensive reference for researchers in machine learning for high-energy physics, with methodologies that also have broader applications in mathematics, engineering, and the natural sciences.

Multi-Modal Scene Graph with Kolmogorov-Arnold Experts for Audio-Visual Question Answering

Authors: Zijian Fu, Changsheng Lv, Mengshi Qi, Huadong Ma

Abstract: In this paper, we propose a novel Multi-Modal Scene Graph with Kolmogorov-Arnold Expert Network for Audio-Visual Question Answering (SHRIKE). The task aims to mimic human reasoning by extracting and fusing information from audio-visual scenes, with the main challenge being the identification of question-relevant cues from the complex audio-visual content. Existing methods fail to capture the structural information within video, and suffer from insufficient fine-grained modeling of multi-modal features. To address these issues, we are the first to introduce a new multi-modal scene graph that explicitly models the objects and their relationship as a visually grounded, structured representation of the audio-visual scene. Furthermore, we design a Kolmogorov-Arnold Network~(KAN)-based Mixture of Experts (MoE) to enhance the expressive power of the temporal integration stage. This enables more fine-grained modeling of cross-modal interactions within the question-aware fused audio-visual representation, leading to capture richer and more nuanced patterns and then improve temporal reasoning performance. We evaluate the model on the established MUSIC-AVQA and MUSIC-AVQA v2 benchmarks, where it achieves state-of-the-art performance. Code and model checkpoints will be publicly released.

December

KAN-SAs: Efficient Acceleration of Kolmogorov-Arnold Networks on Systolic Arrays

Authors: Sohaib Errabii, Olivier Sentieys, Marcello Traiola

Abstract: Kolmogorov-Arnold Networks (KANs) have garnered significant attention for their promise of improved parameter efficiency and explainability compared to traditional Deep Neural Networks (DNNs). KANs’ key innovation lies in the use of learnable non-linear activation functions, which are parametrized as splines. Splines are expressed as a linear combination of basis functions (B-splines). B-splines prove particularly challenging to accelerate due to their recursive definition. Systolic Array (SA)based architectures have shown great promise as DNN accelerators thanks to their energy efficiency and low latency. However, their suitability and efficiency in accelerating KANs have never been assessed. Thus, in this work, we explore the use of SA architecture to accelerate the KAN inference. We show that, while SAs can be used to accelerate part of the KAN inference, their utilization can be reduced to 30%. Hence, we propose KAN-SAs, a novel SA-based accelerator that leverages intrinsic properties of B-splines to enable efficient KAN inference. By including a nonrecursive B-spline implementation and leveraging the intrinsic KAN sparsity, KAN-SAs enhances conventional SAs, enabling efficient KAN inference, in addition to conventional DNNs. KAN-SAs achieves up to 100% SA utilization and up to 50% clock cycles reduction compared to conventional SAs of equivalent area, as shown by hardware synthesis results on a 28nm FD-SOI technology. We also evaluate different configurations of the accelerator on various KAN applications, confirming the improved efficiency of KAN inference provided by KAN-SAs.

Scalable and Interpretable Scientific Discovery via Sparse Variational Gaussian Process Kolmogorov-Arnold Networks (SVGP KAN)

Author: Y. Sungtaek Ju

Abstract: Kolmogorov-Arnold Networks (KANs) offer a promising alternative to Multi-Layer Perceptron (MLP) by placing learnable univariate functions on network edges, enhancing interpretability. However, standard KANs lack probabilistic outputs, limiting their utility in applications requiring uncertainty quantification. While recent Gaussian Process (GP) extensions to KANs address this, they utilize exact inference methods that scale cubically with data size N, restricting their application to smaller datasets. We introduce the Sparse Variational GP-KAN (SVGP-KAN), an architecture that integrates sparse variational inference with the KAN topology. By employing $M$ inducing points and analytic moment matching, our method reduces computational complexity from $O(N^3)$ to $O(NM^2)$ or linear in sample size, enabling the application of probabilistic KANs to larger scientific datasets. Furthermore, we demonstrate that integrating a permutation-based importance analysis enables the network to function as a framework for structural identification, identifying relevant inputs and classifying functional relationships.

DB-KAUNet: An Adaptive Dual Branch Kolmogorov-Arnold UNet for Retinal Vessel Segmentation

Authors: Hongyu Xu, Panpan Meng, Meng Wang, Dayu Hu, Liming Liang, Xiaoqi Sheng

Abstract: Accurate segmentation of retinal vessels is crucial for the clinical diagnosis of numerous ophthalmic and systemic diseases. However, traditional Convolutional Neural Network (CNN) methods exhibit inherent limitations, struggling to capture long-range dependencies and complex nonlinear relationships. To address the above limitations, an Adaptive Dual Branch Kolmogorov-Arnold UNet (DB-KAUNet) is proposed for retinal vessel segmentation. In DB-KAUNet, we design a Heterogeneous Dual-Branch Encoder (HDBE) that features parallel CNN and Transformer pathways. The HDBE strategically interleaves standard CNN and Transformer blocks with novel KANConv and KAT blocks, enabling the model to form a comprehensive feature representation. To optimize feature processing, we integrate several critical components into the HDBE. First, a Cross-Branch Channel Interaction (CCI) module is embedded to facilitate efficient interaction of channel features between the parallel pathways. Second, an attention-based Spatial Feature Enhancement (SFE) module is employed to enhance spatial features and fuse the outputs from both branches. Building upon the SFE module, an advanced Spatial Feature Enhancement with Geometrically Adaptive Fusion (SFE-GAF) module is subsequently developed. In the SFE-GAF module, adaptive sampling is utilized to focus on true vessel morphology precisely. The adaptive process strengthens salient vascular features while significantly reducing background noise and computational overhead. Extensive experiments on the DRIVE, STARE, and CHASE_DB1 datasets validate that DB-KAUNet achieves leading segmentation performance and demonstrates exceptional robustness.

Refining Heuristic Predictors of Fractional Chern Insulators using Machine Learning

Authors: Oriol Mayné i Comas, André Grossi Fonseca, Sachin Vaidya, Marin Soljačić

Abstract: We develop an interpretable, data-driven framework to quantify how single-particle band geometry governs the stability of fractional Chern insulators (FCIs). Using large-scale exact diagonalization, we evaluate an FCI metric that yields a continuous spectral measure of FCI stability across parameter space. We then train Kolmogorov-Arnold networks (KANs) – a recently developed interpretable neural architecture – to regress this metric from two band-geometric descriptors: the trace violation $T$ and the Berry curvature fluctuations $σ_B$. Applied to spinless fermions at filling $ν=1/3$ in models on the checkerboard and kagome lattices, our approach yields compact analytical formulas that predict FCI stability with over $>80 \%$ accuracy in both regression and classification tasks, and remain reliable even in data-scarce regimes. The learned relations reveal model-dependent trends, clarifying the limits of Landau-level-mimicking heuristics. Our framework provides a general method for extracting simple, phenomenological “laws” that connect many-body phase stability to chosen physical descriptors, enabling rapid hypothesis formation and targeted design of quantum phases.

Assessing the performance of correlation-based multi-fidelity neural emulators

Authors: Cristian J. Villatoro, Gianluca Geraci, Daniele E. Schiavazzi

Abstract: Outer loop tasks such as optimization, uncertainty quantification or inference can easily become intractable when the underlying high-fidelity model is computationally expensive. Similarly, data-driven architectures typically require large datasets to perform predictive tasks with sufficient accuracy. A possible approach to mitigate these challenges is the development of multi-fidelity emulators, leveraging potentially biased, inexpensive low-fidelity information while correcting and refining predictions using scarce, accurate high-fidelity data. This study investigates the performance of multi-fidelity neural emulators, neural networks designed to learn the input-to-output mapping by integrating limited high-fidelity data with abundant low-fidelity model solutions. We investigate the performance of such emulators for low and high-dimensional functions, with oscillatory character, in the presence of discontinuities, for collections of models with equal and dissimilar parametrization, and for a possibly large number of potentially corrupted low-fidelity sources. In doing so, we consider a large number of architectural, hyperparameter, and dataset configurations including networks with a different amount of spectral bias (Multi-Layered Perceptron, Siren and Kolmogorov Arnold Network), various mechanisms for coordinate encoding, exact or learnable low-fidelity information, and for varying training dataset size. We further analyze the added value of the multi-fidelity approach by conducting equivalent single-fidelity tests for each case, quantifying the performance gains achieved through fusing multiple sources of information.

QKAN-LSTM: Quantum-inspired Kolmogorov-Arnold Long Short-term Memory

Authors: Yu-Chao Hsu, Jiun-Cheng Jiang, Chun-Hua Lin, Kuo-Chung Peng, Nan-Yow Chen, Samuel Yen-Chi Chen, En-Jui Kuo, Hsi-Sheng Goan

Abstract: Long short-term memory (LSTM) models are a particular type of recurrent neural networks (RNNs) that are central to sequential modeling tasks in domains such as urban telecommunication forecasting, where temporal correlations and nonlinear dependencies dominate. However, conventional LSTMs suffer from high parameter redundancy and limited nonlinear expressivity. In this work, we propose the Quantum-inspired Kolmogorov-Arnold Long Short-Term Memory (QKAN-LSTM), which integrates Data Re-Uploading Activation (DARUAN) modules into the gating structure of LSTMs. Each DARUAN acts as a quantum variational activation function (QVAF), enhancing frequency adaptability and enabling an exponentially enriched spectral representation without multi-qubit entanglement. The resulting architecture preserves quantum-level expressivity while remaining fully executable on classical hardware. Empirical evaluations on three datasets, Damped Simple Harmonic Motion, Bessel Function, and Urban Telecommunication, demonstrate that QKAN-LSTM achieves superior predictive accuracy and generalization with a 79% reduction in trainable parameters compared to classical LSTMs. We extend the framework to the Jiang-Huang-Chen-Goan Network (JHCG Net), which generalizes KAN to encoder-decoder structures, and then further use QKAN to realize the latent KAN, thereby creating a Hybrid QKAN (HQKAN) for hierarchical representation learning. The proposed HQKAN-LSTM thus provides a scalable and interpretable pathway toward quantum-inspired sequential modeling in real-world data environments.

Uncertainty Quantification for Scientific Machine Learning using Sparse Variational Gaussian Process Kolmogorov-Arnold Networks (SVGP KAN)

Author: Y. Sungtaek Ju

Abstract: Kolmogorov-Arnold Networks have emerged as interpretable alternatives to traditional multi-layer perceptrons. However, standard implementations lack principled uncertainty quantification capabilities essential for many scientific applications. We present a framework integrating sparse variational Gaussian process inference with the Kolmogorov-Arnold topology, enabling scalable Bayesian inference with computational complexity quasi-linear in sample size. Through analytic moment matching, we propagate uncertainty through deep additive structures while maintaining interpretability. We use three example studies to demonstrate the framework’s ability to distinguish aleatoric from epistemic uncertainty: calibration of heteroscedastic measurement noise in fluid flow reconstruction, quantification of prediction confidence degradation in multi-step forecasting of advection-diffusion dynamics, and out-of-distribution detection in convolutional autoencoders. These results suggest Sparse Variational Gaussian Process Kolmogorov-Arnold Networks (SVGP KANs) is a promising architecture for uncertainty-aware learning in scientific machine learning.

The T12 System for AudioMOS Challenge 2025: Audio Aesthetics Score Prediction System Using KAN- and VERSA-based Models

Authors: Katsuhiko Yamamoto, Koichi Miyazaki, Shogo Seki

Abstract: We propose an audio aesthetics score (AES) prediction system by CyberAgent (AESCA) for AudioMOS Challenge 2025 (AMC25) Track 2. The AESCA comprises a Kolmogorov–Arnold Network (KAN)-based audiobox aesthetics and a predictor from the metric scores using the VERSA toolkit. In the KAN-based predictor, we replaced each multi-layer perceptron layer in the baseline model with a group-rational KAN and trained the model with labeled and pseudo-labeled audio samples. The VERSA-based predictor was designed as a regression model using extreme gradient boosting, incorporating outputs from existing metrics. Both the KAN- and VERSA-based models predicted the AES, including the four evaluation axes. The final AES values were calculated using an ensemble model that combined four KAN-based models and a VERSA-based model. Our proposed T12 system yielded the best correlations among the submitted systems, in three axes at the utterance level, two axes at the system level, and the overall average. We also released the inference model of the proposed KAN-based predictor (KAN #1-#4).

KANFormer for Predicting Fill Probabilities via Survival Analysis in Limit Order Books

Authors: Jinfeng Zhong, Emmanuel Bacry, Agathe Guilloux, Jean-François Muzy

Abstract: This paper introduces KANFormer, a novel deep-learning-based model for predicting the time-to-fill of limit orders by leveraging both market- and agent-level information. KANFormer combines a Dilated Causal Convolutional network with a Transformer encoder, enhanced by Kolmogorov-Arnold Networks (KANs), which improve nonlinear approximation. Unlike existing models that rely solely on a series of snapshots of the limit order book, KANFormer integrates the actions of agents related to LOB dynamics and the position of the order in the queue to more effectively capture patterns related to execution likelihood. We evaluate the model using CAC 40 index futures data with labeled orders. The results show that KANFormer outperforms existing works in both calibration (Right-Censored Log-Likelihood, Integrated Brier Score) and discrimination (C-index, time-dependent AUC). We further analyze feature importance over time using SHAP (SHapley Additive exPlanations). Our results highlight the benefits of combining rich market signals with expressive neural architectures to achieve accurate and interpretabl predictions of fill probabilities.

Entanglement Witness Derived By Using Kolmogorov-Arnold Networks

Authors: Fatemeh Lajevardi, Azam Mani, Ali Fahim

Abstract: We utilize Kolmogorov-Arnold Networks to design an interpretable model capable of detecting quantum entanglement within a set of nine-parameter two-qubit states. This network serves as an entanglement witness, achieving an accuracy of $94\%$ in distinguishing entangled states. Additionally, by analyzing the output functions of the KAN models, we explore the significance of each parameter (feature) in identifying the presence of entanglement. This analysis enables us to rank the features and eliminate the less significant ones, leading to the development of new entanglement witness functions that rely on fewer number of features, and hence do not require complete state tomography for their evaluation.

KAN-Dreamer: Benchmarking Kolmogorov-Arnold Networks as Function Approximators in World Models

Authors: Chenwei Shi, Xueyu Luan

Abstract: DreamerV3 is a state-of-the-art online model-based reinforcement learning (MBRL) algorithm known for remarkable sample efficiency. Concurrently, Kolmogorov-Arnold Networks (KANs) have emerged as a promising alternative to Multi-Layer Perceptrons (MLPs), offering superior parameter efficiency and interpretability. To mitigate KANs’ computational overhead, variants like FastKAN leverage Radial Basis Functions (RBFs) to accelerate inference. In this work, we investigate integrating KAN architectures into the DreamerV3 framework. We introduce KAN-Dreamer, replacing specific MLP and convolutional components of DreamerV3 with KAN and FastKAN layers. To ensure efficiency within the JAX-based World Model, we implement a tailored, fully vectorized version with simplified grid management. We structure our investigation into three subsystems: Visual Perception, Latent Prediction, and Behavior Learning. Empirical evaluations on the DeepMind Control Suite (walker_walk) analyze sample efficiency, training time, and asymptotic performance. Experimental results demonstrate that utilizing our adapted FastKAN as a drop-in replacement for the Reward and Continue predictors yields performance on par with the original MLP-based architecture, maintaining parity in both sample efficiency and training speed. This report serves as a preliminary study for future developments in KAN-based world models.

Trapped Fermions Through Kolmogorov-Arnold Wavefunctions

Authors: Paulo F. Bedaque, Jacob Cigliano, Hersh Kumar, Srijit Paul, Suryansh Rajawat

Abstract: We investigate a variational Monte Carlo framework for trapped one-dimensional mixture of spin-$\frac{1}{2}$ fermions using Kolmogorov-Arnold networks (KANs) to construct universal neural-network wavefunction ansätze. The method can, in principle, achieve arbitrary accuracy, limited only by the Monte Carlo sampling and was checked against exact results at sub-percent precision. For attractive interactions, it captures pairing effects, and in the impurity case it agrees with known results. We present a method of systematic transfer learning in the number of network parameters, allowing for efficient training for a target precision. We vastly increase the efficiency of the method by incorporating the short-distance behavior of the wavefunction into the ansätz without biasing the method.

Softly Symbolifying Kolmogorov-Arnold Networks

Authors: James Bagrow, Josh Bongard

Abstract: Kolmogorov-Arnold Networks (KANs) offer a promising path toward interpretable machine learning: their learnable activations can be studied individually, while collectively fitting complex data accurately. In practice, however, trained activations often lack symbolic fidelity, learning pathological decompositions with no meaningful correspondence to interpretable forms. We propose Softly Symbolified Kolmogorov-Arnold Networks (S2KAN), which integrate symbolic primitives directly into training. Each activation draws from a dictionary of symbolic and dense terms, with learnable gates that sparsify the representation. Crucially, this sparsification is differentiable, enabling end-to-end optimization, and is guided by a principled Minimum Description Length objective. When symbolic terms suffice, S2KAN discovers interpretable forms; when they do not, it gracefully degrades to dense splines. We demonstrate competitive or superior accuracy with substantially smaller models across symbolic benchmarks, dynamical systems forecasting, and real-world prediction tasks, and observe evidence of emergent self-sparsification even without regularization pressure.

GS-KAN: Parameter-Efficient Kolmogorov-Arnold Networks via Sprecher-Type Shared Basis Functions

Author: Oscar Eliasson

Abstract: The Kolmogorov-Arnold representation theorem offers a theoretical alternative to Multi-Layer Perceptrons (MLPs) by placing learnable univariate functions on edges rather than nodes. While recent implementations such as Kolmogorov-Arnold Networks (KANs) demonstrate high approximation capabilities, they suffer from significant parameter inefficiency due to the requirement of maintaining unique parameterizations for every network edge. In this work, we propose GS-KAN (Generalized Sprecher-KAN), a lightweight architecture inspired by David Sprecher’s refinement of the superposition theorem. GS-KAN constructs unique edge functions by applying learnable linear transformations to a single learnable, shared parent function per layer. We evaluate GS-KAN against existing KAN architectures and MLPs across synthetic function approximation, tabular data regression and image classification tasks. Our results demonstrate that GS-KAN outperforms both MLPs and standard KAN baselines on continuous function approximation tasks while maintaining superior parameter efficiency. Additionally, GS-KAN achieves competitive performance with existing KAN architectures on tabular regression and outperforms MLPs on high-dimensional classification tasks. Crucially, the proposed architecture enables the deployment of KAN-based architectures in high-dimensional regimes under strict parameter constraints, a setting where standard implementations are typically infeasible due to parameter explosion. The source code is available at https://github.com/rambamn48/gs-impl.

Generative Adversarial Variational Quantum Kolmogorov-Arnold Network

Author: Hikaru Wakaura

Abstract: Kolmogorov Arnold Networks is a novel multilayer neuromorphic network that can exhibit higher accuracy than a neural network. It can learn and predict more accurately than neural networks with a smaller number of parameters, and many research groups worldwide have adopted it. As a result, many types of applications have been proposed. This network can be used as a generator solely or with a Generative Adversarial Network; however, KAN has a slower speed of learning than neural networks for the number of parameters. Hence,it has not been researched as a generator. Therefore, we propose a novel Generative Adversarial Network called Generative Adversarial Variational Quantum KAN that uses Variational Quantum KAN as a generator. This method enables efficient learning with significantly fewer parameters by leveraging the computational advantages of quantum circuits and their output distributions. We performed the training and generation task on MNIST and CIFAR10, and revealed that our method can achieve higher accuracy than neural networks and Quantum Generative Adversarial Network with less data.

Solving the Cosmological Vlasov-Poisson Equations with Physics-Informed Kolmogorov-Arnold Networks

Authors: Nicolas Cerardi, Emma Tolley, Ashutosh Mishra

Abstract: Cold dark matter (CDM) evolves as a collisionless fluid under the Vlasov-Poisson equations, but N-body simulations approximate this evolution by discretising the distribution function into particles, introducing discreteness effects at small scales. We present a physics-informed neural network approach that evolves CDM fields without any use of N-body data or methods, using a Kolmogorov-Arnold network (KAN) to model the continuous displacement field for one-dimensional halo collapse. Physical constraints derived from the Vlasov-Poisson equations are embedded directly into the loss function, enabling accurate evolution beyond the first shell crossing. The trained model achieves sub-percent errors on the residuals even after seven shell crossings and matches N-body results while providing a resolution-free representation of the displacement field. In addition, displacement errors do not grow over time, a very interesting feature with respect to N-body methods. It can also reconstruct initial conditions through backward evolution when sufficient final-state information is available. Although current runtimes exceed those of N-body methods, this framework offers a new route to high-fidelity CDM evolution without particle discretisation, with prospects for extension to higher dimensions.

HWF-PIKAN: A Multi-Resolution Hybrid Wavelet-Fourier Physics-Informed Kolmogorov-Arnold Network for solving Collisionless Boltzmann Equation

Authors: Mohammad E. Heravifard, Kazem Hejranfar

Abstract: Physics-Informed Neural Networks (PINNs) and more recently Physics-Informed Kolmogorov-Arnold Networks (PIKANs) have emerged as promising approaches for solving partial differential equations (PDEs) without reliance on extensive labeled data. In this work, we propose a novel multi-resolution Hybrid Wavelet-Fourier-Enhanced Physics-Informed Kolmogorov-Arnold Network (HWF-PIKAN) for solving advection problems based on collisionless Boltzmann equation (CBE) with both continuous and discontinuous initial conditions. To validate the effectiveness of the proposed model, we conduct systematic benchmarks on classical advection equations in one and two dimensions. These tests demonstrate the model’s ability to accurately capture smooth and abrupt features. We then extend the application of HWF-PIKAN to the high-dimensional phase-space setting by solving the CBE in a continuous-velocity manner. This leverages the Hamiltonian concept of phase-space dynamics to model the statistical behavior of particles in a collisionless system, where advection governs the evolution of a probability distribution function or number density. Comparative analysis against Vanilla PINN, Vanilla PIKAN, as well as Fourier-enhanced and Wavelet-enhanced PIKAN variants, shows that the proposed hybrid model significantly improves solution accuracy and convergence speed. This study highlights the power of multi-resolution spectral feature embeddings in advancing physics-informed deep learning frameworks for complex kinetic equations in both space-time and phase-space.

Physics-informed neural networks to solve inverse problems in unbounded domains

Authors: Gregorio Pérez-Bernal, Oscar Rincón-Cardeño, Silvana Montoya-Noguera, Nicolás Guarín-Zapata

Abstract: Inverse problems are extensively studied in applied mathematics, with applications ranging from acoustic tomography for medical diagnosis to geophysical exploration. Physics informed neural networks (PINNs) have emerged as a powerful tool for solving such problems, while Physics informed Kolmogorov Arnold networks (PIKANs) represent a recent benchmark that, in certain problems, promises greater interpretability and accuracy compared to PINNs, due to their nature, being constructed as a composition of polynomials. In this work, we develop a methodology for addressing inverse problems in infinite and semi infinite domains. We introduce a novel sampling strategy for the network’s training points, using the negative exponential and normal distributions, alongside a dual network architecture that is trained to learn the solution and parameters of an equation with the same loss function. This design enables the solution of inverse problems without explicitly imposing boundary conditions, as long as the solutions tend to stabilize when leaving the domain of interest. The proposed architecture is implemented using both PINNs and PIKANs, and their performance is compared in terms of accuracy with respect to a known solution as well as computational time and response to a noisy environment. Our results demonstrate that, in this setting, PINNs provide a more accurate and computationally efficient solution, solving the inverse problem 1,000 times faster and in the same order of magnitude, yet with a lower relative error than PIKANs.

Optimized Architectures for Kolmogorov-Arnold Networks

Authors: James Bagrow, Josh Bongard

Abstract: Efforts to improve Kolmogorov–Arnold networks (KANs) with architectural enhancements have been stymied by the complexity those enhancements bring, undermining the interpretability that makes KANs attractive in the first place. Here we study overprovisioned architectures combined with sparsification, deep supervision, and depth selection, to learn compact, interpretable KANs without sacrificing accuracy. Crucially, we focus on differentiable mechanisms under a principled minimum description length objective, jointly optimizing activations, structure, and depth end-to-end. Experiments across function approximation benchmarks, dynamical systems forecasting, and real-world prediction tasks demonstrate that sparsification alone is insufficient, but the combination with depth selection achieves competitive or superior accuracy while discovering substantially smaller models. The result is a principled path toward models that are both more expressive and more interpretable, addressing a key tension in scientific machine learning.

KANELÉ: Kolmogorov-Arnold Networks for Efficient LUT-based Evaluation

Authors: Duc Hoang, Aarush Gupta, Philip Harris

Abstract: Low-latency, resource-efficient neural network inference on FPGAs is essential for applications demanding real-time capability and low power. Lookup table (LUT)-based neural networks are a common solution, combining strong representational power with efficient FPGA implementation. In this work, we introduce KANELÉ, a framework that exploits the unique properties of Kolmogorov-Arnold Networks (KANs) for FPGA deployment. Unlike traditional multilayer perceptrons (MLPs), KANs employ learnable one-dimensional splines with fixed domains as edge activations, a structure naturally suited to discretization and efficient LUT mapping. We present the first systematic design flow for implementing KANs on FPGAs, co-optimizing training with quantization and pruning to enable compact, high-throughput, and low-latency KAN architectures. Our results demonstrate up to a 2700x speedup and orders of magnitude resource savings compared to prior KAN-on-FPGA approaches. Moreover, KANELÉ matches or surpasses other LUT-based architectures on widely used benchmarks, particularly for tasks involving symbolic or physical formulas, while balancing resource usage across FPGA hardware. Finally, we showcase the versatility of the framework by extending it to real-time, power-efficient control systems.

Learning continuous state of charge dependent thermal decomposition kinetics for Li-ion cathodes using Kolmogorov-Arnold Chemical Reaction Neural Networks (KA-CRNNs)

Authors: Benjamin C. Koenig, Sili Deng

Abstract: Thermal runaway in lithium-ion batteries is strongly influenced by the state of charge (SOC). Existing predictive models typically infer scalar kinetic parameters at a full SOC or a few discrete SOC levels, preventing them from capturing the continuous SOC dependence that governs exothermic behavior during abuse conditions. To address this, we apply the Kolmogorov-Arnold Chemical Reaction Neural Network (KA-CRNN) framework to learn continuous and realistic SOC-dependent exothermic cathode-electrolyte interactions. We apply a physics-encoded KA-CRNN to learn SOC-dependent kinetic parameters for cathode-electrolyte decomposition directly from differential scanning calorimetry (DSC) data. A mechanistically informed reaction pathway is embedded into the network architecture, enabling the activation energies, pre-exponential factors, enthalpies, and related parameters to be represented as continuous and fully interpretable functions of the SOC. The framework is demonstrated for NCA, NM, and NMA cathodes, yielding models that reproduce DSC heat-release features across all SOCs and provide interpretable insight into SOC-dependent oxygen-release and phase-transformation mechanisms. This approach establishes a foundation for extending kinetic parameter dependencies to additional environmental and electrochemical variables, supporting more accurate and interpretable thermal runaway prediction and monitoring.

SHARe-KAN: Post-Training Vector Quantization for Cache-Resident KAN Inference

Author: Jeff Smith

Abstract: Pre-trained Vision Kolmogorov-Arnold Networks (KANs) store a dense B-spline grid on every edge, inflating prediction-head parameter counts by more than 140X relative to a comparable MLP and pushing inference into a memory-bound regime on edge accelerators. Standard magnitude pruning fails on these pre-trained models: zero-shot sparsity collapses accuracy, and restoring it requires an iterative fine-tuning loop that is impractical in deployment settings. We present SHARe-KAN, a post-training compiler that compresses spline coefficients via a Gain-Shape-Bias decomposition with a layer-shared codebook, paired with LUTHAM, an ExecuTorch runtime that maps the codebook into on-chip L2. On PASCAL VOC detection with a ResNet-50 backbone, SHARe-KAN Int8 reaches 9.3X storage compression over the Dense KAN baseline (6.32 MB vs. 58.67 MB prediction head) at a 2.0 point in-domain accuracy cost (80.22% vs. 82.22% mAP), with no retraining. Zero-shot transfer to COCO retains 88.9% of the Dense KAN mAP; most of this gap comes from the VQ clustering step itself, and further quantization from FP32 to Int8 costs only 1.3 retention points. The value of the approach compounds at scale: at 50 task heads, Dense KAN prediction-head storage reaches 2.9 GB while SHARe-KAN Int8 requires 211 MB, a 13.9X reduction that brings multi-expert KAN deployment within the memory budgets of contemporary edge silicon.

KAN-Matrix: Visualizing Nonlinear Pairwise and Multivariate Contributions for Physical Insight

Authors: Luis A. De la Fuente, Hernan A. Moreno, Laura V. Alvarez, Hoshin V. Gupta

Abstract: Interpreting complex datasets remains a major challenge for scientists, particularly due to high dimensionality and collinearity among variables. We introduce a novel application of Kolmogorov-Arnold Networks (KANs) to enhance interpretability and parsimony beyond what traditional correlation analyses offer. We present two interpretable, color-coded visualization tools: the Pairwise KAN Matrix (PKAN) and the Multivariate KAN Contribution Matrix (MKAN). PKAN characterizes nonlinear associations between pairs of variables, while MKAN serves as a nonlinear feature-ranking tool that quantifies the relative contributions of inputs in predicting a target variable. These tools support pre-processing (e.g., feature selection, redundancy analysis) and post-processing (e.g., model explanation, physical insights) in model development workflows. Through experimental comparisons, we demonstrate that PKAN and MKAN yield more robust and informative results than Pearson Correlation and Mutual Information. By capturing the strength and functional forms of relationships, these matrices facilitate the discovery of hidden physical patterns and promote domain-informed model development.

MINPO: Memory-Informed Neural Pseudo-Operator to Resolve Nonlocal Spatiotemporal Dynamics

Authors: Farinaz Mostajeran, Aruzhan Tleubek, Salah A Faroughi

Abstract: Many physical systems exhibit nonlocal spatiotemporal behaviors described by integro-differential equations (IDEs). Classical methods for solving IDEs require repeatedly evaluating convolution integrals, whose cost increases quickly with kernel complexity and dimensionality. Existing neural solvers can accelerate selected instances of these computations, yet they do not generalize across diverse nonlocal structures. In this work, we introduce the Memory-Informed Neural Pseudo-Operator (MINPO), a unified framework for modeling nonlocal dynamics arising from long-range spatial interactions and/or long-term temporal memory. MINPO, employing either Kolmogorov-Arnold Networks (KANs) or multilayer perceptron networks (MLPs) as encoders, learns the nonlocal operator and its inverse directly through neural representations, and then explicitly reconstruct the unknown solution fields. The learning is guarded by a lightweight nonlocal consistency loss term to enforce coherence between the learned operator and reconstructed solution. The MINPO formulation allows to naturally capture and efficiently resolve nonlocal spatiotemporal dependencies governed by a wide spectrum of IDEs and their subsets, including fractional PDEs. We evaluate the efficacy of MINPO in comparison with classical techniques and state-of-the-art neural-based strategies based on MLPs, such as A-PINN and fPINN, along with their newly-developed KAN variants, A-PIKAN and fPIKAN, designed to facilitate a fair comparison. Our study offers compelling evidence of the accuracy of MINPO and demonstrates its robustness in handling (i) diverse kernel types, (ii) different kernel dimensionalities, and (iii) the substantial computational demands arising from repeated evaluations of kernel integrals. MINPO, thus, generalizes beyond problem-specific formulations, providing a unified framework for systems governed by nonlocal operators.

Concurrent training methods for Kolmogorov-Arnold networks: Disjoint datasets and FPGA implementation

Authors: Andrew Polar, Michael Poluektov

Abstract: The present paper introduces concurrency-driven enhancements to the training algorithm for the Kolmogorov-Arnold networks (KANs) that is based on the Newton-Kaczmarz (NK) method. Prior research shows that KANs trained using the NK-based approach significantly overtake classical neural networks based on multilayer perceptrons (MLPs) in terms of accuracy and training time. Although some parts of the algorithm, such as the evaluation of the basis functions, can be parallelised, the fundamental limitation lies in the sequential computation of the updates - each update depends on the results of the previous step, obstructing parallelisation. However, substantial acceleration is achievable. Three complementary strategies are proposed in the present paper: (i) a pre-training procedure tailored to the NK updates’ structure, (ii) training on disjoint subsets of data, followed by models’ merging, not in the context of federated learning, but as a mechanism for accelerating the convergence, and (iii) a parallelisation technique suitable for execution on field-programmable gate arrays (FPGAs), which is implemented and tested directly on the device. With these novel techniques, computational experiments show that KANs can be trained more than 40 times faster than neural networks, when training is done to the same accuracy on CPUs. All presented experimental results are fully reproducible, with the complete source codes available online.

Sprecher Networks: A Parameter-Efficient Kolmogorov-Arnold Architecture

Authors: Christian Hägg, Kathlén Kohn, Giovanni Luca Marchetti, Boris Shapiro

Abstract: We introduce Sprecher Networks (SNs), a family of trainable architectures derived from David Sprecher’s 1965 constructive form of the Kolmogorov-Arnold representation. Each SN block implements a “sum of shifted univariate functions” using only two shared learnable splines per block, a monotone inner spline $φ$ and a general outer spline $Φ$, together with a learnable shift parameter $η$ and a mixing vector $λ$ shared across all output dimensions. Stacking these blocks yields deep, compositional models; for vector-valued outputs we append an additional non-summed output block. We also propose an optional lateral mixing operator enabling intra-block communication between output channels with only $O(d_{\mathrm{out}})$ additional parameters. Owing to the vector (not matrix) mixing weights and spline sharing, SNs scale linearly in width, approximately $O(\sum_{\ell}(d_{\ell-1}+d_{\ell}+G))$ parameters for $G$ spline knots, versus $O(\sum_{\ell} d_{\ell-1}d_{\ell})$ for dense MLPs and $O(G\sum_{\ell} d_{\ell-1}d_{\ell})$ for edge-spline KANs. This linear width-scaling is particularly attractive for extremely wide, shallow models, where low depth can translate into low inference latency. Finally, we describe a sequential forward implementation that avoids materializing the $d_{\mathrm{in}}\times d_{\mathrm{out}}$ shifted-input tensor, reducing peak forward-intermediate memory from quadratic to linear in layer width, relevant for memory-constrained settings such as on-device/edge inference; we demonstrate deployability via fixed-point real-time digit classification on resource-constrained embedded device with only 4 MB RAM. We provide empirical demonstrations on supervised regression, Fashion-MNIST classification (including stable training at 25 hidden layers with residual connections and normalization), and a Poisson PINN, with controlled comparisons to MLP and KAN baselines.

Kolmogorov-Arnold graph neural networks for chemically informed prediction tasks on inorganic nanomaterials

Authors: Nikita Volzhin, Soowhan Yoon

Abstract: The recent development of Kolmogorov-Arnold Networks (KANs) has found its application in the field of Graph Neural Networks (GNNs) particularly in molecular data modeling and potential drug discovery. Kolmogorov-Arnold Graph Neural Networks (KAGNNs) expand on the existing set of GNN models with KAN-based counterparts. KAGNNs have been demonstrably successful in surpassing the accuracy of MultiLayer Perceptron (MLP)-based GNNs in the task of molecular property prediction. These models were widely tested on the graph datasets consisting of organic molecules. In this study, we explore the application of KAGNNs towards inorganic nanomaterials. In 2024, a large scale inorganic nanomaterials dataset was published under the title CHILI (Chemically-Informed Large-scale Inorganic Nanomaterials Dataset), and various MLP-based GNNs have been tested on this dataset. We adapt and test our own KAGNNs appropriate for eight defined tasks. Our experiments reveal that, KAGNNs frequently surpass the performance of their counterpart GNNs. Most notably, on crystal system and space group classification tasks in CHILI-3K, KAGNNs achieve the new state-of-the-art results of 99.5 percent and 96.6 percent accuracy, respectively, compared to the previous 65.7 and 73.3 percent each.

Deep Legendre Transform

Authors: Aleksey Minabutdinov, Patrick Cheridito

Abstract: We introduce a novel deep learning algorithm for computing convex conjugates of differentiable convex functions, a fundamental operation in convex analysis with various applications in different fields such as optimization, control theory, physics and economics. While traditional numerical methods suffer from the curse of dimensionality and become computationally intractable in high dimensions, more recent neural network–based approaches scale better, but have mostly been studied with the aim of solving optimal transport problems and require the solution of complicated optimization or max–min problems. Using an implicit Fenchel formulation of convex conjugation, our approach facilitates an efficient gradient–based framework for the minimization of approximation errors and, as a byproduct, also provides a posteriori estimates of the approximation accuracy. Numerical experiments demonstrate our method’s ability to deliver accurate results across different high-dimensional examples. Moreover, by employing symbolic regression with Kolmogorov–Arnold networks, it is able to obtain the exact convex conjugates of specific convex functions.

DecoKAN: Interpretable Decomposition for Forecasting Cryptocurrency Market Dynamics

Authors: Yuan Gao, Zhenguo Dong, Xuelong Wang, Zhiqiang Wang, Yong Zhang, Shaofan Wang

Abstract: Accurate and interpretable forecasting of multivariate time series is crucial for understanding the complex dynamics of cryptocurrency markets in digital asset systems. Advanced deep learning methodologies, particularly Transformer-based and MLP-based architectures, have achieved competitive predictive performance in cryptocurrency forecasting tasks. However, cryptocurrency data is inherently composed of long-term socio-economic trends and local high-frequency speculative oscillations. Existing deep learning-based ‘black-box’ models fail to effectively decouple these composite dynamics or provide the interpretability needed for trustworthy financial decision-making. To overcome these limitations, we propose DecoKAN, an interpretable forecasting framework that integrates multi-level Discrete Wavelet Transform (DWT) for decoupling and hierarchical signal decomposition with Kolmogorov-Arnold Network (KAN) mixers for transparent and interpretable nonlinear modeling. The DWT component decomposes complex cryptocurrency time series into distinct frequency components, enabling frequency-specific analysis, while KAN mixers provide intrinsically interpretable spline-based mappings within each decomposed subseries. Furthermore, interpretability is enhanced through a symbolic analysis pipeline involving sparsification, pruning, and symbolization, which produces concise analytical expressions offering symbolic representations of the learned patterns. Extensive experiments demonstrate that DecoKAN achieves the lowest average Mean Squared Error on all tested real-world cryptocurrency datasets (BTC, ETH, XMR), consistently outperforming a comprehensive suite of competitive state-of-the-art baselines. These results validate DecoKAN’s potential to bridge the gap between predictive accuracy and model transparency, advancing trustworthy decision support within complex cryptocurrency markets.

From GNNs to Symbolic Surrogates via Kolmogorov-Arnold Networks for Delay Prediction

Authors: Sami Marouani, Kamal Singh, Baptiste Jeudy, Amaury Habrard

Abstract: Accurate prediction of flow delay is essential for optimizing and managing modern communication networks. We investigate three levels of modeling for this task. First, we implement a heterogeneous GNN with attention-based message passing, establishing a strong neural baseline. Second, we propose FlowKANet in which Kolmogorov-Arnold Networks replace standard MLP layers, reducing trainable parameters while maintaining competitive predictive performance. FlowKANet integrates KAMP-Attn (Kolmogorov-Arnold Message Passing with Attention), embedding KAN operators directly into message-passing and attention computation. Finally, we distill the model into symbolic surrogate models using block-wise regression, producing closed-form equations that eliminate trainable weights while preserving graph-structured dependencies. The results show that KAN layers provide a favorable trade-off between efficiency and accuracy and that symbolic surrogates emphasize the potential for lightweight deployment and enhanced transparency.

Lyapunov-Based Kolmogorov-Arnold Network (KAN) Adaptive Control

Authors: Xuehui Shen, Wenqian Xue, Yixuan Wang, Warren E. Dixon

Abstract: Recent advancements in Lyapunov-based Deep Neural Networks (Lb-DNNs) have demonstrated improved performance over shallow NNs and traditional adaptive control for nonlinear systems with uncertain dynamics. Existing Lb-DNNs rely on multi-layer perceptrons (MLPs), which lack interpretable insights. As a first step towards embedding interpretable insights in the control architecture, this paper develops the first Lyapunov-based Kolmogorov-Arnold Networks (Lb-KAN) adaptive control method for uncertain nonlinear systems. Unlike MLPs with deep-layer matrix multiplications, KANs provide interpretable insights by direct functional decomposition. In this framework, KANs are employed to approximate uncertain dynamics and embedded into the control law, enabling visualizable functional decomposition. The analytical update laws are constructed from a Lyapunov-based analysis for real-time learning without prior data in a KAN architecture. The analysis uses the distinct KAN approximation theorem to formally bound the reconstruction error and its effect on the performance. The update law is derived by incorporating the KAN’s learnable parameters into a Jacobian matrix, enabling stable, analytical, real-time adaptation and ensuring asymptotic convergence of tracking errors. Moreover, the Lb-KAN provides a foundation for interpretability characteristics by achieving visualizable functional decomposition. Simulation results demonstrate that the Lb-KAN controller reduces the function approximation error by 20.2% and 18.0% over the baseline Lb-LSTM and Lb-DNN methods, respectively.

Synergizing Kolmogorov-Arnold Networks with Dynamic Adaptive Weighting for High-Frequency and Multi-Scale PDE Solutions

Authors: Guokan Chen, Yao Xiao, Bin Fan, Meixin Xionga, Zhicheng Lin, Yuanying Liu

Abstract: PINNs enhance scientific computing by incorporating physical laws into neural network structures, leading to significant advancements in scientific computing. However, PINNs struggle with multi-scale and high-frequency problems due to pathological gradient flow and spectral bias, which severely limit their predictive power. By combining an enhanced network architecture with a dynamically adaptive weighting mechanism featuring upper-bound constraints, we propose the Dynamic Balancing Adaptive Weighting Physics-Informed Kolmogorov-Arnold Network (DBAW-PIKAN). The proposed method effectively mitigates gradient-related failure modes and overcomes bottlenecks in function representation. Compared to baseline models, the proposed method accelerates the convergence process and improves solution accuracy by at least an order of magnitude without introducing additional computational complexity. Numerical results on the Klein-Gordon, Burgers, and Helmholtz equations demonstrate that DBAW-PIKAN achieves superior accuracy and generalization performance.

Integrating Wide and Deep Neural Networks with Squeeze-and-Excitation Blocks for Multi-Target Property Prediction in Additively Manufactured Fiber Reinforced Composites

Authors: Behzad Parvaresh, Rahmat K. Adesunkanmi, Adel Alaeddini

Abstract: Continuous fiber-reinforced composite manufactured by additive manufacturing (CFRC-AM) offers opportunities for printing lightweight materials with high specific strength. However, their performance is sensitive to the interaction of process and material parameters, making exhaustive experimental testing impractical. In this study, we introduce a data-efficient, multi-input, multi-target learning approach that integrates Latin Hypercube Sampling (LHS)-guided experimentation with a squeeze-and-excitation wide and deep neural network (SE-WDNN) to jointly predict multiple mechanical and manufacturing properties of CFRC-AMs based on different manufacturing parameters. We printed and tested 155 specimens selected from a design space of 4,320 combinations using a Markforged Mark Two 3D printer. The processed data formed the input-output set for our proposed model. We compared the results with those from commonly used machine learning models, including feedforward neural networks, Kolmogorov-Arnold networks, XGBoost, CatBoost, and random forests. Our model achieved the lowest overall test error (MAPE = 12.33%) and showed statistically significant improvements over the baseline wide and deep neural network for several target variables (paired t-tests, p <= 0.05). SHapley Additive exPlanations (SHAP) analysis revealed that reinforcement strategy was the major influence on mechanical performance. Overall, this study demonstrates that the integration of LHS and SE-WDNN enables interpretable and sample-efficient multi-target predictions, guiding parameter selection in CFRC-AM with a balance between mechanical behavior and manufacturing metrics.

Uncertainty-Aware Flow Field Reconstruction Using SVGP Kolmogorov-Arnold Networks

Author: Y. Sungtaek Ju

Abstract: Reconstructing time-resolved flow fields from temporally sparse velocimetry measurements is critical for characterizing many complex thermal-fluid systems. We introduce a machine learning framework for uncertainty-aware flow reconstruction using sparse variational Gaussian processes in the Kolmogorov-Arnold network topology (SVGP-KAN). This approach extends the classical foundations of Linear Stochastic Estimation (LSE) and Spectral Analysis Modal Methods (SAMM) while enabling principled epistemic uncertainty quantification. We perform a systematic comparison of our framework with the classical reconstruction methods as well as Kalman filtering. Using synthetic data from pulsed impingement jet flows, we assess performance across fractional PIV sampling rates ranging from 0.5% to 10%. Evaluation metrics include reconstruction error, generalization gap, structure preservation, and uncertainty calibration. Our SVGP-KAN methods achieve reconstruction accuracy comparable to established methods, while also providing well-calibrated uncertainty estimates that reliably indicate when and where predictions degrade. The results demonstrate a robust, data-driven framework for flow field reconstruction with meaningful uncertainty quantification and offer practical guidance for experimental design in periodic flows.

KANO: Kolmogorov-Arnold Neural Operator for Image Super-Resolution

Authors: Chenyu Li, Danfeng Hong, Bing Zhang, Zhaojie Pan, Jocelyn Chanussot

Abstract: The highly nonlinear degradation process, complex physical interactions, and various sources of uncertainty render single-image Super-resolution (SR) a particularly challenging task. Existing interpretable SR approaches, whether based on prior learning or deep unfolding optimization frameworks, typically rely on black-box deep networks to model latent variables, which leaves the degradation process largely unknown and uncontrollable. Inspired by the Kolmogorov-Arnold theorem (KAT), we for the first time propose a novel interpretable operator, termed Kolmogorov-Arnold Neural Operator (KANO), with the application to image SR. KANO provides a transparent and structured representation of the latent degradation fitting process. Specifically, we employ an additive structure composed of a finite number of B-spline functions to approximate continuous spectral curves in a piecewise fashion. By learning and optimizing the shape parameters of these spline functions within defined intervals, our KANO accurately captures key spectral characteristics, such as local linear trends and the peak-valley structures at nonlinear inflection points, thereby endowing SR results with physical interpretability. Furthermore, through theoretical modeling and experimental evaluations across natural images, aerial photographs, and satellite remote sensing data, we systematically compare multilayer perceptrons (MLPs) and Kolmogorov-Arnold networks (KANs) in handling complex sequence fitting tasks. This comparative study elucidates the respective advantages and limitations of these models in characterizing intricate degradation mechanisms, offering valuable insights for the development of interpretable SR techniques.

2026

January

ABFR-KAN: Kolmogorov-Arnold Networks for Functional Brain Analysis

Authors: Tyler Ward, Abdullah Imran

Abstract: Functional connectivity (FC) analysis, a valuable tool for computer-aided brain disorder diagnosis, traditionally relies on atlas-based parcellation. However, issues relating to selection bias and a lack of regard for subject specificity can arise as a result of such parcellations. Addressing this, we propose ABFR-KAN, a transformer-based classification network that incorporates novel advanced brain function representation components with the power of Kolmogorov-Arnold Networks (KANs) to mitigate structural bias, improve anatomical conformity, and enhance the reliability of FC estimation. Extensive experiments on the ABIDE I dataset, including cross-site evaluation and ablation studies across varying model backbones and KAN configurations, demonstrate that ABFR-KAN consistently outperforms state-of-the-art baselines for autism spectrum distorder (ASD) classification. Our code is available at https://github.com/tbwa233/ABFR-KAN.

Discovering the Gell-Mann-Okubo Formula with Kolmogorov-Arnold Networks

Authors: Jian-Yao He, Xun Chen, Xiao-Yan Zhu, Wen Luo

Abstract: Uncovering physical laws from experimental data is a fundamental goal of theoretical physics. In this work, we apply the spline-based, interpretable Kolmogorov-Arnold Network (KAN) to explore the algebraic structure underlying the baryon octet and decuplet mass spectra. Within a symbolic regression framework and without imposing theoretical priors, KAN autonomously recovers the classical Gell-Mann-Okubo mass relations and accurately extracts the associated SU(3) symmetry-breaking parameters. Compared to conventional fitting approaches, this method achieves comparable predictive accuracy while offering substantially improved interpretability and analytic transparency. Our results demonstrate the potential of KAN as a powerful tool for symbolic discovery in hadron physics and for bridging data-driven modeling with fundamental physical laws.

KAN-AE with Non-Linearity Score and Symbolic Regression for Energy-Efficient Channel Coding

Authors: Anthony Joseph Perre, Parker Huggins, Alphan Sahin

Abstract: In this paper, we investigate Kolmogorov-Arnold network-based autoencoders (KAN-AEs) with symbolic regression (SR) for energy-efficient channel coding. By using SR, we convert KAN-AEs into symbolic expressions, which enables low-complexity implementation and improved energy efficiency at the radios. To further enhance the efficiency, we introduce a new non-linearity score term in the SR process to help select lower-complexity equations when possible. Through numerical simulations, we demonstrate that KAN-AEs achieve competitive BLER performance while improving energy efficiency when paired with SR. We score the energy efficiency of a KAN-AE implementation using the proposed non-linearity metric and compare it to a multi-layer perceptron-based autoencoder (MLP-AE). Our experiment shows that the KAN-AE paired with SR uses 1.38 times less energy than the MLP-AE, supporting that KAN-AEs are a promising choice for energy-efficient deep learning-based channel coding.

Temporal Kolmogorov-Arnold Networks (T-KAN) for High-Frequency Limit Order Book Forecasting: Efficiency, Interpretability, and Alpha Decay

Author: Ahmad Makinde

Abstract: High-Frequency trading (HFT) environments are characterised by large volumes of limit order book (LOB) data, which is notoriously noisy and non-linear. Alpha decay represents a significant challenge, with traditional models such as DeepLOB losing predictive power as the time horizon (k) increases. In this paper, using data from the FI-2010 dataset, we introduce Temporal Kolmogorov-Arnold Networks (T-KAN) to replace the fixed, linear weights of standard LSTMs with learnable B-spline activation functions. This allows the model to learn the ‘shape’ of market signals as opposed to just their magnitude. This resulted in a 19.1% relative improvement in the F1-score at the k = 100 horizon. The efficacy of T-KAN networks cannot be understated, producing a 132.48% return compared to the -82.76% DeepLOB drawdown under 1.0 bps transaction costs. In addition to this, the T-KAN model proves quite interpretable, with the ‘dead-zones’ being clearly visible in the splines. The T-KAN architecture is also uniquely optimized for low-latency FPGA implementation via High level Synthesis (HLS). The code for the experiments in this project can be found at https://github.com/AhmadMak/Temporal-Kolmogorov-Arnold-Networks-T-KAN-for-High-Frequency-Limit-Order-Book-Forecasting.

inRAN: Interpretable Online Bayesian Learning for Network Automation in Open Radio Access Networks

Authors: Ming Zhao, Yuru Zhang, Qiang Liu, Ahan Kak, Nakjung Choi

Abstract: Emerging AI/ML techniques have been showing great potential in automating network control in open radio access networks (Open RAN). However, existing approaches heavily rely on blackbox policies parameterized by deep neural networks, which inherently lack interpretability, explainability, and transparency, and create substantial obstacles in practical network deployment. In this paper, we propose inRAN, a novel interpretable online Bayesian learning framework for network automation in Open RAN. The core idea is to integrate interpretable surrogate models and safe optimization solvers to continually optimize control actions, while adapting to non-stationary dynamics in real-world networks. We achieve the inRAN framework with three key components: 1) an interpretable surrogate model via ensembling Kolmogorov-Arnold Networks (KANs); 2) safe optimization solvers via integrating genetic search and trust-region descent method; 3) an online dynamics tracker via continual model learning and adaptive threshold offset. We implement inRAN in an end-to-end O-RAN-compliant network testbed, and conduct extensive over-the-air experiments with the focused use case of network slicing. The results show that, inRAN substantially outperforms state-of-the-art works, by guaranteeing the chance-based constraint with a 92.67% assurance ratio with comparative resource usage throughout the online network control, under unforeseeable time-evolving network dynamics.

LUT-KAN: Segment-wise LUT Quantization for Fast KAN Inference

Author: Oleksandr Kuznetsov

Abstract: Kolmogorov–Arnold Networks (KAN) replace scalar weights by learnable univariate functions, often implemented with B-splines. This design can be accurate and interpretable, but it makes inference expensive on CPU because each layer requires many spline evaluations. Standard quantization toolchains are also hard to apply because the main computation is not a matrix multiply but repeated spline basis evaluation. This paper introduces LUT-KAN, a segment-wise lookup-table (LUT) compilation and quantization method for PyKAN-style KAN layers. LUT-KAN converts each edge function into a per-segment LUT with affine int8/uint8 quantization and linear interpolation. The method provides an explicit and reproducible inference contract, including boundary conventions and out-of-bounds (OOB) policies. We propose an ``honest baseline’’ methodology for speed evaluation: B-spline evaluation and LUT evaluation are compared under the same backend optimization (NumPy vs NumPy and Numba vs Numba), which separates representation gains from vectorization and JIT effects. Experiments include controlled sweeps over LUT resolution L in 16, 32, 64, 128 and two quantization schemes (symmetric int8 and asymmetric uint8). We report accuracy, speed, and memory metrics with mean and standard deviation across multiple seeds. A two-by-two OOB robustness matrix evaluates behavior under different boundary modes and OOB policies. In a case study, we compile a trained KAN model for DoS attack detection (CICIDS2017 pipeline) into LUT artifacts. The compiled model preserves classification quality (F1 drop below 0.0002) while reducing steady-state CPU inference latency by 12x under NumPy and 10x under Numba backends (honest baseline). The memory overhead is approximately 10x at L=64. All code and artifacts are publicly available with fixed release tags for reproducibility.

Investigation into respiratory sound classification for an imbalanced data set using hybrid LSTM-KAN architectures

Authors: Nithinkumar K. V, Anand R

Abstract: Respiratory sounds captured via auscultation contain critical clues for diagnosing pulmonary conditions. Automated classification of these sounds faces challenges due to subtle acoustic differences and severe class imbalance in clinical datasets. This study investigates respiratory sound classification with a focus on mitigating pronounced class imbalance. We propose a hybrid deep learning model that combines a Long Short-Term Memory (LSTM) network for sequential feature encoding with a Kolmogorov-Arnold Network (KAN) for classification. The model is integrated with a comprehensive feature extraction pipeline and targeted imbalance mitigation strategies. Experiments were conducted on a public respiratory sound database comprising six classes with a highly skewed distribution. Techniques such as focal loss, class-specific data augmentation, and Synthetic Minority Over-sampling Technique (SMOTE) were employed to enhance minority class recognition. The proposed Hybrid LSTM-KAN model achieves an overall accuracy of 94.6 percent and a macro-averaged F1 score of 0.703, despite the dominant COPD class accounting for over 86 percent of the data. Improved detection performance is observed for minority classes compared to baseline approaches, demonstrating the effectiveness of the proposed architecture for imbalanced respiratory sound classification.

Kolmogorov-Arnold Networks-Based Tolerance-Aware Manufacturability Assessment Integrating Design-for-Manufacturing Principles

Authors: Masoud Deylami, Negar Izadipour, Adel Alaeddini

Abstract: Manufacturability assessment is a critical step in bridging the persistent gap between design and production. While artificial intelligence (AI) has been widely applied to this task, most existing frameworks rely on geometry-driven methods that require extensive preprocessing, suffer from information loss, and offer limited interpretability. This study proposes a methodology that evaluates manufacturability directly from parametric design features, enabling explicit incorporation of dimensional tolerances without requiring computer-aided design (CAD) processing. The approach employs Kolmogorov-Arnold Networks (KANs) to learn functional relationships between design parameters, tolerances, and manufacturability outcomes. A synthetic dataset of 300,000 labeled designs is generated to evaluate performance across three representative scenarios: hole drilling, pocket milling, and combined drilling-milling, while accounting for machining constraints and design-for-manufacturing (DFM) rules. Benchmarking against fourteen machine learning (ML) and deep learning (DL) models shows that KAN achieves the highest performance in all scenarios, with AUC values of 0.9919 for drilling, 0.9841 for milling, and 0.9406 for the combined case. The proposed framework provides high interpretability through spline-based functional visualizations and latent-space projections, enabling identification of the design and tolerance parameters that most strongly influence manufacturability. An industrial case study further demonstrates how the framework enables iterative, parameter-level design modifications that transform a non-manufacturable component into a manufacturable one.

Representing Sounds as Neural Amplitude Fields: A Benchmark of Coordinate-MLPs and A Fourier Kolmogorov-Arnold Framework

Authors: Linfei Li, Lin Zhang, Zhong Wang, Fengyi Zhang, Zelin Li, Ying Shen

Abstract: Although Coordinate-MLP-based implicit neural representations have excelled in representing radiance fields, 3D shapes, and images, their application to audio signals remains underexplored. To fill this gap, we investigate existing implicit neural representations, from which we extract 3 types of positional encoding and 16 commonly used activation functions. Through combinatorial design, we establish the first benchmark for Coordinate-MLPs in audio signal representations. Our benchmark reveals that Coordinate-MLPs require complex hyperparameter tuning and frequency-dependent initialization, limiting their robustness. To address these issues, we propose Fourier-ASR, a novel framework based on the Fourier series theorem and the Kolmogorov-Arnold representation theorem. Fourier-ASR introduces Fourier Kolmogorov-Arnold Networks (Fourier-KAN), which leverage periodicity and strong nonlinearity to represent audio signals, eliminating the need for additional positional encoding. Furthermore, a Frequency-adaptive Learning Strategy (FaLS) is proposed to enhance the convergence of Fourier-KAN by capturing high-frequency components and preventing overfitting of low-frequency signals. Extensive experiments conducted on natural speech and music datasets reveal that: (1) well-designed positional encoding and activation functions in Coordinate-MLPs can effectively improve audio representation quality; and (2) Fourier-ASR can robustly represent complex audio signals without extensive hyperparameter tuning. Looking ahead, the continuity and infinite resolution of implicit audio representations make our research highly promising for tasks such as audio compression, synthesis, and generation. The source code will be released publicly to ensure reproducibility. The code is available at https://github.com/lif314/Fourier-ASR.

Free-RBF-KAN: Kolmogorov-Arnold Networks with Adaptive Radial Basis Functions for Efficient Function Learning

Authors: Shao-Ting Chiu, Siu Wun Cheung, Ulisses Braga-Neto, Chak Shing Lee, Rui Peng Li

Abstract: Kolmogorov-Arnold Networks (KANs) offer a promising framework for approximating complex nonlinear functions, yet the original B-spline formulation suffers from significant computational overhead due to De Boor algorithm. While recent RBF-based variants improve efficiency, they often sacrifice the approximation accuracy inherent in the original spline-based design. To bridge this gap, we propose Free-RBF-KAN, an architecture that integrates adaptive learning grids and trainable smoothness parameters to enable expressive, high-resolution function approximation. Our method utilizes learnable RBF shapes that dynamically align with activation patterns, and we provide the first formal universal approximation proof for the RBF-KAN family. Empirical evaluations across multiscale regression, physics-informed PDEs, and operator learning demonstrate that Free-RBF-KAN can achieve accuracy comparable to its B-spline counterparts while delivering significantly faster training and inference. These results establish Free-RBF-KAN as an efficient and adaptive alternative for high-dimensional structured modeling tasks.

An Efficient Additive Kolmogorov-Arnold Transformer for Point-Level Maize Localization in Unmanned Aerial Vehicle Imagery

Authors: Fei Li, Lang Qiao, Jiahao Fan, Yijia Xu, Shawn M. Kaeppler, Zhou Zhang

Abstract: High-resolution UAV photogrammetry has become a key technology for precision agriculture, enabling centimeter-level crop monitoring and point-level plant localization. However, point-level maize localization in UAV imagery remains challenging due to (1) extremely small object-to-pixel ratios, typically less than 0.1%, (2) prohibitive computational costs of quadratic attention on ultra-high-resolution images larger than 3000 x 4000 pixels, and (3) agricultural scene-specific complexities such as sparse object distribution and environmental variability that are poorly handled by general-purpose vision models. To address these challenges, we propose the Additive Kolmogorov-Arnold Transformer (AKT), which replaces conventional multilayer perceptrons with Pade Kolmogorov-Arnold Network (PKAN) modules to enhance functional expressivity for small-object feature extraction, and introduces PKAN Additive Attention (PAA) to model multiscale spatial dependencies with reduced computational complexity. In addition, we present the Point-based Maize Localization (PML) dataset, consisting of 1,928 high-resolution UAV images with approximately 501,000 point annotations collected under real field conditions. Extensive experiments show that AKT achieves an average F1-score of 62.8%, outperforming state-of-the-art methods by 4.2%, while reducing FLOPs by 12.6% and improving inference throughput by 20.7%. For downstream tasks, AKT attains a mean absolute error of 7.1 in stand counting and a root mean square error of 1.95-1.97 cm in interplant spacing estimation. These results demonstrate that integrating Kolmogorov-Arnold representation theory with efficient attention mechanisms offers an effective framework for high-resolution agricultural remote sensing.

LUT-Compiled Kolmogorov-Arnold Networks for Lightweight DoS Detection on IoT Edge Devices

Author: Oleksandr Kuznetsov

Abstract: Denial-of-Service (DoS) attacks pose a critical threat to Internet of Things (IoT) ecosystems, yet deploying effective intrusion detection on resource-constrained edge devices remains challenging. Kolmogorov-Arnold Networks (KANs) offer a compact alternative to Multi-Layer Perceptrons (MLPs) by placing learnable univariate spline functions on edges rather than fixed activations on nodes, achieving competitive accuracy with fewer parameters. However, runtime B-spline evaluation introduces significant computational overhead unsuitable for latency-critical IoT applications. We propose a lookup table (LUT) compilation pipeline that replaces expensive spline computations with precomputed quantized tables and linear interpolation, dramatically reducing inference latency while preserving detection quality. Our lightweight KAN model (50K parameters, 0.19~MB) achieves 99.0\% accuracy on the CICIDS2017 DoS dataset. After LUT compilation with resolution $L=8$, the model maintains 98.96\% accuracy (F1 degradation $<0.0004$) while achieving $\mathbf{68\times}$ speedup at batch size 256 and over $\mathbf{5000\times}$ speedup at batch size 1, with only $2\times$ memory overhead. We provide comprehensive evaluation across LUT resolutions, quantization schemes, and out-of-bounds policies, establishing clear Pareto frontiers for accuracy-latency-memory trade-offs. Our results demonstrate that LUT-compiled KANs enable real-time DoS detection on CPU-only IoT gateways with deterministic inference latency and minimal resource footprint.

Trustworthy Longitudinal Brain MRI Completion: A Deformation-Based Approach with KAN-Enhanced Diffusion Model

Authors: Tianli Tao, Ziyang Wang, Delong Yang, Han Zhang, Le Zhang

Abstract: Longitudinal brain MRI is essential for lifespan study, yet high attrition rates often lead to missing data, complicating analysis. Deep generative models have been explored, but most rely solely on image intensity, leading to two key limitations: 1) the fidelity or trustworthiness of the generated brain images are limited, making downstream studies questionable; 2) the usage flexibility is restricted due to fixed guidance rooted in the model structure, restricting full ability to versatile application scenarios. To address these challenges, we introduce DF-DiffCom, a Kolmogorov-Arnold Networks (KAN)-enhanced diffusion model that smartly leverages deformation fields for trustworthy longitudinal brain image completion. Trained on OASIS-3, DF-DiffCom outperforms state-of-the-art methods, improving PSNR by 5.6% and SSIM by 0.12. More importantly, its modality-agnostic nature allows smooth extension to varied MRI modalities, even to attribute maps such as brain tissue segmentation results.

Learning Ecological and Epidemic Processes using Neural ODEs, Kolmogorov-Arnold Network ODEs and SINDy

Authors: Maria Vasilyeva, Zheng Wei, Kelum Gajamannage, Hyangim Ji, Aleksei Krasnikov, Alexey Sadovski

Abstract: We consider epidemic and ecological models to investigate their coupled dynamics. Starting with the classical Susceptible-Infected-Recovered (SIR) model for basic epidemic behavior and the predator-prey (Lotka-Volterra, LV) system for ecological interactions, we then combine these frameworks into a coupled Lotka-Volterra-Susceptible-Infected-Susceptible (LVSIS) model. The resulting system consists of four differential equations describing the evolution of susceptible and infected prey and predator populations, incorporating ecological interactions, disease transmission, and spatial dispersal. To learn the underlying dynamics directly from data, we employ several data-driven modeling frameworks: Neural Ordinary Differential Equations (Neural ODEs), Kolmogorov-Arnold Network Ordinary Differential Equations (KANODEs), and Sparse Identification of Nonlinear Dynamics (SINDy). Numerical experiments based on synthetic data are conducted to investigate the learning ability of these models in capturing the epidemic and ecological behavior. We further extend our approach to spatio-temporal models, aiming to uncover hidden local couplings.

A coupled Kolmogorov-Arnold Network and Level-Set framework for evolving interfaces

Authors: Tarus Pande, V M S K Minnikanti, Shyamprasad Karagadde

Abstract: Kolmogorov-Arnold Networks (KANs) require significantly smaller architectures compared to multilayer perceptron (MLP)-based approaches, while retaining expressive power through spline-based activations. Moving boundary problems are ubiquitous in physical systems, whose numerical solutions are quite complex. We propose a shallow KAN framework combined with a Level-set formulation that directly approximates the temperature distribution $T(\mathbf{x},t)$ and the moving interface $Γ(t)$, enforcing the governing PDEs, phase equilibrium, and Stefan condition through physics-informed residuals. Numerical experiments in one and two dimensions show that the framework achieves accurate reconstructions of both temperature fields and interface dynamics, highlighting the potential of KANs as a compact and efficient alternative for moving boundary PDEs. First, we validate the model with semi-infinite analytical solutions. Subsequently, the model is extended to 2D using a level-set based formulation for interface propagation, which is solved within the KAN framework. This work demonstrates that KANs are capable of solving complex moving boundary problems without the need for measurement data.

Kolmogorov Arnold Networks and Multi-Layer Perceptrons: A Paradigm Shift in Neural Modelling

Authors: Aradhya Gaonkar, Nihal Jain, Vignesh Chougule, Nikhil Deshpande, Sneha Varur, Channabasappa Muttal

Abstract: The research undertakes a comprehensive comparative analysis of Kolmogorov-Arnold Networks (KAN) and Multi-Layer Perceptrons (MLP), highlighting their effectiveness in solving essential computational challenges like nonlinear function approximation, time-series prediction, and multivariate classification. Rooted in Kolmogorov’s representation theorem, KANs utilize adaptive spline-based activation functions and grid-based structures, providing a transformative approach compared to traditional neural network frameworks. Utilizing a variety of datasets spanning mathematical function estimation (quadratic and cubic) to practical uses like predicting daily temperatures and categorizing wines, the proposed research thoroughly assesses model performance via accuracy measures like Mean Squared Error (MSE) and computational expense assessed through Floating Point Operations (FLOPs). The results indicate that KANs reliably exceed MLPs in every benchmark, attaining higher predictive accuracy with significantly reduced computational costs. Such an outcome highlights their ability to maintain a balance between computational efficiency and accuracy, rendering them especially beneficial in resource-limited and real-time operational environments. By elucidating the architectural and functional distinctions between KANs and MLPs, the paper provides a systematic framework for selecting the most suitable neural architectures for specific tasks. Furthermore, the proposed study highlights the transformative capabilities of KANs in progressing intelligent systems, influencing their use in situations that require both interpretability and computational efficiency.

KANHedge: Efficient Hedging of High-Dimensional Options Using Kolmogorov-Arnold Network-Based BSDE Solver

Authors: Rushikesh Handal, Masanori Hirano

Abstract: High-dimensional option pricing and hedging present significant challenges in quantitative finance, where traditional PDE-based methods struggle with the curse of dimensionality. The BSDE framework offers a computationally efficient alternative to PDE-based methods, and recently proposed deep BSDE solvers, generally utilizing conventional Multi-Layer Perceptrons (MLPs), build upon this framework to provide a scalable alternative to numerical BSDE solvers. In this research, we show that although such MLP-based deep BSDEs demonstrate promising results in option pricing, there remains room for improvement regarding hedging performance. To address this issue, we introduce KANHedge, a novel BSDE-based hedger that leverages Kolmogorov-Arnold Networks (KANs) within the BSDE framework. Unlike conventional MLP approaches that use fixed activation functions, KANs employ learnable B-spline activation functions that provide enhanced function approximation capabilities for continuous derivatives. We comprehensively evaluate KANHedge on both European and American basket options across multiple dimensions and market conditions. Our experimental results demonstrate that while KANHedge and MLP achieve comparable pricing accuracy, KANHedge provides improved hedging performance. Specifically, KANHedge achieves considerable reductions in hedging cost metrics, demonstrating enhanced risk control capabilities.

An Efficient and Explainable KAN Framework for Wireless Radiation Field Prediction

Authors: Jingzhou Shen, Xuyu Wang

Abstract: Modeling wireless channels accurately remains a challenge due to environmental variations and signal uncertainties. Recent neural networks can learn radio frequency~(RF) signal propagation patterns, but they process each voxel on the ray independently, without considering global context or environmental factors. Our paper presents a new approach that learns comprehensive representations of complete rays rather than individual points, capturing more detailed environmental features. We integrate a Kolmogorov-Arnold network (KAN) architecture with transformer modules to achieve better performance across realistic and synthetic scenes while maintaining computational efficiency. Our experimental results show that this approach outperforms existing methods in various scenarios. Ablation studies confirm that each component of our model contributes to its effectiveness. Additional experiments provide clear explanations for our model’s performance.

Learning Nonlinear Heterogeneity in Physical Kolmogorov-Arnold Networks

Authors: Fabiana Taglietti, Andrea Pulici, Maxwell Roxburgh, Gabriele Seguini, Ian Vidamour, Stephan Menzel, Edoardo Franco, Michele Laus, Eleni Vasilaki, Michele Perego, Thomas J. Hayward, Marco Fanciulli, Jack C. Gartside

Abstract: Physical neural networks typically train linear synaptic weights while treating device nonlinearities as fixed. We show the opposite - by training the synaptic nonlinearity itself, as in Kolmogorov-Arnold Network (KAN) architectures, we yield markedly higher task performance per physical resource and improved performance-parameter scaling than conventional linear weight-based networks, demonstrating ability of KAN topologies to exploit reconfigurable nonlinear physical dynamics. We experimentally realise physical KANs in silicon-on-insulator devices we term ‘Synaptic Nonlinear Elements’ (SYNEs), operating at room temperature, microampere currents, 2 MHz speeds and ~750 fJ per nonlinear operation, with no observed degradation over 10^13 measurements and months-long timescales. We demonstrate nonlinear function regression, classification, and prediction of Li-Ion battery dynamics from noisy real-world multi-sensor data. Physical KANs outperform equivalently-parameterised software multilayer perceptron networks across all tasks, with up to two orders of magnitude fewer parameters, and two orders of magnitude fewer devices than linear weight based physical networks. These results establish learned physical nonlinearity as a hardware-native computational primitive for compact and efficient learning systems, and SYNE devices as effective substrates for heterogenous nonlinear computing.

AI-Based Culvert-Sewer Inspection

Author: Christina Thrainer

Abstract: Culverts and sewer pipes are critical components of drainage systems, and their failure can lead to serious risks to public safety and the environment. In this thesis, we explore methods to improve automated defect segmentation in culverts and sewer pipes. Collecting and annotating data in this field is cumbersome and requires domain knowledge. Having a large dataset for structural defect detection is therefore not feasible. Our proposed methods are tested under conditions with limited annotated data to demonstrate applicability to real-world scenarios. Overall, this thesis proposes three methods to significantly enhance defect segmentation and handle data scarcity. This can be addressed either by enhancing the training data or by adjusting a models architecture. First, we evaluate preprocessing strategies, including traditional data augmentation and dynamic label injection. These techniques significantly improve segmentation performance, increasing both Intersection over Union (IoU) and F1 score. Second, we introduce FORTRESS, a novel architecture that combines depthwise separable convolutions, adaptive Kolmogorov-Arnold Networks (KAN), and multi-scale attention mechanisms. FORTRESS achieves state-of-the-art performance on the culvert sewer pipe defect dataset, while significantly reducing the number of trainable parameters, as well as its computational cost. Finally, we investigate few-shot semantic segmentation and its applicability to defect detection. Few-shot learning aims to train models with only limited data available. By employing a bidirectional prototypical network with attention mechanisms, the model achieves richer feature representations and achieves satisfactory results across evaluation metrics.

A Dynamic Framework for Grid Adaptation in Kolmogorov-Arnold Networks

Authors: Spyros Rigas, Thanasis Papaioannou, Panagiotis Trakadas, Georgios Alexandridis

Abstract: Kolmogorov-Arnold Networks (KANs) have recently demonstrated promising potential in scientific machine learning, partly due to their capacity for grid adaptation during training. However, existing adaptation strategies rely solely on input data density, failing to account for the geometric complexity of the target function or metrics calculated during network training. In this work, we propose a generalized framework that treats knot allocation as a density estimation task governed by Importance Density Functions (IDFs), allowing training dynamics to determine grid resolution. We introduce a curvature-based adaptation strategy and evaluate it across synthetic function fitting, regression on a subset of the Feynman dataset and different instances of the Helmholtz PDE, demonstrating that it significantly outperforms the standard input-based baseline. Specifically, our method yields average relative error reductions of 25.3% on synthetic functions, 9.4% on the Feynman dataset, and 23.3% on the PDE benchmark. Statistical significance is confirmed via Wilcoxon signed-rank tests, establishing curvature-based adaptation as a robust and computationally efficient alternative for KAN training.

LabelKAN – Kolmogorov-Arnold Networks for Inter-Label Learning: Avian Community Learning

Authors: Marc Grimson, Joshua Fan, Courtney L. Davis, Dylan van Bramer, Daniel Fink, Carla P. Gomes

Abstract: Global biodiversity loss is accelerating, prompting international efforts such as the Kunming-Montreal Global Biodiversity Framework (GBF) and the United Nations Sustainable Development Goals to direct resources toward halting species declines. A key challenge in achieving this goal is having access to robust methodologies to understand where species occur and how they relate to each other within broader ecological communities. Recent deep learning-based advances in joint species distribution modeling have shown improved predictive performance, but effectively incorporating community-level learning, taking into account species-species relationships in addition to species-environment relationships, remains an outstanding challenge. We introduce LabelKAN, a novel framework based on Kolmogorov-Arnold Networks (KANs) to learn inter-label connections from predictions of each label. When modeling avian species distributions, LabelKAN achieves substantial gains in predictive performance across the vast majority of species. In particular, our method demonstrates strong improvements for rare and difficult-to-predict species, which are often the most important when setting biodiversity targets under frameworks like GBF. These performance gains also translate to more confident predictions of the species spatial patterns as well as more confident predictions of community structure. We illustrate how the LabelKAN leads to qualitative and quantitative improvements with a focused application on the Great Blue Heron, an emblematic species in freshwater ecosystems that has experienced significant population declines across the United States in recent years. Using the LabelKAN framework, we are able to identify communities and species in New York that will be most sensitive to further declines in Great Blue Heron populations.

Time series forecasting with Hahn Kolmogorov-Arnold networks

Authors: Md Zahidul Hasan, A. Ben Hamza, Nizar Bouguila

Abstract: Recent Transformer- and MLP-based models have demonstrated strong performance in long-term time series forecasting, yet Transformers remain limited by their quadratic complexity and permutation-equivariant attention, while MLPs exhibit spectral bias. We propose HaKAN, a versatile model based on Kolmogorov-Arnold Networks (KANs), leveraging Hahn polynomial-based learnable activation functions and providing a lightweight and interpretable alternative for multivariate time series forecasting. Our model integrates channel independence, patching, a stack of Hahn-KAN blocks with residual connections, and a bottleneck structure comprised of two fully connected layers. The Hahn-KAN block consists of inter- and intra-patch KAN layers to effectively capture both global and local temporal patterns. Extensive experiments on various forecasting benchmarks demonstrate that our model consistently outperforms recent state-of-the-art methods, with ablation studies validating the effectiveness of its core components.

Learning constitutive laws under explicit strain limits: An interpretable strain-limiting elasticity–Kolmogorov Arnold neural network framework

Authors: Chandana Pati, S. M. Mallikarjunaiah

Abstract: A physically consistent framework for modeling materials with saturating deformation, such as elastomers and biological tissues, is provided by strain-limiting elasticity. Fundamental limitations of classical elasticity are addressed through the enforcement of bounded strains; however, significant challenges for data-driven learning are posed by the strong nonlinearity of these laws. In this work, an interpretable hybrid constitutive modeling framework integrating strain-limiting elasticity (SLE) with Kolmogorov-Arnold Networks (KANs) is proposed to balance mechanical admissibility with data-driven flexibility. The dominant nonlinear response is captured by the SLE backbone, while smooth residual corrections are learned exclusively via a KAN. Essential mechanical principles-including symmetry, monotonicity, and bounded strain-are embedded directly into the model structure to ensure physical admissibility. The framework is assessed on synthetic benchmarks, where near-exact recovery is achieved in smooth regimes and consistency is retained under sharp transitions. Application to Treloar’s rubber elasticity data demonstrates systematic improvement in stress-stretch agreement while preserving explicit strain limits. A regime-based analysis reveals a transparent trade-off between data fidelity and mechanical admissibility, demonstrating that deviations arise from deliberately imposed physical restrictions rather than unconstrained model expressivity. This SLE-KAN framework offers a robust, physics-consistent alternative to black-box neural networks for constitutive modeling.

Fixed Aggregation Features Can Rival GNNs

Authors: Celia Rubio-Madrigal, Rebekka Burkholz

Abstract: Graph neural networks (GNNs) are widely believed to excel at node representation learning through trainable neighborhood aggregations. We challenge this view by introducing Fixed Aggregation Features (FAFs), a training-free approach that transforms graph learning tasks into tabular problems. This simple shift enables the use of well-established tabular methods, offering strong interpretability and the flexibility to deploy diverse classifiers. Across 14 benchmarks, well-tuned multilayer perceptrons trained on FAFs rival or outperform state-of-the-art GNNs and graph transformers on 12 tasks – often using only mean aggregation. The only exceptions are the Roman Empire and Minesweeper datasets, which typically require unusually deep GNNs. To explain the theoretical possibility of non-trainable aggregations, we connect our findings to Kolmogorov-Arnold representations and discuss when mean aggregation can be sufficient. In conclusion, our results call for (i) richer benchmarks benefiting from learning diverse neighborhood aggregations, (ii) strong tabular baselines as standard, and (iii) employing and advancing tabular models for graph data to gain new insights into related tasks.

Kolmogorov-Arnold Networks Applied to Materials Property Prediction

Authors: Ryan Jacobs, Lane E. Schultz, Dane Morgan

Abstract: Kolmogorov-Arnold Networks (KANs) were proposed as an alternative to traditional neural network architectures based on multilayer perceptrons (MLP-NNs). The potential advantages of KANs over MLP-NNs, including significantly enhanced parameter efficiency and increased interpretability, make them a promising new regression model in supervised machine learning problems. We apply KANs to prediction of materials properties, focusing on a diverse set of 33 properties consisting of both experimental and calculated data. We compare the KAN results to random forest, a method that generally gives excellent performance on a wide range of properties predictions with very little optimization. The KANs were worse, on par, or better than random forest about 35%, 60%, and 5% of the time, respectively, and KANs are in practice more difficult to fit than random forest. By tuning the network architecture, we found property fits often resulted in 10-20% lower errors compared to the standard KAN, and typically gave results comparable to random forest. In the specific context of predicting reactor pressure vessel transition temperature shifts, we explored the parameter efficiency and the interpretable power of KANs by comparing predictions of simple KAN models (e.g., < 50 parameters) and closed-form expressions suggested by the KAN fits to previously published deep MLP-NNs and hand-tuned models created using domain expertise of embrittlement physics. We found that simple KAN models and the resulting closed-form expressions produce prediction errors on par with established hand-tuned models with a comparable number of parameters, and required essentially no domain expertise to produce. These findings reinforce the potential applicability of KANs for machine learning in materials science and suggest that KANs should be explored as a regression model for prediction of materials properties.

Vision KAN: Towards an Attention-Free Backbone for Vision with Kolmogorov-Arnold Networks

Authors: Zhuoqin Yang, Jiansong Zhang, Xiaoling Luo, Xu Wu, Zheng Lu, Linlin Shen

Abstract: Attention mechanisms have become a key module in modern vision backbones due to their ability to model long-range dependencies. However, their quadratic complexity in sequence length and the difficulty of interpreting attention weights limit both scalability and clarity. Recent attention-free architectures demonstrate that strong performance can be achieved without pairwise attention, motivating the search for alternatives. In this work, we introduce Vision KAN (ViK), an attention-free backbone inspired by the Kolmogorov-Arnold Networks. At its core lies MultiPatch-RBFKAN, a unified token mixer that combines (a) patch-wise nonlinear transform with Radial Basis Function-based KANs, (b) axis-wise separable mixing for efficient local propagation, and (c) low-rank global mapping for long-range interaction. Employing as a drop-in replacement for attention modules, this formulation tackles the prohibitive cost of full KANs on high-resolution features by adopting a patch-wise grouping strategy with lightweight operators to restore cross-patch dependencies. Experiments on ImageNet-1K show that ViK achieves competitive accuracy with linear complexity, demonstrating the potential of KAN-based token mixing as an efficient and theoretically grounded alternative to attention.

Optimization, Generalization and Differential Privacy Bounds for Gradient Descent on Kolmogorov-Arnold Networks

Authors: Puyu Wang, Junyu Zhou, Philipp Liznerski, Marius Kloft

Abstract: Kolmogorov–Arnold Networks (KANs) have recently emerged as a structured alternative to standard MLPs, yet a principled theory for their training dynamics, generalization, and privacy properties remains limited. In this paper, we analyze gradient descent (GD) for training two-layer KANs and derive general bounds that characterize their training dynamics, generalization, and utility under differential privacy (DP). As a concrete instantiation, we specialize our analysis to logistic loss under an NTK-separable assumption, where we show that polylogarithmic network width suffices for GD to achieve an optimization rate of order $1/T$ and a generalization rate of order $1/n$, with $T$ denoting the number of GD iterations and $n$ the sample size. In the private setting, we characterize the noise required for $(ε,δ)$-DP and obtain a utility bound of order $\sqrt{d}/(nε)$ (with $d$ the input dimension), matching the classical lower bound for general convex Lipschitz problems. Our results imply that polylogarithmic width is not only sufficient but also necessary under differential privacy, revealing a qualitative gap between non-private (sufficiency only) and private (necessity also emerges) training regimes. Experiments further illustrate how these theoretical insights can guide practical choices, including network width selection and early stopping.

Agile Reinforcement Learning through Separable Neural Architecture

Authors: Rajib Mostakim, Reza T. Batley, Sourav Saha

Abstract: Deep reinforcement learning (RL) is increasingly deployed in resource-constrained environments, yet the go-to function approximators - multilayer perceptrons (MLPs) - are often parameter-inefficient due to an imperfect inductive bias for the smooth structure of many value functions. This mismatch can also hinder sample efficiency and slow policy learning in this capacity-limited regime. Although model compression techniques exist, they operate post-hoc and do not improve learning efficiency. Recent spline-based separable architectures - such as Kolmogorov-Arnold Networks (KANs) - have been shown to offer parameter efficiency but are widely reported to exhibit significant computational overhead, especially at scale. In seeking to address these limitations, this work introduces SPAN (SPline-based Adaptive Networks), a novel function approximation approach to RL. SPAN adapts the low rank KHRONOS framework by integrating a learnable preprocessing layer with a separable tensor product B-spline basis. SPAN is evaluated across discrete (PPO) and high-dimensional continuous (SAC) control tasks, as well as offline settings (Minari/D4RL). Empirical results demonstrate that SPAN achieves a 30-50% improvement in sample efficiency and 1.3-9 times higher success rates across benchmarks compared to MLP baselines. Furthermore, SPAN demonstrates superior anytime performance and robustness to hyperparameter variations, suggesting it as a viable, high performance alternative for learning intrinsically efficient policies in resource-limited settings.

February

KAN We Flow? Advancing Robotic Manipulation with 3D Flow Matching via KAN & RWKV

Authors: Zhihao Chen, Yiyuan Ge, Ziyang Wang

Abstract: Diffusion-based visuomotor policies excel at modeling action distributions but are inference-inefficient, since recursively denoising from noise to policy requires many steps and heavy UNet backbones, which hinders deployment on resource-constrained robots. Flow matching alleviates the sampling burden by learning a one-step vector field, yet prior implementations still inherit large UNet-style architectures. In this work, we present KAN-We-Flow, a flow-matching policy that draws on recent advances in Receptance Weighted Key Value (RWKV) and Kolmogorov-Arnold Networks (KAN) from vision to build a lightweight and highly expressive backbone for 3D manipulation. Concretely, we introduce an RWKV-KAN block: an RWKV first performs efficient time/channel mixing to propagate task context, and a subsequent GroupKAN layer applies learnable spline-based, groupwise functional mappings to perform feature-wise nonlinear calibration of the action mapping on RWKV outputs. Moreover, we introduce an Action Consistency Regularization (ACR), a lightweight auxiliary loss that enforces alignment between predicted action trajectories and expert demonstrations via Euler extrapolation, providing additional supervision to stabilize training and improve policy precision. Without resorting to large UNets, our design reduces parameters by 86.8\%, maintains fast runtime, and achieves state-of-the-art success rates on Adroit, Meta-World, and DexArt benchmarks. Our project page can be viewed in \href{https://zhihaochen-2003.github.io/KAN-We-Flow.github.io/}{\textcolor{red}{link}}

The Enhanced Physics-Informed Kolmogorov-Arnold Networks: Applications of Newton’s Laws in Financial Deep Reinforcement Learning (RL) Algorithms

Authors: Trang Thoi, Hung Tran, Tram Thoi, Huaiyang Zhong

Abstract: Deep Reinforcement Learning (DRL), a subset of machine learning focused on sequential decision-making, has emerged as a powerful approach for tackling financial trading problems. In finance, DRL is commonly used either to generate discrete trade signals or to determine continuous portfolio allocations. In this work, we propose a novel reinforcement learning framework for portfolio optimization that incorporates Physics-Informed Kolmogorov-Arnold Networks (PIKANs) into several DRL algorithms. The approach replaces conventional multilayer perceptrons with Kolmogorov-Arnold Networks (KANs) in both actor and critic components-utilizing learnable B-spline univariate functions to achieve parameter-efficient and more interpretable function approximation. During actor updates, we introduce a physics-informed regularization loss that promotes second-order temporal consistency between observed return dynamics and the action-induced portfolio adjustments. The proposed framework is evaluated across three equity markets-China, Vietnam, and the United States, covering both emerging and developed economies. Across all three markets, PIKAN-based agents consistently deliver higher cumulative and annualized returns, superior Sharpe and Calmar ratios, and more favorable drawdown characteristics compared to both standard DRL baselines and classical online portfolio-selection methods. This yields more stable training, higher Sharpe ratios, and superior performance compared to traditional DRL counterparts. The approach is particularly valuable in highly dynamic and noisy financial markets, where conventional DRL often suffers from instability and poor generalization.

MGKAN: Predicting Asymmetric Drug-Drug Interactions via a Multimodal Graph Kolmogorov-Arnold Network

Authors: Kunyi Fan, Mengjie Chen, Longlong Li, Cunquan Qu

Abstract: Predicting drug-drug interactions (DDIs) is essential for safe pharmacological treatments. Previous graph neural network (GNN) models leverage molecular structures and interaction networks but mostly rely on linear aggregation and symmetric assumptions, limiting their ability to capture nonlinear and heterogeneous patterns. We propose MGKAN, a Graph Kolmogorov-Arnold Network that introduces learnable basis functions into asymmetric DDI prediction. MGKAN replaces conventional MLP transformations with KAN-driven basis functions, enabling more expressive and nonlinear modeling of drug relationships. To capture pharmacological dependencies, MGKAN integrates three network views-an asymmetric DDI network, a co-interaction network, and a biochemical similarity network-with role-specific embeddings to preserve directional semantics. A fusion module combines linear attention and nonlinear transformation to enhance representational capacity. On two benchmark datasets, MGKAN outperforms seven state-of-the-art baselines. Ablation studies and case studies confirm its predictive accuracy and effectiveness in modeling directional drug effects.

PINN-Based Kolmogorov-Arnold Networks with RAR-D Adaptive Sampling for Solving Elliptic Interface Problems

Authors: Zijuan Xin, Chenyao Wang, Feng Shi, Yizhong Sun

Abstract: Physics-Informed Neural Networks (PINNs) have become a popular and powerful framework for solving partial differential equations (PDEs), leveraging neural networks to approximate solutions while embedding PDE constraints, boundary conditions, and interface jump conditions directly into the loss function. However, most existing PINN approaches are based on multilayer perceptrons (MLPs), which may require large network sizes and extensive training to achieve high accuracy, especially for complex interface problems. In this work, we propose a novel PINN architecture based on Kolmogorov-Arnold Networks (KANs), which offer greater flexibility in choosing activation functions and can represent functions with fewer parameters. Specifically, we introduce a dual KANs structure that couples two KANs across subdomains and explicitly enforces interface conditions. To further boost training efficiency and convergence, we integrate the RAR-D adaptive sampling strategy to dynamically refine training points. Numerical experiments on the elliptic interface problems yield more uniform error distributions across the computational domain, which demonstrates that our PINN-based KANs achieve superior accuracy with significantly smaller network sizes and faster convergence compared to standard PINNs.

Ultrafast On-chip Online Learning via Spline Locality in Kolmogorov-Arnold Networks

Authors: Duc Hoang, Aarush Gupta, Philip Harris

Abstract: Ultrafast online learning is essential for high-frequency systems, such as controls for quantum computing and nuclear fusion, where adaptation must occur on sub-microsecond timescales. Meeting these requirements demands low-latency, fixed-precision computation under strict memory constraints, a regime in which conventional Multi-Layer Perceptrons (MLPs) are both inefficient and numerically unstable. We identify key properties of Kolmogorov-Arnold Networks (KANs) that align with these constraints. Specifically, we show that: (i) KAN updates exploiting B-spline locality are sparse, enabling superior on-chip resource scaling, and (ii) KANs are inherently robust to fixed-point quantization. By implementing fixed-point online training on Field-Programmable Gate Arrays (FPGAs), a representative platform for on-chip computation, we demonstrate that KAN-based online learners are significantly more efficient and expressive than MLPs across a range of low-latency and resource-constrained tasks. To our knowledge, this work is the first to demonstrate model-free online learning at sub-microsecond latencies.

SurvKAN: A Fully Parametric Survival Model Based on Kolmogorov-Arnold Networks

Authors: Marina Mastroleo, Alberto Archetti, Federico Mastroleo, Matteo Matteucci

Abstract: Accurate prediction of time-to-event outcomes is critical for clinical decision-making, treatment planning, and resource allocation in modern healthcare. While classical survival models such as Cox remain widely adopted in standard practice, they rely on restrictive assumptions, including linear covariate relationships and proportional hazards over time, that often fail to capture real-world clinical dynamics. Recent deep learning approaches like DeepSurv and DeepHit offer improved expressivity but sacrifice interpretability, limiting clinical adoption where trust and transparency are paramount. Hybrid models incorporating Kolmogorov-Arnold Networks (KANs), such as CoxKAN, have begun to address this trade-off but remain constrained by the semi-parametric Cox framework. In this work we introduce SurvKAN, a fully parametric, time-continuous survival model based on KAN architectures that eliminates the proportional hazards constraint. SurvKAN treats time as an explicit input to a KAN that directly predicts the log-hazard function, enabling end-to-end training on the full survival likelihood. Our architecture preserves interpretability through learnable univariate functions that indicate how individual features influence risk over time. Extensive experiments on standard survival benchmarks demonstrate that SurvKAN achieves competitive or superior performance compared to classical and state-of-the-art baselines across concordance and calibration metrics. Additionally, interpretability analyses reveal clinically meaningful patterns that align with medical domain knowledge.

KANFIS: A Neuro-Symbolic Framework for Interpretable and Uncertainty-Aware Learning

Authors: Binbin Yong, Haoran Pei, Jun Shen, Haoran Li, Qingguo Zhou, Zhao Su

Abstract: Adaptive Neuro-Fuzzy Inference System (ANFIS) was designed to combine the learning capabilities of neural network with the reasoning transparency of fuzzy logic. However, conventional ANFIS architectures suffer from structural complexity, where the product-based inference mechanism causes an exponential explosion of rules in high-dimensional spaces. We herein propose the Kolmogorov-Arnold Neuro-Fuzzy Inference System (KANFIS), a compact neuro-symbolic architecture that unifies fuzzy reasoning with additive function decomposition. KANFIS employs an additive aggregation mechanism, under which both model parameters and rule complexity scale linearly with input dimensionality rather than exponentially. Furthermore, KANFIS is compatible with both Type-1 (T1) and Interval Type-2 (IT2) fuzzy logic systems, enabling explicit modeling of uncertainty and ambiguity in fuzzy representations. By using sparse masking mechanisms, KANFIS generates compact and structured rule sets, resulting in an intrinsically interpretable model with clear rule semantics and transparent inference processes. Empirical results demonstrate that KANFIS achieves competitive performance against representative neural and neuro-fuzzy baselines.

TruKAN: Towards More Efficient Kolmogorov-Arnold Networks Using Truncated Power Functions

Authors: Ali Bayeh, Samira Sadaoui, Malek Mouhoub

Abstract: To address the trade-off between computational efficiency and adherence to Kolmogorov-Arnold Network (KAN) principles, we propose TruKAN, a new architecture based on the KAN structure and learnable activation functions. TruKAN replaces the B-spline basis in KAN with a family of truncated power functions derived from k-order spline theory. This change maintains the KAN’s expressiveness while enhancing accuracy and training time. Each TruKAN layer combines a truncated power term with a polynomial term and employs either shared or individual knots. TruKAN exhibits greater interpretability than other KAN variants due to its simplified basis functions and knot configurations. By prioritizing interpretable basis functions, TruKAN aims to balance approximation efficacy with transparency. We develop the TruKAN model and integrate it into an advanced EfficientNet-V2-based framework, which is then evaluated on computer vision benchmark datasets. To ensure a fair comparison, we develop various models: MLP-, KAN-, SineKAN and TruKAN-based EfficientNet frameworks and assess their training time and accuracy across small and deep architectures. The training phase uses hybrid optimization to improve convergence stability. Additionally, we investigate layer normalization techniques for all the models and assess the impact of shared versus individual knots in TruKAN. Overall, TruKAN outperforms other KAN models in terms of accuracy, computational efficiency and memory usage on the complex vision task, demonstrating advantages beyond the limited settings explored in prior KAN studies.

Rational ANOVA Networks

Authors: Jusheng Zhang, Ningyuan Liu, Qinhan Lyu, Jing Yang, Keze Wang

Abstract: Deep neural networks typically treat nonlinearities as fixed primitives (e.g., ReLU), limiting both interpretability and the granularity of control over the induced function class. While recent additive models (like KANs) attempt to address this using splines, they often suffer from computational inefficiency and boundary instability. We propose the Rational-ANOVA Network (RAN), a foundational architecture grounded in functional ANOVA decomposition and Padé-style rational approximation. RAN models f(x) as a composition of main effects and sparse pairwise interactions, where each component is parameterized by a stable, learnable rational unit. Crucially, we enforce a strictly positive denominator, which avoids poles and numerical instability while capturing sharp transitions and near-singular behaviors more efficiently than polynomial bases. This ANOVA structure provides an explicit low-order interaction bias for data efficiency and interpretability, while the rational parameterization significantly improves extrapolation. Across controlled function benchmarks and vision classification tasks (e.g., CIFAR-10) under matched parameter and compute budgets, RAN matches or surpasses parameter-matched MLPs and learnable-activation baselines, with better stability and throughput. Code is available at https://github.com/jushengzhang/Rational-ANOVA-Networks.git.

Clifford Kolmogorov-Arnold Networks

Authors: Matthias Wolff, Francesco Alesiani, Christof Duhme, Xiaoyi Jiang

Abstract: We introduce Clifford Kolmogorov-Arnold Network (ClKAN), a flexible and efficient architecture for function approximation in arbitrary Clifford algebra spaces. We propose the use of Randomized Quasi Monte Carlo grid generation as a solution to the exponential scaling associated with higher dimensional algebras. Our ClKAN also introduces new batch normalization strategies to deal with variable domain input. ClKAN finds application in scientific discovery and engineering, and is validated in synthetic and physics inspired tasks.

MGP-KAD: Multimodal Geometric Priors and Kolmogorov-Arnold Decoder for Single-View 3D Reconstruction in Complex Scenes

Authors: Luoxi Zhang, Chun Xie, Itaru Kitahara

Abstract: Single-view 3D reconstruction in complex real-world scenes is challenging due to noise, object diversity, and limited dataset availability. To address these challenges, we propose MGP-KAD, a novel multimodal feature fusion framework that integrates RGB and geometric prior to enhance reconstruction accuracy. The geometric prior is generated by sampling and clustering ground-truth object data, producing class-level features that dynamically adjust during training to improve geometric understanding. Additionally, we introduce a hybrid decoder based on Kolmogorov-Arnold Networks (KAN) to overcome the limitations of traditional linear decoders in processing complex multimodal inputs. Extensive experiments on the Pix3D dataset demonstrate that MGP-KAD achieves state-of-the-art (SOTA) performance, significantly improving geometric integrity, smoothness, and detail preservation. Our work provides a robust and effective solution for advancing single-view 3D reconstruction in complex scenes.

Optimal Abstractions for Verifying Properties of Kolmogorov-Arnold Networks (KANs)

Authors: Noah Schwartz, Chandra Kanth Nagesh, Sriram Sankaranarayanan, Ramneet Kaur, Tuhin Sahai, Susmit Jha

Abstract: We present a novel approach for verifying properties of Kolmogorov-Arnold Networks (KANs), a class of neural networks characterized by nonlinear, univariate activation functions typically implemented as piecewise polynomial splines or Gaussian processes. Our method creates mathematical ``abstractions’’ by replacing each KAN unit with a piecewise affine (PWA) function, providing both local and global error estimates between the original network and its approximation. These abstractions enable property verification by encoding the problem as a Mixed Integer Linear Program (MILP), determining whether outputs satisfy specified properties when inputs belong to a given set. A critical challenge lies in balancing the number of pieces in the PWA approximation: too many pieces add binary variables that make verification computationally intractable, while too few pieces create excessive error margins that yield uninformative bounds. Our key contribution is a systematic framework that exploits KAN structure to find optimal abstractions. By combining dynamic programming at the unit level with a knapsack optimization across the network, we minimize the total number of pieces while guaranteeing specified error bounds. This approach determines the optimal approximation strategy for each unit while maintaining overall accuracy requirements. Empirical evaluation across multiple KAN benchmarks demonstrates that the upfront analysis costs of our method are justified by superior verification results.

Learning to Anchor Visual Odometry: KAN-Based Pose Regression for Planetary Landing

Authors: Xubo Luo, Zhaojin Li, Xue Wan, Wei Zhang, Leizheng Shu

Abstract: Accurate and real-time 6-DoF localization is mission-critical for autonomous lunar landing, yet existing approaches remain limited: visual odometry (VO) drifts unboundedly, while map-based absolute localization fails in texture-sparse or low-light terrain. We introduce KANLoc, a monocular localization framework that tightly couples VO with a lightweight but robust absolute pose regressor. At its core is a Kolmogorov-Arnold Network (KAN) that learns the complex mapping from image features to map coordinates, producing sparse but highly reliable global pose anchors. These anchors are fused into a bundle adjustment framework, effectively canceling drift while retaining local motion precision. KANLoc delivers three key advances: (i) a KAN-based pose regressor that achieves high accuracy with remarkable parameter efficiency, (ii) a hybrid VO-absolute localization scheme that yields globally consistent real-time trajectories (>=15 FPS), and (iii) a tailored data augmentation strategy that improves robustness to sensor occlusion. On both realistic synthetic and real lunar landing datasets, KANLoc reduces average translation and rotation error by 32% and 45%, respectively, with per-trajectory gains of up to 45%/48%, outperforming strong baselines.

Physical Analog Kolmogorov-Arnold Networks based on Reconfigurable Nonlinear-Processing Units

Authors: Manuel Escudero, Mohamadreza Zolfagharinejad, Sjoerd van den Belt, Nikolaos Alachiotis, Wilfred G. van der Wiel

Abstract: Kolmogorov-Arnold Networks (KANs) shift neural computation from linear layers to learnable nonlinear edge functions, but implementing these nonlinearities efficiently in hardware remains an open challenge. Here we introduce a physical analog KAN architecture in which edge functions are realized in materia using reconfigurable nonlinear-processing units (RNPUs): multi-terminal nanoscale silicon devices whose input-output characteristics are tuned via control voltages. By combining multiple RNPUs into an edge processor and assembling these blocks into a reconfigurable analog KAN (aKAN) architecture with integrated mixed-signal interfacing, we establish a realistic system-level hardware implementation that enables compact KAN-style regression and classification with programmable nonlinear transformations. Using experimentally calibrated RNPU models and hardware measurements, we demonstrate accurate function approximation across increasing task complexity while requiring fewer or comparable trainable parameters than multilayer perceptrons (MLPs). System-level estimates indicate an energy per inference of $\sim$250 pJ and an end-to-end inference latency of $\sim$600 ns for a representative workload, corresponding to a $\sim$10$^{2}$-10$^{3}\times$ reduction in energy accompanied by a $\sim$10$\times$ reduction in area compared to a digital fixed-point MLP at similar approximation error. These results establish RNPUs as scalable, hardware-native nonlinear computing primitives and identify analog KAN architectures as a realistic silicon-based pathway toward energy-, latency-, and footprint-efficient analog neural-network hardware, particularly for edge inference.

Spectral Gating Networks

Authors: Jusheng Zhang, Yijia Fan, Kaitong Cai, Jing Yang, Yongsen Zheng, Kwok-Yan Lam, Liang Lin, Keze Wang

Abstract: Gating mechanisms are ubiquitous, yet a complementary question in feed-forward networks remains under-explored: how to introduce frequency-rich expressivity without sacrificing stability and scalability? This tension is exposed by spline-based Kolmogorov-Arnold Network (KAN) parameterizations, where grid refinement can induce parameter growth and brittle optimization in high dimensions. To propose a stability-preserving way to inject spectral capacity into existing MLP/FFN layers under fixed parameter and training budgets, we introduce Spectral Gating Networks (SGN), a drop-in spectral reparameterization. SGN augments a standard activation pathway with a compact spectral pathway and learnable gates that allow the model to start from a stable base behavior and progressively allocate capacity to spectral features during training. The spectral pathway is instantiated with trainable Random Fourier Features (learned frequencies and phases), replacing grid-based splines and removing resolution dependence. A hybrid GELU-Fourier formulation further improves optimization robustness while enhancing high-frequency fidelity. Across vision, NLP, audio, and PDE benchmarks, SGN consistently improves accuracy-efficiency trade-offs under comparable computational budgets, achieving 93.15% accuracy on CIFAR-10 and up to 11.7x faster inference than spline-based KAN variants. Code and trained models will be released.

A hybrid Kolmogorov-Arnold network for medical image segmentation

Authors: Deep Bhattacharyya, Ali Ayub, A. Ben Hamza

Abstract: Medical image segmentation plays a vital role in diagnosis and treatment planning, but remains challenging due to the inherent complexity and variability of medical images, especially in capturing non-linear relationships within the data. We propose U-KABS, a novel hybrid framework that integrates the expressive power of Kolmogorov-Arnold Networks (KANs) with a U-shaped encoder-decoder architecture to enhance segmentation performance. The U-KABS model combines the convolutional and squeeze-and-excitation stage, which enhances channel-wise feature representations, and the KAN Bernstein Spline (KABS) stage, which employs learnable activation functions based on Bernstein polynomials and B-splines. This hybrid design leverages the global smoothness of Bernstein polynomials and the local adaptability of B-splines, enabling the model to effectively capture both broad contextual trends and fine-grained patterns critical for delineating complex structures in medical images. Skip connections between encoder and decoder layers support effective multi-scale feature fusion and preserve spatial details. Evaluated across diverse medical imaging benchmark datasets, U-KABS demonstrates superior performance compared to strong baselines, particularly in segmenting complex anatomical structures.

Empirical Stability Analysis of Kolmogorov-Arnold Networks in Hard-Constrained Recurrent Physics-Informed Discovery

Authors: Enzo Nicolas Spotorno, Josafat Leal Filho, Antonio Augusto Medeiros Frohlich

Abstract: We investigate the integration of Kolmogorov-Arnold Networks (KANs) into hard-constrained recurrent physics-informed architectures (HRPINN) to evaluate the fidelity of learned residual manifolds in oscillatory systems. Motivated by the Kolmogorov-Arnold representation theorem and preliminary gray-box results, we hypothesized that KANs would enable efficient recovery of unknown terms compared to MLPs. Through initial sensitivity analysis on configuration sensitivity, parameter scale, and training paradigm, we found that while small KANs are competitive on univariate polynomial residuals (Duffing), they exhibit severe hyperparameter fragility, instability in deeper configurations, and consistent failure on multiplicative terms (Van der Pol), generally outperformed by standard MLPs. These empirical challenges highlight limitations of the additive inductive bias in the original KAN formulation for state coupling and provide preliminary empirical evidence of inductive bias limitations for future hybrid modeling.

GAC-KAN: An Ultra-Lightweight GNSS Interference Classifier for GenAI-Powered Consumer Edge Devices

Authors: Zhihan Zeng, Kaihe Wang, Zhongpei Zhang, Yue Xiu

Abstract: The integration of Generative AI (GenAI) into Consumer Electronics (CE)–from AI-powered assistants in wearables to generative planning in autonomous Uncrewed Aerial Vehicles (UAVs)–has revolutionized user experiences. However, these GenAI applications impose immense computational burdens on edge hardware, leaving strictly limited resources for fundamental security tasks like Global Navigation Satellite System (GNSS) signal protection. Furthermore, training robust classifiers for such devices is hindered by the scarcity of real-world interference data. To address the dual challenges of data scarcity and the extreme efficiency required by the GenAI era, this paper proposes a novel framework named GAC-KAN. First, we adopt a physics-guided simulation approach to synthesize a large-scale, high-fidelity jamming dataset, mitigating the data bottleneck. Second, to reconcile high accuracy with the stringent resource constraints of GenAI-native chips, we design a Multi-Scale Ghost-ACB-Coordinate (MS-GAC) backbone. This backbone combines Asymmetric Convolution Blocks (ACB) and Ghost modules to extract rich spectral-temporal features with minimal redundancy. Replacing the traditional Multi-Layer Perceptron (MLP) decision head, we introduce a Kolmogorov-Arnold Network (KAN), which employs learnable spline activation functions to achieve superior non-linear mapping capabilities with significantly fewer parameters. Experimental results demonstrate that GAC-KAN achieves an overall accuracy of 98.0\%, outperforming state-of-the-art baselines. Significantly, the model contains only 0.13 million parameter–approximately 660 times fewer than Vision Transformer (ViT) baselines. This extreme lightweight characteristic makes GAC-KAN an ideal “always-on” security companion, ensuring GNSS reliability without contending for the computational resources required by primary GenAI tasks.

Time-TK: A Multi-Offset Temporal Interaction Framework Combining Transformer and Kolmogorov-Arnold Networks for Time Series Forecasting

Authors: Fan Zhang, Shiming Fan, Hua Wang

Abstract: Time series forecasting is crucial for the World Wide Web and represents a core technical challenge in ensuring the stable and efficient operation of modern web services, such as intelligent transportation and website throughput. However, we have found that existing methods typically employ a strategy of embedding each time step as an independent token. This paradigm introduces a fundamental information bottleneck when processing long sequences, the root cause of which is that independent token embedding destroys a crucial structure within the sequence - what we term as multi-offset temporal correlation. This refers to the fine-grained dependencies embedded within the sequence that span across different time steps, which is especially prevalent in regular Web data. To fundamentally address this issue, we propose a new perspective on time series embedding. We provide an upper bound on the approximate reconstruction performance of token embedding, which guides our design of a concise yet effective Multi-Offset Time Embedding method to mitigate the performance degradation caused by standard token embedding. Furthermore, our MOTE can be integrated into various existing models and serve as a universal building block. Based on this paradigm, we further design a novel forecasting architecture named Time-TK. This architecture first utilizes a Multi-Offset Interactive KAN to learn and represent specific temporal patterns among multiple offset sub-sequences. Subsequently, it employs an efficient Multi-Offset Temporal Interaction mechanism to effectively capture the complex dependencies between these sub-sequences, achieving global information integration. Extensive experiments on 14 real-world benchmark datasets, covering domains such as traffic flow and BTC/USDT throughput, demonstrate that Time-TK significantly outperforms all baseline models, achieving state-of-the-art forecasting accuracy.

KAN-FIF: Spline-Parameterized Lightweight Physics-based Tropical Cyclone Estimation on Meteorological Satellite

Authors: Jiakang Shen, Qinghui Chen, Runtong Wang, Chenrui Xu, Jinglin Zhang, Cong Bai, Feng Zhang

Abstract: Tropical cyclones (TC) are among the most destructive natural disasters, causing catastrophic damage to coastal regions through extreme winds, heavy rainfall, and storm surges. Timely monitoring of tropical cyclones is crucial for reducing loss of life and property, yet it is hindered by the computational inefficiency and high parameter counts of existing methods on resource-constrained edge devices. Current physics-guided models suffer from linear feature interactions that fail to capture high-order polynomial relationships between TC attributes, leading to inflated model sizes and hardware incompatibility. To overcome these challenges, this study introduces the Kolmogorov-Arnold Network-based Feature Interaction Framework (KAN-FIF), a lightweight multimodal architecture that integrates MLP and CNN layers with spline-parameterized KAN layers. For Maximum Sustained Wind (MSW) prediction, experiments demonstrate that the KAN-FIF framework achieves a $94.8\%$ reduction in parameters (0.99MB vs 19MB) and $68.7\%$ faster inference per sample (2.3ms vs 7.35ms) compared to baseline model Phy-CoCo, while maintaining superior accuracy with $32.5\%$ lower MAE. The offline deployment experiment of the FY-4 series meteorological satellite processor on the Qingyun-1000 development board achieved a 14.41ms per-sample inference latency with the KAN-FIF framework, demonstrating promising feasibility for operational TC monitoring and extending deployability to edge-device AI applications. The code is released at https://github.com/Jinglin-Zhang/KAN-FIF.

Realistic Face Reconstruction from Facial Embeddings via Diffusion Models

Authors: Dong Han, Yong Li, Joachim Denzler

Abstract: With the advancement of face recognition (FR) systems, privacy-preserving face recognition (PPFR) systems have gained popularity for their accurate recognition, enhanced facial privacy protection, and robustness to various attacks. However, there are limited studies to further verify privacy risks by reconstructing realistic high-resolution face images from embeddings of these systems, especially for PPFR. In this work, we propose the face embedding mapping (FEM), a general framework that explores Kolmogorov-Arnold Network (KAN) for conducting the embedding-to-face attack by leveraging pre-trained Identity-Preserving diffusion model against state-of-the-art (SOTA) FR and PPFR systems. Based on extensive experiments, we verify that reconstructed faces can be used for accessing other real-word FR systems. Besides, the proposed method shows the robustness in reconstructing faces from the partial and protected face embeddings. Moreover, FEM can be utilized as a tool for evaluating safety of FR and PPFR systems in terms of privacy leakage. All images used in this work are from public datasets.

A Unified Benchmark of Physics-Informed Neural Networks and Kolmogorov-Arnold Networks for Ordinary and Partial Differential Equations

Authors: Salvador K. Dzimah, Sonia Rubio Herranz, Fernando Carlos Lopez Hernandez, Antonio López Montes

Abstract: Physics-Informed Neural Networks (PINNs) have emerged as a powerful mesh-free framework for solving ordinary and partial differential equations by embedding the governing physical laws directly into the loss function. However, their classical formulation relies on multilayer perceptrons (MLPs), whose fixed activation functions and global approximation biases limit performance in problems with oscillatory behavior, multiscale dynamics, or sharp gradients. In parallel, Kolmogorov-Arnold Networks (KANs) have been introduced as a functionally adaptive architecture based on learnable univariate transformations along each edge, providing richer local approximations and improved expressivity. This work presents a systematic and controlled comparison between standard MLP-based PINNs and their KAN-based counterparts, Physics-Informed Kolmogorov-Arnold Networks (PIKANs), using identical physics-informed formulations and matched parameter budgets to isolate the architectural effect. Both models are evaluated across a representative collection of ODEs and PDEs, including cases with known analytical solutions that allow direct assessment of gradient reconstruction accuracy. The results show that PIKANs consistently achieve more accurate solutions, converge in fewer iterations, and yield superior gradient estimates, highlighting their advantage for physics-informed learning. These findings underline the potential of KAN-based architectures as a next-generation approach for scientific machine learning and provide rigorous evidence to guide model selection in differential equation solving.

Predicting Invoice Dilution in Supply Chain Finance with Leakage Free Two Stage XGBoost, KAN (Kolmogorov Arnold Networks), and Ensemble Models

Authors: Pavel Koptev, Vishnu Kumar, Konstantin Malkov, George Shapiro, Yury Vikhanov

Abstract: Invoice or payment dilution is the gap between the approved invoice amount and the actual collection is a significant source of non credit risk and margin loss in supply chain finance. Traditionally, this risk is managed through the buyer’s irrevocable payment undertaking (IPU), which commits to full payment without deductions. However, IPUs can hinder supply chain finance adoption, particularly among sub-invested grade buyers. A newer, data-driven methods use real-time dynamic credit limits, projecting dilution for each buyer-supplier pair in real-time. This paper introduces an AI, machine learning framework and evaluates how that can supplement a deterministic algorithm to predict invoice dilution using extensive production dataset across nine key transaction fields.

A Graph Meta-Network for Learning on Kolmogorov-Arnold Networks

Authors: Guy Bar-Shalom, Ami Tavory, Itay Evron, Maya Bechler-Speicher, Ido Guy, Haggai Maron

Abstract: Weight-space models learn directly from the parameters of neural networks, enabling tasks such as predicting their accuracy on new datasets. Naive methods – like applying MLPs to flattened parameters – perform poorly, making the design of better weight-space architectures a central challenge. While prior work leveraged permutation symmetries in standard networks to guide such designs, no analogous analysis or tailored architecture yet exists for Kolmogorov-Arnold Networks (KANs). In this work, we show that KANs share the same permutation symmetries as MLPs, and propose the KAN-graph, a graph representation of their computation. Building on this, we develop WS-KAN, the first weight-space architecture that learns on KANs, which naturally accounts for their symmetry. We analyze WS-KAN’s expressive power, showing it can replicate an input KAN’s forward pass - a standard approach for assessing expressiveness in weight-space architectures. We construct a comprehensive ``zoo’’ of trained KANs spanning diverse tasks, which we use as benchmarks to empirically evaluate WS-KAN. Across all tasks, WS-KAN consistently outperforms structure-agnostic baselines, often by a substantial margin. Our code is available at https://github.com/BarSGuy/KAN-Graph-Metanetwork.

FEKAN: Feature-Enriched Kolmogorov-Arnold Networks

Authors: Sidharth S. Menon, Ameya D. Jagtap

Abstract: Kolmogorov-Arnold Networks (KANs) have recently emerged as a compelling alternative to multilayer perceptrons, offering enhanced interpretability via functional decomposition. However, existing KAN architectures, including spline-, wavelet-, radial-basis variants, etc., suffer from high computational cost and slow convergence, limiting scalability and practical applicability. Here, we introduce Feature-Enriched Kolmogorov-Arnold Networks (FEKAN), a simple yet effective extension that preserves all the advantages of KAN while improving computational efficiency and predictive accuracy through feature enrichment, without increasing the number of trainable parameters. By incorporating these additional features, FEKAN accelerates convergence, increases representation capacity, and substantially mitigates the computational overhead characteristic of state-of-the-art KAN architectures. We investigate FEKAN across a comprehensive set of benchmarks, including function-approximation tasks, physics-informed formulations for diverse partial differential equations (PDEs), and neural operator settings that map between input and output function spaces. For function approximation, we systematically compare FEKAN against a broad family of KAN variants, FastKAN, WavKAN, ReLUKAN, HRKAN, ChebyshevKAN, RBFKAN, and the original SplineKAN. Across all tasks, FEKAN demonstrates substantially faster convergence and consistently higher approximation accuracy than the underlying baseline architectures. We also establish the theoretical foundations for FEKAN, showing its superior representation capacity compared to KAN, which contributes to improved accuracy and efficiency.

Inelastic Constitutive Kolmogorov-Arnold Networks: A generalized framework for automated discovery of interpretable inelastic material models

Authors: Chenyi Ji, Kian P. Abdolazizi, Hagen Holthusen, Christian J. Cyron, Kevin Linka

Abstract: A key problem of solid mechanics is the identification of the constitutive law of a material, that is, the relation between strain and stress. Machine learning has lead to considerable advances in this field lately. Here we introduce inelastic Constitutive Kolmogorov-Arnold Networks (iCKANs). This novel artificial neural network architecture can discover in an automated manner symbolic constitutive laws describing both the elastic and inelastic behavior of materials. That is, it can translate data from material testing into corresponding elastic and inelastic potential functions in closed mathematical form. We demonstrate the advantages of iCKANs using both synthetic data and experimental data of the viscoelastic polymer materials VHB 4910 and VHB 4905. The results demonstrate that iCKANs accurately capture complex viscoelastic behavior while preserving physical interpretability. It is a particular strength of iCKANs that they can process not only mechanical data but also arbitrary additional information available about a material (e.g., about temperature-dependent behavior). This makes iCKANs a powerful tool to discover in the future also how specific processing or service conditions affect the properties of materials.

Weak-Form Evolutionary Kolmogorov-Arnold Networks for Solving Partial Differential Equations

Authors: Bongseok Kim, Jiahao Zhang, Guang Lin

Abstract: Partial differential equations (PDEs) form a central component of scientific computing. Among recent advances in deep learning, evolutionary neural networks have been developed to successively capture the temporal dynamics of time-dependent PDEs via parameter evolution. The parameter updates are obtained by solving a linear system derived from the governing equation residuals at each time step. However, strong-form evolutionary approaches can yield ill-conditioned linear systems due to pointwise residual discretization, and their computational cost scales unfavorably with the number of training samples. To address these limitations, we propose a weak-form evolutionary Kolmogorov-Arnold Network (KAN) for the scalable and accurate prediction of PDE solutions. We decouple the linear system size from the number of training samples through the weak formulation, leading to improved scalability compared to strong-form approaches. We also rigorously enforce boundary conditions by constructing the trial space with boundary-constrained KANs to satisfy Dirichlet and periodic conditions, and by incorporating derivative boundary conditions directly into the weak formulation for Neumann conditions. In conclusion, the proposed weak-form evolutionary KAN framework provides a stable and scalable approach for PDEs and contributes to scientific machine learning with potential relevance to future engineering applications.

Spectral bias in physics-informed and operator learning: Analysis and mitigation guidelines

Authors: Siavash Khodakarami, Vivek Oommen, Nazanin Ahmadi Daryakenari, Maxim Beekenkamp, George Em Karniadakis

Abstract: Solving partial differential equations (PDEs) by neural networks as well as Kolmogorov-Arnold Networks (KANs), including physics-informed neural networks (PINNs), physics-informed KANs (PIKANs), and neural operators, are known to exhibit spectral bias, whereby low-frequency components of the solution are learned significantly faster than high-frequency modes. While spectral bias is often treated as an intrinsic representational limitation of neural architectures, its interaction with optimization dynamics and physics-based loss formulations remains poorly understood. In this work, we provide a systematic investigation of spectral bias in physics-informed and operator learning frameworks, with emphasis on the coupled roles of network architecture, activation functions, loss design, and optimization strategy. We quantify spectral bias through frequency-resolved error metrics, Barron-norm diagnostics, and higher-order statistical moments, enabling a unified analysis across elliptic, hyperbolic, and dispersive PDEs. Through diverse benchmark problems, including the Korteweg-de Vries, wave and steady-state diffusion-reaction equations, turbulent flow reconstruction, and earthquake dynamics, we demonstrate that spectral bias is not simply representational but fundamentally dynamical. In particular, second-order optimization methods substantially alter the spectral learning order, enabling earlier and more accurate recovery of high-frequency modes for all PDE types. For neural operators, we further show that spectral bias is dependent on the neural operator architecture and can also be effectively mitigated through spectral-aware loss formulations without increasing the inference cost.

KANDy: Kolmogorov-Arnold Networks and Dynamical System Discovery

Authors: Kevin Slote, Jeremie Fish, Erik Bollt

Abstract: We introduce the Kolmogorov-Arnold Network for Dynamics (KANDy) as a zero-depth, wide neural architecture capable of discovering governing equations in chaotic and complex dynamical systems. Building on the foundation of Kolmogorov-Arnold Networks (KANs), KANDy explicitly learns governing equations by replacing sparse regression with a KAN. The synthesis of KANs and sparse regression addresses the limitations of equation discovery for KANs applied to dynamical systems and overcomes cases where sparse regression is hindered by sparsity constraints. Additionally, we show that our model, applied to the Hopf Fibration, recovers topological structure, thereby improving coherence with attractor properties. We apply our model to discrete and continuous dynamical systems, as well as to chaotic partial differential equations (PDEs). These results position KANDy as an interpretable and effective alternative for data-driven modeling of nonlinear dynamical systems.

LESA: Learnable Stage-Aware Predictors for Diffusion Model Acceleration

Authors: Peiliang Cai, Jiacheng Liu, Haowen Xu, Xinyu Wang, Chang Zou, Linfeng Zhang

Abstract: Diffusion models have achieved remarkable success in image and video generation tasks. However, the high computational demands of Diffusion Transformers (DiTs) pose a significant challenge to their practical deployment. While feature caching is a promising acceleration strategy, existing methods based on simple reusing or training-free forecasting struggle to adapt to the complex, stage-dependent dynamics of the diffusion process, often resulting in quality degradation and failing to maintain consistency with the standard denoising process. To address this, we propose a LEarnable Stage-Aware (LESA) predictor framework based on two-stage training. Our approach leverages a Kolmogorov-Arnold Network (KAN) to accurately learn temporal feature mappings from data. We further introduce a multi-stage, multi-expert architecture that assigns specialized predictors to different noise-level stages, enabling more precise and robust feature forecasting. Extensive experiments show our method achieves significant acceleration while maintaining high-fidelity generation. Experiments demonstrate 5.00x acceleration on FLUX.1-dev with minimal quality degradation (1.0% drop), 6.25x speedup on Qwen-Image with a 20.2% quality improvement over the previous SOTA (TaylorSeer), and 5.00x acceleration on HunyuanVideo with a 24.7% PSNR improvement over TaylorSeer. State-of-the-art performance on both text-to-image and text-to-video synthesis validates the effectiveness and generalization capability of our training-based framework across different models. Our code is included in the supplementary materials and will be released on GitHub.

Physics-Informed Machine Learning for Vessel Shaft Power and Fuel Consumption Prediction: Interpretable KAN-based Approach

Authors: Hamza Haruna Mohammed, Dusica Marijan, Arnbjørn Maressa

Abstract: Accurate prediction of shaft rotational speed, shaft power, and fuel consumption is crucial for enhancing operational efficiency and sustainability in maritime transportation. Conventional physics-based models provide interpretability but struggle with real-world variability, while purely data-driven approaches achieve accuracy at the expense of physical plausibility. This paper introduces a Physics-Informed Kolmogorov-Arnold Network (PI-KAN), a hybrid method that integrates interpretable univariate feature transformations with a physics-informed loss function and a leakage-free chained prediction pipeline. Using operational and environmental data from five cargo vessels, PI-KAN consistently outperforms the traditional polynomial method and neural network baselines. The model achieves the lowest mean absolute error (MAE) and root mean squared error (RMSE), and the highest coefficient of determination (R^2) for shaft power and fuel consumption across all vessels, while maintaining physically consistent behavior. Interpretability analysis reveals rediscovery of domain-consistent dependencies, such as cubic-like speed-power relationships and cosine-like wave and wind effects. These results demonstrate that PI-KAN achieves both predictive accuracy and interpretability, offering a robust tool for vessel performance monitoring and decision support in operational settings.

KMLP: A Scalable Hybrid Architecture for Web-Scale Tabular Data Modeling

Authors: Mingming Zhang, Pengfei Shi, Zhiqing Xiao, Feng Zhao, Guandong Sun, Yulin Kang, Ruizhe Gao, Ningtao Wang, Xing Fu, Weiqiang Wang, Junbo Zhao

Abstract: Predictive modeling on web-scale tabular data with billions of instances and hundreds of heterogeneous numerical features faces significant scalability challenges. These features exhibit anisotropy, heavy-tailed distributions, and non-stationarity, creating bottlenecks for models like Gradient Boosting Decision Trees and requiring laborious manual feature engineering. We introduce KMLP, a hybrid deep architecture integrating a shallow Kolmogorov-Arnold Network (KAN) front-end with a Gated Multilayer Perceptron (gMLP) backbone. The KAN front-end uses learnable activation functions to automatically model complex non-linear transformations for each feature, while the gMLP backbone captures high-order interactions. Experiments on public benchmarks and an industrial dataset with billions of samples show KMLP achieves state-of-the-art performance, with advantages over baselines like GBDTs increasing at larger scales, validating KMLP as a scalable deep learning paradigm for large-scale web tabular data.

BiKA: Kolmogorov-Arnold-Network-inspired Ultra Lightweight Neural Network Hardware Accelerator

Authors: Yuhao Liu, Salim Ullah, Akash Kumar

Abstract: Lightweight neural network accelerators are essential for edge devices with limited resources and power constraints. While quantization and binarization can efficiently reduce hardware cost, they still rely on the conventional Artificial Neural Network (ANN) computation pattern. The recently proposed Kolmogorov-Arnold Network (KAN) presents a novel network paradigm built on learnable nonlinear functions. However, it is computationally expensive for hardware deployment. Inspired by KAN, we propose BiKA, a multiply-free architecture that replaces nonlinear functions with binary, learnable thresholds, introducing an extremely lightweight computational pattern that requires only comparators and accumulators. Our FPGA prototype on Ultra96-V2 shows that BiKA reduces hardware resource usage by 27.73% and 51.54% compared with binarized and quantized neural network systolic array accelerators, while maintaining competitive accuracy. BiKA provides a promising direction for hardware-friendly neural network design on edge devices.

March

TokenCom: Vision-Language Model for Multimodal and Multitask Token Communications

Authors: Feibo Jiang, Siwei Tu, Li Dong, Xiaolong Li, Kezhi Wang, Cunhua Pan, Zhu Han, Jiangzhou Wang

Abstract: Visual-Language Models (VLMs), with their strong capabilities in image and text understanding, offer a solid foundation for intelligent communications. However, their effectiveness is constrained by limited token granularity, overlong visual token sequences, and inadequate cross-modal alignment. To overcome these challenges, we propose TaiChi, a novel VLM framework designed for token communications. TaiChi adopts a dual-visual tokenizer architecture that processes both high- and low-resolution images to collaboratively capture pixel-level details and global conceptual features. A Bilateral Attention Network (BAN) is introduced to intelligently fuse multi-scale visual tokens, thereby enhancing visual understanding and producing compact visual tokens. In addition, a Kolmogorov Arnold Network (KAN)-based modality projector with learnable activation functions is employed to achieve precise nonlinear alignment from visual features to the text semantic space, thus minimizing information loss. Finally, TaiChi is integrated into a multimodal and multitask token communication system equipped with a joint VLM-channel coding scheme. Experimental results validate the superior performance of TaiChi, as well as the feasibility and effectiveness of the TaiChi-driven token communication system.

VIKIN: A Reconfigurable Accelerator for KANs and MLPs with Two-Stage Sparsity Support

Authors: Wenhui Ou, Zhuoyu Wu, Yipu Zhang, Zheng Wang, C. Patrick Yue

Abstract: Recently, multi-layer perceptrons (MLPs) widely used in modern AI applications suffer from limited real-time performance due to intensive memory access overhead. Kolmogorov–Arnold Networks (KANs) have attracted increasing attention as an alternative architecture with similar structures to MLPs but improved parameter efficiency. However, the lack of dedicated hardware support limits the practical performance benefits of KANs. Moreover, since many edge workloads still rely heavily on MLPs, accelerators designed exclusively for KANs become inefficient and impractical. In this work, we present VIKIN, a reconfigurable accelerator that efficiently supports both KAN and MLP inference using unified hardware. VIKIN introduces a pipeline execution mode and two-stage sparsity support for efficient KAN processing, while enabling parallel-mode acceleration to improve MLP throughput under the same sparsity framework. Experiments on real-world datasets demonstrate that replacing MLPs with KANs on VIKIN achieves $1.28\times$ acceleration with $19.58\%$ reduced accuracy loss. For a higher-accuracy KAN model requiring $3.29\times$ more operations, VIKIN incurs only $1.24\times$ latency overhead compared with the baseline KAN model. In addition, VIKIN achieves $1.25\times$ speedup and $4.87\times$ higher energy efficiency than a representative edge GPU when executing KAN workloads.

Merged amplitude encoding for Chebyshev quantum Kolmogorov–Arnold networks: trading qubits for circuit executions

Author: Hikaru Wakaura

Abstract: Quantum Kolmogorov–Arnold networks based on Chebyshev polynomials (CCQKAN) evaluate each edge activation function as a quantum inner product, creating a trade-off between qubit count and the number of circuit executions per forward pass. We introduce merged amplitude encoding, a technique that packs the element-wise products of all $n$ input-edge vectors for a given output node into a single amplitude state, reducing circuit executions by a factor of $n$ at a cost of only 1–2 additional qubits relative to the sequential baseline. The merged and original circuits compute the same mathematical quantity exactly; the open question is whether they remain equally trainable within a gradient-based optimization loop. We address this question through numerical experiments on 10 network configurations under ideal, finite-shot, and noisy simulation conditions, comparing original, parameter-transferred, and independently initialized merged circuits over 16 random seeds. Wilcoxon signed-rank tests show no significant difference between the independently initialized merged circuit and the original ($p > 0.05$ in 28 of 30 comparisons), while parameter transfer yields significantly lower loss under ideal conditions ($p < 0.001$ in 9 of 10 configurations). On 10-class digit classification with the $8\times8$ MNIST dataset using a one-vs-all strategy, original and merged circuits achieve comparable test accuracies of 53–78\% with no significant difference in any configuration. These results provide empirical evidence that merged amplitude encoding preserves trainability under the simulation conditions tested.

DKD-KAN: A Lightweight knowledge-distilled KAN intrusion detection framework, based on MLP and KAN

Author: Mohammad Alikhani

Abstract: Cyber-security systems often operate in resource-constrained environments, such as edge environments and real-time monitoring systems, where model size and inference time are crucial. A light-weight intrusion detection framework is proposed that utilizes the Kolmogorov-Arnold Network (KAN) to capture complex features in the data, with the efficiency of decoupled knowledge distillation (DKD) training approach. A high-capacity KAN network is first trained to detect attacks performed on the test bed. This model then serves as a teacher to guide a much smaller multilayer perceptron (MLP) student model via DKD. The resulting DKD-MLP model contains only 2,522 and 1,622 parameters for WADI and SWaT datasets, which are significantly smaller than the number of parameters of the KAN teacher model. This is highly appropriate for deployment in resource-constrained devices with limited computational resources. Despite its low size, the student model maintains a high performance. Our approach demonstrate the practicality of using KAN as a knowledge-rich teacher to train much smaller student models, without considerable drop in accuracy in intrusion detection frameworks. We have validated our approach on two publicly available datasets. We report F1-score improvements of 4.18% on WADI and 3.07% on SWaT when using the DKD-MLP model, compared to the bare student model. The implementation of this paper is available on our GitHub repository.

Multilevel Training for Kolmogorov Arnold Networks

Authors: Ben S. Southworth, Jonas A. Actor, Graham Harper, Eric C. Cyr

Abstract: Algorithmic speedup of training common neural architectures is made difficult by the lack of structure guaranteed by the function compositions inherent to such networks. In contrast to multilayer perceptrons (MLPs), Kolmogorov-Arnold networks (KANs) provide more structure by expanding learned activations in a specified basis. This paper exploits this structure to develop practical algorithms and theoretical insights, yielding training speedup via multilevel training for KANs. To do so, we first establish an equivalence between KANs with spline basis functions and multichannel MLPs with power ReLU activations through a linear change of basis. We then analyze how this change of basis affects the geometry of gradient-based optimization with respect to spline knots. The KANs change-of-basis motivates a multilevel training approach, where we train a sequence of KANs naturally defined through a uniform refinement of spline knots with analytic geometric interpolation operators between models. The interpolation scheme enables a ``properly nested hierarchy’’ of architectures, ensuring that interpolation to a fine model preserves the progress made on coarse models, while the compact support of spline basis functions ensures complementary optimization on subsequent levels. Numerical experiments demonstrate that our multilevel training approach can achieve orders of magnitude improvement in accuracy over conventional methods to train comparable KANs or MLPs, particularly for physics informed neural networks. Finally, this work demonstrates how principled design of neural networks can lead to exploitable structure, and in this case, multilevel algorithms that can dramatically improve training performance.

DualFlexKAN: Dual-stage Kolmogorov-Arnold Networks with Independent Function Control

Authors: Andrés Ortiz, Nicolás J. Gallego-Molina, Carmen Jiménez-Mesa, Juan M. Górriz, Javier Ramírez

Abstract: Multi-Layer Perceptrons (MLPs) rely on pre-defined, fixed activation functions, imposing a static inductive bias that forces the network to approximate complex topologies solely through increased depth and width. Kolmogorov-Arnold Networks (KANs) address this limitation through edge-centric learnable functions, yet their formulation suffers from quadratic parameter scaling and architectural rigidity that hinders the effective integration of standard regularization techniques. This paper introduces the DualFlexKAN (DFKAN), a flexible architecture featuring a dual-stage mechanism that independently controls pre-linear input transformations and post-linear output activations. This decoupling enables hybrid networks that optimize the trade-off between expressiveness and computational cost. Unlike standard formulations, DFKAN supports diverse basis function families, including orthogonal polynomials, B-splines, and radial basis functions, integrated with configurable regularization strategies that stabilize training dynamics. Comprehensive evaluations across regression benchmarks, physics-informed tasks, and function approximation demonstrate that DFKAN outperforms both MLPs and conventional KANs in accuracy, convergence speed, and gradient fidelity. The proposed hybrid configurations achieve superior performance with one to two orders of magnitude fewer parameters than standard KANs, effectively mitigating the parameter explosion problem while preserving KAN-style expressiveness. DFKAN provides a principled, scalable framework for incorporating adaptive non-linearities, proving particularly advantageous for data-efficient learning and interpretable function discovery in scientific applications.

Towards Faithful Multimodal Concept Bottleneck Models

Authors: Pierre Moreau, Emeline Pineau Ferrand, Yann Choho, Benjamin Wong, Annabelle Blangero, Milan Bhan

Abstract: Concept Bottleneck Models (CBMs) are interpretable models that route predictions through a layer of human-interpretable concepts. While widely studied in vision and, more recently, in NLP, CBMs remain largely unexplored in multimodal settings. For their explanations to be faithful, CBMs must satisfy two conditions: concepts must be properly detected, and concept representations must encode only their intended semantics, without smuggling extraneous task-relevant or inter-concept information into final predictions, a phenomenon known as leakage. Existing approaches treat concept detection and leakage mitigation as separate problems, and typically improve one at the expense of predictive accuracy. In this work, we introduce f-CBM, a faithful multimodal CBM framework built on a vision-language backbone that jointly targets both aspects through two complementary strategies: a differentiable leakage loss to mitigate leakage, and a Kolmogorov-Arnold Network prediction head that provides sufficient expressiveness to improve concept detection. Experiments demonstrate that f-CBM achieves the best trade-off between task accuracy, concept detection, and leakage reduction, while applying seamlessly to both image and text or text-only datasets, making it versatile across modalities.

PAKAN: Pixel Adaptive Kolmogorov-Arnold Network Modules for Pansharpening

Authors: Haoyu Zhang, Haojing Chen, Zhen Zhong, Liangjian Deng

Abstract: Pansharpening aims to fuse high-resolution spatial details from panchromatic images with the rich spectral information of multispectral images. Existing deep neural networks for this task typically rely on static activation functions, which limit their ability to dynamically model the complex, non-linear mappings required for optimal spatial-spectral fusion. While the recently introduced Kolmogorov-Arnold Network (KAN) utilizes learnable activation functions, traditional KANs lack dynamic adaptability during inference. To address this limitation, we propose a Pixel Adaptive Kolmogorov-Arnold Network framework. Starting from KAN, we design two adaptive variants: a 2D Adaptive KAN that generates spline summation weights across spatial dimensions and a 1D Adaptive KAN that generates them across spectral channels. These two components are then assembled into PAKAN 2to1 for feature fusion and PAKAN 1to1 for feature refinement. Extensive experiments demonstrate that our proposed modules significantly enhance network performance, proving the effectiveness and superiority of pixel-adaptive activation in pansharpening tasks.

Bridging Theory and Data: Correcting Nuclear Mass Models with Interpretable Machine Learning

Authors: Yanhua Lu, Tianshuai Shang, Pengxiang Du, Jian Li, Haozhao Liang

Abstract: Nuclear mass prediction is one of the core issues in nuclear physics research, yet it faces the challenge of small-sample datasets with high complexity. This study introduces the Kolmogorov-Arnold Network (KAN) into the refinement of nuclear mass models, proposing an efficient and interpretable solution. By constructing the KAN-WS4 hybrid model, the prediction accuracy is significantly improved (the root mean square error is reduced from 0.3 MeV to 0.16 MeV). Furthermore, leveraging the intrinsic interpretability of KAN, feature importance analysis reveals that the proton number is the most critical factor influencing residuals, indicating potential systematic biases in proton-related terms within existing theoretical models. The method’s generality is demonstrated across five mass models. This study shows that KAN provides a novel approach to small-sample, high-complexity scientific problems. Its interpretability facilitates the data-driven discovery of physical laws, promising broad applicability to key nuclear physics issues.

In-Context Symbolic Regression for Robustness-Improved Kolmogorov-Arnold Networks

Authors: Francesco Sovrano, Lidia Losavio, Giulia Vilone, Marc Langheinrich

Abstract: Symbolic regression aims to replace black-box predictors with concise analytical expressions that can be inspected and validated in scientific machine learning. Kolmogorov-Arnold Networks (KANs) are well suited to this goal because each connection between adjacent units (an “edge”) is parametrised by a learnable univariate function that can, in principle, be replaced by a symbolic operator. In practice, however, symbolic extraction is a bottleneck: the standard KAN-to-symbol approach fits operators to each learned edge function in isolation, making the discrete choice sensitive to initialisation and non-convex parameter fitting, and ignoring how local substitutions interact through the full network. We study in-context symbolic regression for operator extraction in KANs, and present two complementary instantiations. Greedy in-context Symbolic Regression (GSR) performs greedy, in-context selection by choosing edge replacements according to end-to-end loss improvement after brief fine-tuning. Gated Matching Pursuit (GMP) amortises this in-context selection by training a differentiable gated operator layer that places an operator library behind sparse gates on each edge; after convergence, gates are discretised (optionally followed by a short in-context greedy refinement pass). We quantify robustness via one-factor-at-a-time (OFAT) hyper-parameter sweeps and assess both predictive error and qualitative consistency of recovered formulas. Across several experiments, greedy in-context symbolic regression achieves up to 99.8% reduction in median OFAT test MSE.

A Kolmogorov-Arnold Surrogate Model for Chemical Equilibria: Application to Solid Solutions

Authors: Leonardo Boledi, Dirk Bosbach, Jenna Poonoosamy

Abstract: The computational cost of geochemical solvers is a challenging matter. For reactive transport simulations, where chemical calculations are performed up to billions of times, it is crucial to reduce the total computational time. Existing publications have explored various machine-learning approaches to determine the most effective data-driven surrogate model. In particular, multilayer perceptrons are widely employed due to their ability to recognize nonlinear relationships. In this work, we focus on the recent Kolmogorov-Arnold networks, where learnable spline-based functions replace classical fixed activation functions. This architecture has achieved higher accuracy with fewer trainable parameters and has become increasingly popular for solving partial differential equations. First, we train a surrogate model based on an existing cement system benchmark. Then, we move to an application case for the geological disposal of nuclear waste, i.e., the determination of radionuclide-bearing solids solubilities. To the best of our knowledge, this work is the first to investigate co-precipitation with radionuclide incorporation using data-driven surrogate models, considering increasing levels of thermodynamic complexity from simple mechanical mixtures to non-ideal solid solutions of binary (Ba,Ra)SO$_4$ and ternary (Sr,Ba,Ra)SO$_4$ systems. On the cement benchmark, we demonstrate that the Kolmogorov-Arnold architecture outperforms multilayer perceptrons in both absolute and relative error metrics, reducing them by 62% and 59%, respectively. On the binary and ternary radium solid solution models, Kolmogorov-Arnold networks maintain median prediction errors near $1\times10^{-3}$. This is the first step toward employing surrogate models to speed up reactive transport simulations and optimize the safety assessment of deep geological waste repositories.

HMAR: Hierarchical Modality-Aware Expert and Dynamic Routing Medical Image Retrieval Architecture

Author: Aojie Yuan

Abstract: Medical image retrieval (MIR) is a critical component of computer-aided diagnosis, yet existing systems suffer from three persistent limitations: uniform feature encoding that fails to account for the varying clinical importance of anatomical structures, ambiguous similarity metrics based on coarse classification labels, and an exclusive focus on global image similarity that cannot meet the clinical demand for fine-grained region-specific retrieval. We propose HMAR (Hierarchical Modality-Aware Expert and Dynamic Routing), an adaptive retrieval framework built on a Mixture-of-Experts (MoE) architecture. HMAR employs a dual-expert mechanism: Expert0 extracts global features for holistic similarity matching, while Expert1 learns position-invariant local representations for precise lesion-region retrieval. A two-stage contrastive learning strategy eliminates the need for expensive bounding-box annotations, and a sliding-window matching algorithm enables dense local comparison at inference time. Hash codes are generated via Kolmogorov-Arnold Network (KAN) layers for efficient Hamming-distance search. Experiments on the RadioImageNet-CT dataset (16 clinical patterns, 29,903 images) show that HMAR achieves mean Average Precision (mAP) of 0.711 and 0.724 for 64-bit and 128-bit hash codes, improving over the state-of-the-art ACIR method by 0.7% and 1.1%, respectively.

KANtize: Exploring Low-bit Quantization of Kolmogorov-Arnold Networks for Efficient Inference

Authors: Sohaib Errabii, Olivier Sentieys, Marcello Traiola

Abstract: Kolmogorov-Arnold Networks (KANs) have gained attention for their potential to outperform Multi-Layer Perceptrons (MLPs) in terms of parameter efficiency and interpretability. Unlike traditional MLPs, KANs use learnable non-linear activation functions, typically spline functions, expressed as linear combinations of basis splines (B-splines). B-spline coefficients serve as the model’s learnable parameters. However, evaluating these spline functions increases computational complexity during inference. Conventional quantization reduces this complexity by lowering the numerical precision of parameters and activations. However, the impact of quantization on KANs, and especially its effectiveness in reducing computational complexity, is largely unexplored, particularly for quantization levels below 8 bits. The study investigates the impact of low-bit quantization on KANs and its impact on computational complexity and hardware efficiency. Results show that B-splines can be quantized to 2-3 bits with negligible loss in accuracy, significantly reducing computational complexity. Hence, we investigate the potential of using low-bit quantized precomputed tables as a replacement for the recursive B-spline algorithm. This approach aims to further reduce the computational complexity of KANs and enhance hardware efficiency while maintaining accuracy. For example, ResKAN18 achieves a 50x reduction in BitOps without loss of accuracy using low-bit-quantized B-spline tables. Additionally, precomputed 8-bit lookup tables improve GPU inference speedup by up to 2.9x, while on FPGA-based systolic-array accelerators, reducing B-spline table precision from 8 to 3 bits cuts resource usage by 36%, increases clock frequency by 50%, and enhances speedup by 1.24x. On a 28nm FD-SOI ASIC, reducing the B-spline bit-width from 16 to 3 bits achieves 72% area reduction and 50% higher maximum frequency.

SINDy-KANs: Sparse identification of non-linear dynamics through Kolmogorov-Arnold networks

Authors: Amanda A. Howard, Nicholas Zolman, Bruno Jacob, Steven L. Brunton, Panos Stinis

Abstract: Kolmogorov-Arnold networks (KANs) have arisen as a potential way to enhance the interpretability of machine learning. However, solutions learned by KANs are not necessarily interpretable, in the sense of being sparse or parsimonious. Sparse identification of nonlinear dynamics (SINDy) is a complementary approach that allows for learning sparse equations for dynamical systems from data; however, learned equations are limited by the library. In this work, we present SINDy-KANs, which simultaneously train a KAN and a SINDy-like representation to increase interpretability of KAN representations with SINDy applied at the level of each activation function, while maintaining the function compositions possible through deep KANs. We apply our method to a number of symbolic regression tasks, including dynamical systems, to show accurate equation discovery across a range of systems.

Kolmogorov-Arnold causal generative models

Authors: Alejandro Almodóvar, Mar Elizo, Patricia A. Apellániz, Santiago Zazo, Juan Parras

Abstract: Causal generative models provide a principled framework for answering observational, interventional, and counterfactual queries from observational data. However, many deep causal models rely on highly expressive architectures with opaque mechanisms, limiting auditability in high-stakes domains. We propose KaCGM, a causal generative model for mixed-type tabular data where each structural equation is parameterized by a Kolmogorov–Arnold Network (KAN). This decomposition enables direct inspection of learned causal mechanisms, including symbolic approximations and visualization of parent–child relationships, while preserving query-agnostic generative semantics. We introduce a validation pipeline based on distributional matching and independence diagnostics of inferred exogenous variables, allowing assessment using observational data alone. Experiments on synthetic and semi-synthetic benchmarks show competitive performance against state-of-the-art methods. A real-world cardiovascular case study further demonstrates the extraction of simplified structural equations and interpretable causal effects. These results suggest that expressive causal generative modeling and functional transparency can be achieved jointly, supporting trustworthy deployment in tabular decision-making settings. Code: https://github.com/aalmodovares/kacgm

Many-body mobility edges in one dimension revealed by efficient and interpretable feature-based learning with Kolmogorov-Arnold Networks

Authors: Siqi Dai, Tian-Cheng Yi, Xingbo Wei, Yunbo Zhang

Abstract: We study the many-body localization (MBL) transition in interacting fermionic systems on disordered one-dimensional lattices using a physics-informed machine-learning framework. Instead of feeding full many-body wave functions into the model, we construct a compact feature representation based on four physically motivated observables: the inverse participation ratio, the Shannon entropy, the many-body hybridization parameter, and the mean level-spacing ratio. These quantities capture complementary aspects of localization, entanglement, and spectral correlations, and are used to train a Kolmogorov–Arnold Network (KAN) classifier on eigenstates deep in the weak and strong disorder regimes. The resulting KAN achieves a validation accuracy exceeding $99.9\%$, comparable to that of convolutional neural networks trained directly on high-dimensional wave-function data, while requiring substantially reduced input dimensionality and significantly shorter training time. Applying the trained classifier across the full energy spectrum yields energy-resolved phase diagrams that reveal a clear many-body mobility edge and provide a consistent estimate of the critical disorder strength. The approach is inherently extensible: additional physically relevant observables can be incorporated into the feature space in a systematic manner without altering the overall architecture. Our results demonstrate that feature-based learning with KAN provides an efficient, scalable, and interpretable methodology for identifying many-body localization transitions, offering a practical alternative to raw-data-based neural network approaches.

YOLOv10 with Kolmogorov-Arnold networks and vision-language foundation models for interpretable object detection and trustworthy multimodal AI in computer vision perception

Authors: Marios Impraimakis, Daniel Vazquez, Feiyu Zhou

Abstract: The interpretable object detection capabilities of a novel Kolmogorov-Arnold network framework are examined here. The approach refers to a key limitation in computer vision for autonomous vehicles perception, and beyond. These systems offer limited transparency regarding the reliability of their confidence scores in visually degraded or ambiguous scenes. To address this limitation, a Kolmogorov-Arnold network is employed as an interpretable post-hoc surrogate to model the trustworthiness of the You Only Look Once (Yolov10) detections using seven geometric and semantic features. The additive spline-based structure of the Kolmogorov-Arnold network enables direct visualisation of each feature’s influence. This produces smooth and transparent functional mappings that reveal when the model’s confidence is well supported and when it is unreliable. Experiments on both Common Objects in Context (COCO), and images from the University of Bath campus demonstrate that the framework accurately identifies low-trust predictions under blur, occlusion, or low texture. This provides actionable insights for filtering, review, or downstream risk mitigation. Furthermore, a bootstrapped language-image (BLIP) foundation model generates descriptive captions of each scene. This tool enables a lightweight multimodal interface without affecting the interpretability layer. The resulting system delivers interpretable object detection with trustworthy confidence estimates. It offers a powerful tool for transparent and practical perception component for autonomous and multimodal artificial intelligence applications.

Symbolic–KAN: Kolmogorov-Arnold Networks with Discrete Symbolic Structure for Interpretable Learning

Authors: Salah A Faroughi, Farinaz Mostajeran, Amirhossein Arzani, Shirko Faroughi

Abstract: Symbolic discovery of governing equations is a long-standing goal in scientific machine learning, yet a fundamental trade-off persists between interpretability and scalable learning. Classical symbolic regression methods yield explicit analytic expressions but rely on combinatorial search, whereas neural networks scale efficiently with data and dimensionality but produce opaque representations. In this work, we introduce Symbolic Kolmogorov-Arnold Networks (Symbolic-KANs), a neural architecture that bridges this gap by embedding discrete symbolic structure directly within a trainable deep network. Symbolic-KANs represent multivariate functions as compositions of learned univariate primitives applied to learned scalar projections, guided by a library of analytic primitives, hierarchical gating, and symbolic regularization that progressively sharpens continuous mixtures into one-hot selections. After gated training and discretization, each active unit selects a single primitive and projection direction, yielding compact closed-form expressions without post-hoc symbolic fitting. Symbolic-KANs further act as scalable primitive discovery mechanisms, identifying the most relevant analytic components that can subsequently inform candidate libraries for sparse equation-learning methods. We demonstrate that Symbolic-KAN reliably recovers correct primitive terms and governing structures in data-driven regression and inverse dynamical systems. Moreover, the framework extends to forward and inverse physics-informed learning of partial differential equations, producing accurate solutions directly from governing constraints while constructing compact symbolic representations whose selected primitives reflect the true analytical structure of the underlying equations. These results position Symbolic-KAN as a step toward scalable, interpretable, and mechanistically grounded learning of governing laws.

KANEL: Kolmogorov-Arnold Network Ensemble Learning Enables Early Hit Enrichment in High-Throughput Virtual Screening

Authors: Pavel Koptev, Nikita Krainov, Konstantin Malkov, Alexander Tropsha

Abstract: Machine learning models of chemical bioactivity are increasingly used for prioritizing a small number of compounds in virtual screening libraries for experimental follow-up. In these applications, assessing model accuracy by early hit enrichment such as Positive Predicted Value (PPV) calculated for top N hits (PPV@N) is more appropriate and actionable than traditional global metrics such as AUC. We present KANEL, an ensemble workflow that combines interpretable Kolmogorov-Arnold Networks (KANs) with XGBoost, random forest, and multilayer perceptron models trained on complementary molecular representations (LillyMol descriptors, RDKit-derived descriptors, and Morgan fingerprints).

Nonlinear Factor Decomposition via Kolmogorov-Arnold Networks: A Spectral Approach to Asset Return Analysis

Author: David Breazu

Abstract: KAN-PCA is an autoencoder that uses a KAN as encoder and a linear map as decoder. It generalizes classical PCA by replacing linear projections with learned B-spline functions on each edge. The motivation is to capture more variance than classical PCA, which becomes inefficient during market crises when the linear assumption breaks down and correlations between assets change dramatically. We prove that if the spline activations are forced to be linear, KAN-PCA yields exactly the same results as classical PCA, establishing PCA as a special case. Experiments on 20 S&P 500 stocks (2015-2024) show that KAN-PCA achieves a reconstruction R^2 of 66.57%, compared to 62.99% for classical PCA with the same 3 factors, while matching PCA out-of-sample after correcting for data leakage in the training procedure.

FI-KAN: Fractal Interpolation Kolmogorov-Arnold Networks

Author: Gnankan Landry Regis N’guessan

Abstract: Kolmogorov-Arnold Networks (KAN) employ B-spline bases on a fixed grid, providing no intrinsic multi-scale decomposition for non-smooth function approximation. We introduce Fractal Interpolation KAN (FI-KAN), which incorporates learnable fractal interpolation function (FIF) bases from iterated function system (IFS) theory into KAN. Two variants are presented: Pure FI-KAN (Barnsley, 1986) replaces B-splines entirely with FIF bases; Hybrid FI-KAN (Navascues, 2005) retains the B-spline path and adds a learnable fractal correction. The IFS contraction parameters give each edge a differentiable fractal dimension that adapts to target regularity during training. On a Holder regularity benchmark ($α\in [0.2, 2.0]$), Hybrid FI-KAN outperforms KAN at every regularity level (1.3x to 33x). On fractal targets, FI-KAN achieves up to 6.3x MSE reduction over KAN, maintaining 4.7x advantage at 5 dB SNR. On non-smooth PDE solutions (scikit-fem), Hybrid FI-KAN achieves up to 79x improvement on rough-coefficient diffusion and 3.5x on L-shaped domain corner singularities. Pure FI-KAN’s complementary behavior, dominating on rough targets while underperforming on smooth ones, provides controlled evidence that basis geometry must match target regularity. A fractal dimension regularizer provides interpretable complexity control whose learned values recover the true fractal dimension of each target. These results establish regularity-matched basis design as a principled strategy for neural function approximation.

KAN-LSTM: Benchmarking Kolmogorov-Arnold Networks for Cyber Security Threat Detection in IoT Networks

Author: Mohammed Hassanin

Abstract: By utilising their adaptive activation functions, Kolmogorov-Arnold Networks (KANs) can be applied in a novel way for the diverse machine learning tasks, including cyber threat detection. KANs substitute conventional linear weights with spline-parametrized univariate functions, which allows them to learn activation patterns dynamically, inspired by the Kolmogorov-Arnold representation theorem. In a network traffic data, we show that KANs perform better than traditional Multi-Layer Perceptrons (MLPs), yielding more accurate results with a significantly less number of learnable parameters. We also propose KAN-LSTM model to combine advantages of spatial and temporal encoding. The suggested methodology highlights the potential of KANs as an effective tool in detecting cyber threats and offers up new directions for adaptive defensive models. Lastly, we conducted experiments on three main dataset, UNSW-NB15, NSL-KDD, and CICID2017, as well as we developed a new dataset combined from IOT-BOT, NSL-KDD, and CICID2017 to present a stable, unbiased, large-scale dataset with diverse traffic patterns. The results show the superiority of KAN-LSTM and then KAN models over the traditional deep learning models. The source code is available at GitHub repository

April

Explainable Functional Relation Discovery for Battery State-of-Health Using Kolmogorov-Arnold Network

Authors: Sanchita Ghosh, Tanushree Roy

Abstract: Battery health management is heavily dependent on reliable State-of-Health (SoH) estimation to ensure battery safety with maximized energy utilization. Although SoH estimation can effectively track battery degradation, it requires continuous battery data acquisition. In addition, model-based SoH estimation methods rely on accurate battery model knowledge, whereas data-driven approaches often suffer from limited interpretability. In contrast, analytical characterization of SoH will offer a direct and tractable handle on battery performance degradation, while also establishing a foundation for further analytical studies toward effective battery health management. Thus, in this work, we propose a Kolmogorov Arnold Network (KAN)-based data-driven pipeline to establish a functional relationship for SoH degradation using battery temperature data. Specifically, we learn long-term battery thermal dynamics and battery heat generation via learnable activation functions of our KAN model. We utilize the learned mapping to obtain an explicit functional relationship between SoH degradation and cycle number. The proposed pipeline was validated using real-world data, yielding a closed-form analytical formula of SoH degradation with high accuracy.

Light-ResKAN: A Parameter-Sharing Lightweight KAN with Gram Polynomials for Efficient SAR Image Recognition

Authors: Pan Yi, Weijie Li, Xiaodong Chen, Jiehua Zhang, Li Liu, Yongxiang Liu

Abstract: Synthetic Aperture Radar (SAR) image recognition is vital for disaster monitoring, military reconnaissance, and ocean observation. However, large SAR image sizes hinder deep learning deployment on resource-constrained edge devices, and existing lightweight models struggle to balance high-precision feature extraction with low computational requirements. The emerging Kolmogorov-Arnold Network (KAN) enhances fitting by replacing fixed activations with learnable ones, reducing parameters and computation. Inspired by KAN, we propose Light-ResKAN to achieve a better balance between precision and efficiency. First, Light-ResKAN modifies ResNet by replacing convolutions with KAN convolutions, enabling adaptive feature extraction for SAR images. Second, we use Gram Polynomials as activations, which are well-suited for SAR data to capture complex non-linear relationships. Third, we employ a parameter-sharing strategy: each kernel shares parameters per channel, preserving unique features while reducing parameters and FLOPs. Our model achieves 99.09%, 93.01%, and 97.26% accuracy on MSTAR, FUSAR-Ship, and SAR-ACD datasets, respectively. Experiments on MSTAR resized to $1024 \times 1024$ show that compared to VGG16, our model reduces FLOPs by $82.90 \times$ and parameters by $163.78 \times$. This work establishes an efficient solution for edge SAR image recognition.

Hardware-Oriented Inference Complexity of Kolmogorov-Arnold Networks

Authors: Bilal Khalid, Pedro Freire, Sergei K. Turitsyn, Jaroslaw E. Prilepsky

Abstract: Kolmogorov-Arnold Networks (KANs) have recently emerged as a powerful architecture for various machine learning applications. However, their unique structure raises significant concerns regarding their computational overhead. Existing studies primarily evaluate KAN complexity in terms of Floating-Point Operations (FLOPs) required for GPU-based training and inference. However, in many latency-sensitive and power-constrained deployment scenarios, such as neural network-driven non-linearity mitigation in optical communications or channel state estimation in wireless communications, training is performed offline and dedicated hardware accelerators are preferred over GPUs for inference. Recent hardware implementation studies report KAN complexity using platform-specific resource consumption metrics, such as Look-Up Tables, Flip-Flops, and Block RAMs. However, these metrics require a full hardware design and synthesis stage that limits their utility for early-stage architectural decisions and cross-platform comparisons. To address this, we derive generalized, platform-independent formulae for evaluating the hardware inference complexity of KANs in terms of Real Multiplications (RM), Bit Operations (BOP), and Number of Additions and Bit-Shifts (NABS). We extend our analysis across multiple KAN variants, including B-spline, Gaussian Radial Basis Function (GRBF), Chebyshev, and Fourier KANs. The proposed metrics can be computed directly from the network structure and enable a fair and straightforward inference complexity comparison between KAN and other neural network architectures.

SPARK-IL: Spectral Retrieval-Augmented RAG for Knowledge-driven Deepfake Detection via Incremental Learning

Authors: Hessen Bougueffa Eutamene, Abdellah Zakaria Sellam, Abdelmalik Taleb-Ahmed, Abdenour Hadid

Abstract: Detecting AI-generated images remains a significant challenge because detectors trained on specific generators often fail to generalize to unseen models; however, while pixel-level artifacts vary across models, frequency-domain signatures exhibit greater consistency, providing a promising foundation for cross-generator detection. To address this, we propose SPARK-IL, a retrieval-augmented framework that combines dual-path spectral analysis with incremental learning by utilizing a partially frozen ViT-L/14 encoder for semantic representations alongside a parallel path for raw RGB pixel embeddings. Both paths undergo multi-band Fourier decomposition into four frequency bands, which are individually processed by Kolmogorov-Arnold Networks (KAN) with mixture-of-experts for band-specific transformations before the resulting spectral embeddings are fused via cross-attention with residual connections. During inference, this fused embedding retrieves the $k$ nearest labeled signatures from a Milvus database using cosine similarity to facilitate predictions via majority voting, while an incremental learning strategy expands the database and employs elastic weight consolidation to preserve previously learned transformations. Evaluated on the UniversalFakeDetect benchmark across 19 generative models – including GANs, face-swapping, and diffusion methods – SPARK-IL achieves a 94.6\% mean accuracy, with the code to be publicly released at https://github.com/HessenUPHF/SPARK-IL.

Efficient Convexification of Kolmogorov-Arnold Networks with Polynomial Functional Forms Via a Continuous Graham Scan Approach

Authors: Tianwei Li, Daniel Ovalle, Barnabas Poczos, Carl Laird, Ignacio Grossmann, Javier Pena

Abstract: Deterministic global optimization of nonlinear models is important in many scientific and engineering applications. This framework typically involves repeatedly solving convex relaxations of the nonconvex problem, meaning that the strength of the relaxations and the cost of computing them directly determine overall efficiency and solution quality. In this work, we develop a tailored continuous convexification framework for Kolmogorov-Arnold Networks in which the univariate components are polynomial functions. By exploiting the additive separable structure of this architecture, the relaxation problem reduces to computing tight convex envelopes of univariate polynomials. We propose a continuous variant of the classical Graham Scan that constructs these envelopes exactly by identifying the bitangents of the polynomial convex hull without discretization or factorable reformulations. We establish the correctness of the algorithm and characterize its computational complexity, and show how these envelopes can be combined to construct strong convex relaxations for polynomial KANs. Computational results demonstrate that the proposed relaxations are both strong and robust, often producing bounds that are comparable, or even orders of magnitude tighter than relaxations of state-of-the-art global optimization solvers while remaining computationally efficient.

Interpretation of Crystal Energy Landscapes with Kolmogorov-Arnold Networks

Authors: Gen Zu, Ning Mao, Claudia Felser, Yang Zhang

Abstract: Characterizing crystalline energy landscapes is essential to predicting thermodynamic stability, electronic structure, and functional behavior. While machine learning (ML) enables rapid property predictions, the “black-box” nature of most models limits their utility for generating new scientific insights. Here, we introduce Kolmogorov-Arnold Networks (KANs) as an interpretable framework to bridge this gap. Unlike conventional neural networks with fixed activation functions, KANs employ learnable functions that reveal underlying physical relationships. We developed the Element-Weighted KAN, a composition-only model that achieves state-of-the-art accuracy in predicting formation energy, band gap, and work function across large-scale datasets. Crucially, without any explicit physical constraints, KANs uncover interpretable chemical trends aligned with the periodic table and quantum mechanical principles through embedding analysis, correlation studies, and principal component analysis. These results demonstrate that KANs provide a powerful framework with high predictive performance and scientific interpretability, establishing a new paradigm for transparent, chemistry-based materials informatics.

Hyperfastrl: Hypernetwork-based reinforcement learning for unified control of parametric chaotic PDEs

Authors: Anil Sapkota, Omer San

Abstract: Spatiotemporal chaos in fluid systems exhibits severe parametric sensitivity, rendering classical adjoint-based optimal control intractable because each operating regime requires recomputing the control law. We address this bottleneck with hyperFastRL, a parameter-conditioned reinforcement learning framework that leverages Hypernetworks to shift from tuning isolated controllers per-regime to learning a unified parametric control manifold. By mapping a physical forcing parameter μ directly to the weights of a spatial feedback policy, the architecture cleanly decouples parametric adaptation from spatial boundary stabilization. To overcome the extreme variance inherent to chaotic reward landscapes, we deploy a pessimistic distributional value estimation over a massively parallel environment ensemble. We evaluate three Hypernetwork functional forms, ranging from residual MLPs to periodic Fourier and Kolmogorov-Arnold (KAN) representations, on the Kuramoto-Sivashinsky equation under varying spatial forcing. All forms achieve robust stabilization. KAN yields the most consistent energy-cascade suppression and tracking across unseen parametrizations, while Fourier networks exhibit worse extrapolation variability. Furthermore, leveraging high-throughput parallelization allows us to intentionally trade a fraction of peak asymptotic reward for a 37% reduction in training wall-clock time, identifying an optimal operating regime for practical deployment in complex, parameter-varying chaotic PDEs.

Small-scale photonic Kolmogorov-Arnold networks using standard telecom nonlinear modules

Authors: Luca Nogueira Calçado, Sergei K. Turitsyn, Egor Manuylovich

Abstract: Photonic neural networks promise ultrafast inference, yet most architectures rely on linear optical meshes with electronic nonlinearities, reintroducing optical-electrical-optical bottlenecks. Here we introduce small-scale photonic Kolmogorov-Arnold networks (SSP-KANs) implemented entirely with standard telecommunications components. Each network edge employs a trainable nonlinear module composed of a Mach-Zehnder interferometer, semiconductor optical amplifier, and variable optical attenuators, providing a four-parameter transfer function derived from gain saturation and interferometric mixing. Despite this constrained expressivity, SSP-KANs comprising only a few optical modules achieve strong nonlinear inference performance across classification, regression, and image recognition tasks, approaching software baselines with significantly fewer parameters. A four-module network achieves 98.4\% accuracy on nonlinear classification benchmarks inaccessible to linear models. Performance remains robust under realistic hardware impairments, maintaining high accuracy down to 6-bit input resolution and 14 dB signal-to-noise ratio. By using a fully differentiable physics model for end-to-end optimisation of optical parameters, this work establishes a practical pathway from simulation to experimental demonstration of photonic KANs using commodity telecom hardware.

Gait Recognition with Temporal Kolmogorov-Arnold Networks

Authors: Mohammed Asad, Dinesh Kumar Vishwakarma

Abstract: Gait recognition is a biometric modality that identifies individuals from their characteristic walking patterns. Unlike conventional biometric traits, gait can be acquired at a distance and without active subject cooperation, making it suitable for surveillance and public safety applications. Nevertheless, silhouette-based temporal models remain sensitive to long sequences, observation noise, and appearance-related covariates. Recurrent architectures often struggle to preserve information from earlier frames and are inherently sequential to optimize, whereas transformer-based models typically require greater computational resources and larger training sets and may be sensitive to irregular sequence lengths and noisy inputs. These limitations reduce robustness under clothing variation, carrying conditions, and view changes, while also hindering the joint modeling of local gait cycles and longer-term motion trends. To address these challenges, we introduce a Temporal Kolmogorov-Arnold Network (TKAN) for gait recognition. The proposed model replaces fixed edge weights with learnable one-dimensional functions and incorporates a two-level memory mechanism consisting of short-term RKAN sublayers and a gated long-term pathway. This design enables efficient modeling of both cycle-level dynamics and broader temporal context while maintaining a compact backbone. Experiments on the CASIA-B dataset indicate that the proposed CNN+TKAN framework achieves strong recognition performance under the reported evaluation setting.

Hardware-Efficient Neuro-Symbolic Networks with the Exp-Minus-Log Operator

Author: Eymen Ipek

Abstract: Deep neural networks (DNNs) deliver state-of-the-art accuracy on regression and classification tasks, yet two structural deficits persistently obstruct their deployment in safety-critical, resource-constrained settings: (i) opacity of the learned function, which precludes formal verification, and (ii) reliance on heterogeneous, library-bound activation functions that inflate latency and silicon area on edge hardware. The recently introduced Exp-Minus-Log (EML) Sheffer operator, eml(x, y) = exp(x) - ln(y), was shown by Odrzywolek (2026) to be sufficient - together with the constant 1 - to express every standard elementary function as a binary tree of identical nodes. We propose to embed EML primitives inside conventional DNN architectures, yielding a hybrid DNN-EML model in which the trunk learns distributed representations and the head is a depth-bounded, weight-sparse EML tree whose snapped weights collapse to closed-form symbolic sub-expressions. We derive the forward equations, prove computational-cost bounds, analyse inference and training acceleration relative to multilayer perceptrons (MLPs) and physics-informed neural networks (PINNs), and quantify the trade-offs for FPGA/analog deployment. We argue that the DNN-EML pairing closes a literature gap: prior neuro-symbolic and equation-learner approaches (EQL, KAN, AI-Feynman) work with heterogeneous primitive sets and do not exploit a single hardware-realisable Sheffer element. A balanced assessment shows that EML is unlikely to accelerate training, and on commodity CPU/GPU it is also unlikely to accelerate inference; however, on a custom EML cell (FPGA logic block or analog circuit) the asymptotic latency advantage can reach an order of magnitude with simultaneous gain in interpretability and formal-verification tractability.

From Zero to Detail: A Progressive Spectral Decoupling Paradigm for UHD Image Restoration with New Benchmark

Authors: Chen Zhao, Yunzhe Xu, Zhizhou Chen, Enxuan Gu, Kai Zhang, Xiaoming Liu, Jian Yang, Ying Tai

Abstract: Ultra-high-definition (UHD) image restoration poses unique challenges due to the high spatial resolution, diverse content, and fine-grained structures present in UHD images. To address these issues, we introduce a progressive spectral decomposition for the restoration process, decomposing it into three stages: zero-frequency \textbf{enhancement}, low-frequency \textbf{restoration}, and high-frequency \textbf{refinement}. Based on this formulation, we propose a novel framework, \textbf{ERR}, which integrates three cooperative sub-networks: the zero-frequency enhancer (ZFE), the low-frequency restorer (LFR), and the high-frequency refiner (HFR). The ZFE incorporates global priors to learn holistic mappings, the LFR reconstructs the main content by focusing on coarse-scale information, and the HFR adopts our proposed frequency-windowed Kolmogorov-Arnold Network (FW-KAN) to recover fine textures and intricate details for high-fidelity restoration. To further advance research in UHD image restoration, we also construct a large-scale, high-quality benchmark dataset, \textbf{LSUHDIR}, comprising 82{,}126 UHD images with diverse scenes and rich content. Our proposed methods demonstrate superior performance across a range of UHD image restoration tasks, and extensive ablation studies confirm the contribution and necessity of each module. Project page: https://github.com/NJU-PCALab/ERR.

Singularity Formation: Synergy in Theoretical, Numerical and Machine Learning Approaches

Author: Yixuan Wang

Abstract: This thesis develops numerical and theoretical approaches for understanding and analyzing singularity formation in Partial Differential Equations (PDEs). The singularity formation in the Navier-Stokes Equation (NSE) is famously challenging as one of the seven Clay Prize problems. Unlike simpler equations such as the Nonlinear Heat (NLH) or Keller-Segel (KS) equations, where formal asymptotics near blowup are better understood, the intrinsic complexity of NSE makes quantitative analytical treatment difficult, if not impossible, without numerical guidance. Building on numerical insights, we introduce a robust analytical framework to simplify and systematize pen-and-paper proofs for simpler singular PDEs. We present a novel approach based on enforcing vanishing modulation conditions for perturbations around approximate blowup profiles, complemented by singularly weighted energy estimates. We demonstrate the efficacy of our method on PDEs with complicated asymptotics, such as NLH and the Complex Ginzburg-Landau (CGL) equation, and address the open problem of singularity formation in the 3D KS equation with logistic damping. We develop and refine numerical approaches that facilitate deeper insights into singularity formation. We demonstrate that machine learning methods significantly enhance our capability to identify and characterize potential blowup solutions with high precision. We improve on existing Physics-Informed Neural Network (PINN) and Neural Operator (NO) frameworks. Moreover, we present a novel machine learning paradigm, the Kolmogorov-Arnold Network (KAN) architecture, whose interpretability and excellent scaling properties are achieved through learnable nonlinearities.

Scale-Parameter Selection in Gaussian Kolmogorov-Arnold Networks

Authors: Amir Noorizadegan, Sifan Wang

Abstract: Kolmogorov–Arnold Networks (KANs) have recently attracted attention as edge-based neural architectures in which learnable univariate functions replace conventional fixed activation functions. A key source of flexibility in KANs is the choice of basis functions used to parameterize the learnable edge functions. In this context, Gaussian basis functions provide a simple and efficient alternative to splines. However, their performance depends strongly on the scale (shape) parameter (ε), whose role has not been studied systematically. In this paper, we investigate how (ε) affects Gaussian KANs through first-layer feature geometry, conditioning, and approximation behavior. Our central observation is that scale selection is governed primarily by the first layer, since it is the only layer constructed directly on the input domain and any loss of distinguishability introduced there cannot be recovered by later layers. From this viewpoint, we analyze the first-layer feature matrix and identify a practical operating interval, [ ε\in \left[\frac{1}{G-1},\frac{2}{G-1}\right], ] where (G) denotes the number of Gaussian centers. We interpret this interval not as a universal optimality result, but as a stable and effective design rule, and validate it through brute-force sweeps over (ε) across function-approximation problems with different collocation densities, grid resolutions, network architectures, and input dimensions, as well as physics-informed problems. We further show that this range is useful for fixed-scale selection, variable-scale constructions, constrained training of (ε), and efficient scale search using early training MSE. In this way, the paper positions scale selection as a practical design principle for Gaussian KANs rather than as an ad hoc hyperparameter choice.

LTBs-KAN: Linear-Time B-splines Kolmogorov-Arnold Networks

Authors: Eduardo Said Merin-Martinez, Andres Mendez-Vazquez, Eduardo Rodriguez-Tello

Abstract: Kolmogorov-Arnold Networks (KANs) are a recent neural network architecture offering an alternative to Multilayer Perceptrons (MLPs) with improved explainability and expressibility. However, KANs are significantly slower than MLPs due to the recursive nature of B-spline function computations, limiting their application. This work addresses these issues by proposing a novel base-spline Linear-Time B-splines Kolmogorov-Arnold Network (LTBs-KAN) with linear complexity. Unlike previous methods that rely on the Boor-Mansfield-Cox spline algorithm or other computationally intensive mathematical functions, our approach significantly reduces the computational burden. Additionally, we further reduce model’s parameter through product-of-sums matrix factorization in the forward pass without sacrificing performance. Experiments on MNIST, Fashion-MNIST and CIFAR-10 demonstrate that LTBs-KAN achieves good time complexity and parameter reduction, when used as building architectural blocks, compared to other KAN implementations.

KAConvNet: Kolmogorov-Arnold Convolutional Networks for Vision Recognition

Authors: Zhaoxiang Liu, Zhicheng Ma, Kaikai Zhao, Kai Wang, Shiguo Lian

Abstract: The Convolutional Neural Networks (CNNs) have been the dominant and effective approach for general computer vision tasks. Recently, Kolmogorov-Arnold neural networks (KANs), based on the Kolmogorov-Arnold representation theorem, have shown potential to replace Multi-Layer Perceptrons (MLPs) in deep learning. KANs, which use learnable nonlinear activations on edges and simple summation on nodes, offer fewer parameters and greater explainability compared to MLPs. However, there has been limited exploration of integrating the Kolmogorov-Arnold representation theorem with convolutional methods for computer vision tasks. Existing attempts have merely replaced learnable activation functions with weights, undermining KANs’ theoretical foundation and limiting their potential effectiveness. Additionally, the B-spline curves used in KANs suffer from computational inefficiency and a tendency to overfit. In this paper, we propose a novel Kolmogorov-Arnold Convolutional Layer that deeply integrates the Kolmogorov-Arnold representation theorem with convolution. This layer provides stronger method interpretability because it is based on established mathematical theorems and its design has theoretical alignment. Building on the Kolmogorov-Arnold Convolutional Layer, we design an efficient network architecture called KAConvNet, which outperforms existing methods combining KAN and convolution, and achieves competitive performance compared to mainstream ViTs and CNNs. We believe that our work offers valuable insight into the field of artificial intelligence and will inspire the development of more innovative CNNs in the 2020s. The code is publicly available at https://github.com/UnicomAI/KAConvNet.

Autocorrelation Reintroduces Spectral Bias in KANs for Time Series Forecasting

Authors: Chen Zeng, Jiahui Wang, Qiao Wang

Abstract: Existing theory suggests that Kolmogorov-Arnold Networks (KANs) can overcome the spectral bias commonly observed in neural networks under the assumption that inputs are statistically independent. However, this assumption does not hold in time series forecasting (TSF), where inputs are lagged observations with strong temporal autocorrelation. Through theoretical analysis and empirical validation, we obtain an unexpected finding: temporal autocorrelation reintroduces spectral bias in KANs, and the bias becomes increasingly pronounced as the degree of autocorrelation increases. This suggests that standard KANs may face substantial difficulties in TSF with strongly autocorrelated inputs. To address this problem, we introduce the Discrete Cosine Transform (DCT) to reduce the correlations among the network inputs. As expected, experimental results reveal that DCT preprocessing substantially reduces the observed low-frequency preference in TSF. This result also corroborates that the spectral bias of KANs in TSF tasks is indeed induced by the autocorrelation among input variables.

Partition-of-Unity Gaussian Kolmogorov-Arnold Networks

Author: Amir Noorizadegan

Abstract: Gaussian basis functions provide an efficient and flexible alternative to spline activations in KANs. In this work, we introduce the partition-of-unity Gaussian KAN (PU-GKAN), a Shepard-type normalized Gaussian KAN in which the Gaussian basis values on each edge are divided by their local sum over fixed centers. This produces a partition-of-unity feature map with trainable coefficients, while preserving the standard edge-based KAN structure. The normalized construction gives exact constant reproduction at the edge level and admits an explicit finite-feature kernel interpretation. We formulate both the standard Gaussian KAN (GKAN) and PU-GKAN from a finite-feature and additive-kernel viewpoint, making the induced layer kernels and empirical feature matrices explicit. Using the first-layer feature matrix as the reference object, we adopt a practical scale-selection interval for (ε), with the lower endpoint determined by adjacent-center overlap and the upper endpoint determined by a conservative conditioning threshold. Numerical experiments show that PU-GKAN reduces sensitivity to (ε), improves validation accuracy for most smooth and moderately non-smooth targets, and gives more stable training behavior. The benefit persists across sample-size and center-number sweeps, higher-dimensional architectures, Matérn RBF bases, and physics-informed examples involving Helmholtz and wave equations. These results indicate that Shepard-type partition-of-unity normalization is a simple and effective stabilization mechanism for RBF-based KANs.

Necessary and sufficient conditions for universality of Kolmogorov-Arnold networks

Author: Vugar Ismailov

Abstract: We analyze the universal approximation property of Kolmogorov-Arnold Networks (KANs) in terms of their edge functions. If these functions are all affine, then universality clearly fails. How many non-affine functions are needed, in addition to affine ones, to ensure universality? We show that a single one suffices. More precisely, we prove that deep KANs in which all edge functions are either affine or equal to a fixed continuous function $σ$ are dense in $C(K)$ for every compact set $K\subset\mathbb{R}^n$ if and only if $σ$ is non-affine. In contrast, for KANs with exactly two hidden layers, universality holds if and only if $σ$ is nonpolynomial. We further show that the full class of affine functions is not required; it can be replaced by a finite set without affecting universality. In particular, in the nonpolynomial case, a fixed family of five affine functions suffices when the depth is arbitrary. More generally, for every continuous non-affine function $σ$, there exists a finite affine family $A_σ$ such that deep KANs with edge functions in $A_σ\cup{σ}$ remain universal. We also prove that KANs with the spline-based edge parameterization introduced by Liu et al.~\cite{Liu2024} are universal approximators in the classical sense, even when the spline degree and knot sequence are fixed in advance.

DecompKAN: Decomposed Patch-KAN for Long-Term Time Series Forecasting

Author: Naveen Mysore

Abstract: Accurate time series forecasting in scientific domains such as climate modeling, physiological monitoring, and energy systems benefits from both competitive predictions and model transparency. This work proposes DecompKAN, a lightweight attention-free architecture that combines trend-residual decomposition, channel-wise patching, learned instance normalization, and B-spline Kolmogorov-Arnold Network (KAN) edge functions. Each KAN edge learns an explicit, inspectable 1D scalar function over learned patch-embedding coordinates that can be directly visualized. On standard benchmarks, DecompKAN achieves best or tied-best MSE on 15 of 32 dataset-horizon combinations among selected published baselines, and achieves best or tied-best MSE on 20 of 36 comparisons under a controlled same-recipe evaluation across 9 datasets including the physiological PPG-DaLiA benchmark. The architecture shows particular strength on datasets with smooth temporal dynamics (Solar -17%, ECL -10% vs. iTransformer, Weather) and physiological time series. Visualization of learned edge functions reveals qualitatively different latent nonlinearities across domains. Ablation analysis shows that the architectural pipeline (decomposition, patching, normalization) drives performance more than the choice of nonlinear layer, while the KAN formulation enables inspection of learned latent transformations.

Layer-wise Lipschitz-Product Control for Deep Kolmogorov–Arnold Network Representations of Compositionally Structured Functions

Author: Aleksander Tankman

Abstract: We prove that any continuous function f from [0,1]^n to R representable by a finite computation tree with N internal nodes and compositional sparsity s = O(1) admits a deep Kolmogorov-Arnold Network (KAN) representation. Each internal node is realised by a primitive KAN block with controlled block depth and Lipschitz product. The layer-wise Lipschitz product satisfies the primary domain-sensitive bound independent of the input dimension n. It simplifies to P(KAN_f) <= max(C,1)^L_f with L_f <= c_max * N. For the standard operations {+,-,x,sin,cos} with x nodes on [0,1]-bounded inputs we obtain P(KAN) <= 1. Layer widths satisfy n_l <= n + 2 w_max * N. The uniform approximation error is bounded by N * max(C,1)^d(f) * epsilon_Op (simplifies when C* <=1). For f in C^m we obtain optimal B-spline rates. Range bounds are also derived (B_f <= N+1 for additive trees). This addresses the gap on Lipschitz control in deep KAN stacks noted by Liu et al. (2024). Experiments confirm P(KAN)=1.0 for several compositionally structured functions.

May

RoboKA: KAN Informed Multimodal Learning for RoboCall Surveillance System

Authors: Nitin Choudhury, Nikhil Kumar, Aditya Kumar Sinha, Abhijeet Anand, Hossein Salemi, Orchid Chetia Phukan, Hemant Purohit, Arun Balaji Buduru

Abstract: Wide exploration on robocall surveillance research is hindered due to limited access to public datasets, due to privacy concerns. In this work, we first curate Robo-SAr, a synthetic robocall dataset designed for robocall surveillance research. Robo-SAr comprises of ~200 unwanted and ~1200 legitimate synthetic robocall samples across three realistic adversarial axes: psycholinguistics-manipulated transcripts, emotion-eliciting speech, and cloned voices. We further propose RoboKA, a Kolmogorov-Arnold Network (KAN)-based multimodal fusion framework designed to model structured nonlinear interactions between acoustic and linguistic cues that characterize diverse adversarial robocall strategies. RoboKA first leverages cross-modal contrastive learning to align latent modality representations and feeds the resulting embeddings to a KAN-projection head for final classification. We benchmark RoboKA against strong unimodal and multimodal baselines in both in-domain and out-of-domain setups, finding RoboKA to surpass all baselines in terms of recall and F1-score.

SRGAN-CKAN: Expressive Super-Resolution with Nonlinear Functional Operators under Minimal Resources

Authors: Roberto Isai Navaro-Aviña, Eduardo Said Merin-Martinez, Andres Mendez-Vazquez, Eduardo Rodriguez-Tello

Abstract: Single-Image Super-Resolution (SISR) aims to reconstruct a High-Resolution (HR) image from a Low-Resolution (LR) observation, a fundamentally ill-posed problem where high-frequency details are severely degraded at large upscaling factors. Recent advances have been driven by transformer-based architectures and diffusion models improve global context modeling and perceptual quality at the cost of increased computational complexity. In contrast, this work focuses on enhancing the expressivity of local operators under minimal resources. We propose SRGAN–CKAN, a hybrid super-resolution framework that integrates Convolutional Kolmogorov–Arnold Networks (CKAN) into an adversarial learning setting reformulating convolution as a nonlinear patch-based transformation. The proposed operator replaces linear local mappings with spline-based functional representations, allowing expressive modeling of complex local structures and high-frequency textures using minimal hardware resources. Experimental results demonstrate that the proposed approach improves perceptual quality while preserving reconstruction fidelity, achieving a favorable balance between distortion-based and perceptual metrics. These results are obtained under constrained computational settings, highlighting the efficiency of the proposed formulation. Overall, this work introduces a complementary direction to existing approaches by improving the representational power of local transformations, providing an efficient and scalable alternative to globally intensive architectures.

KANs need curvature: penalties for compositional smoothness

Author: James Bagrow

Abstract: Kolmogorov-Arnold networks (KANs) offer a potent combination of accuracy and interpretability, thanks to their compositions of learnable univariate activation functions. However, the activations of well-fitting KANs tend to exhibit pathologically high-curvature oscillations, making them difficult to interpret, and standard regularization penalties do not prevent this. Here we derive a basis-agnostic curvature penalty and show that penalized models can maintain accuracy while achieving substantially smoother activations. Accounting for how function composition shapes curvature, we prove an upper bound on the full model’s curvature relative to the curvature penalty, and use this to motivate richer forms of penalties. Scientific machine learning is increasingly bottlenecked by the trade-off between accuracy and interpretability. Results such as ours that improve interpretability without sacrificing accuracy will further strengthen KANs as a practical tool for both prediction and insight.

Generative Quantum-inspired Kolmogorov-Arnold Eigensolver

Authors: Yu-Cheng Lin, Yu-Chao Hsu, I-Shan Tsai, Chun-Hua Lin, Kuo-Chung Peng, Jiun-Cheng Jiang, Yun-Yuan Wang, Tzung-Chi Huang, Tai-Yue Li, Kuan-Cheng Chen, Samuel Yen-Chi Chen, Nan-Yow Chen

Abstract: High-performance computing (HPC) is increasingly important for scalable quantum chemistry workflows that couple classical generative models, quantum circuit simulation, and selected configuration interaction postprocessing. We present the generative quantum-inspired Kolmogorov-Arnold eigensolver (GQKAE), a parameter-efficient extension of the generative quantum eigensolver (GQE) for quantum chemistry. GQKAE replaces the parameter-heavy feed-forward network components in GPT-style generative eigensolvers with hybrid quantum-inspired Kolmogorov-Arnold network modules, forming a compact HQKANsformer backbone. The method preserves autoregressive operator selection and the quantum-selected configuration interaction evaluation pipeline, while using single-qubit DatA Re-Uploading ActivatioN modules to provide expressive nonlinear mappings. Numerical benchmarks on H4, N2, LiH, C2H6, H2O, and the H2O dimer show that GQKAE achieves chemical accuracy comparable to the GPT-based GQE architecture, while reducing trainable parameters and memory by approximately 66% and improving wall-time performance. For strongly correlated systems such as N2 and LiH, GQKAE also improves convergence behavior and final energy errors. These results indicate that quantum-inspired Kolmogorov-Arnold networks can reduce classical-side overhead while preserving circuit-generation quality, offering a scalable route for HPC-quantum co-design on near-term quantum platforms.

Temporal Functional Circuits: From Spline Plots to Faithful Explanations in KAN Forecasting

Author: Naveen Mysore

Abstract: Unlike MLPs, Kolmogorov-Arnold Networks (KANs) expose explicit learnable edge functions on every connection, enabling mechanistic explanation in time-series forecasting. This paper introduces Temporal Functional Circuits, a framework that transforms KAN edge functions from latent visualizations into faithful, temporally grounded explanations. Built on a gated residual KAN that decomposes forecasts into a linear base and a sparsely activated KAN correction, the framework (i) maps each edge to input lags via output-aware attribution, (ii) ranks edges by learned activation range, and (iii) validates faithfulness through edge-level interventions including zeroing and spline removal. Removing the learned B-spline component while retaining the base SiLU term degrades forecasts, providing evidence that the spline shape itself carries predictive value beyond the base activation. On four synthetic regimes of increasing complexity, the learned gate opens progressively wider as signal complexity grows. On regime-switching signals, gated KAN achieves 59% lower MSE than linear-only models. Across eight benchmarks, the gated architecture is competitive with linear, attention, and MLP alternatives, while providing interpretable edge functions that MLP-based corrections cannot offer.

Deep-Koopman-KANDy: Dictionary Discovery for Deep-Koopman Operators with Kolmogorov-Arnold Networks for Dynamics

Authors: Kevin Slote, Erik Bollt, Jeremie Fish

Abstract: Symbolic library – or Koopman dictionary – selection is a fundamental challenge in data-driven dynamical systems. Extended Dynamic Mode Decomposition (EDMD), Sparse Identification of Nonlinear Dynamics (SINDy), and Kolmogorov–Arnold Networks for Dynamics (KANDy) all require the practitioner to commit to a function library at training time; Deep-Koopman Operators avoid this commitment but produce uninterpretable latent observables. We propose Deep-Koopman-KANDy, a structured approach to post-hoc symbolic dictionary readout that combines Deep-Koopman modeling with Kolmogorov-Arnold Networks for Dynamics (KANDy). The encoder and decoder of a Deep-Koopman Operator are replaced with two-layer Kolmogorov–Arnold Networks (KANs), and a level-set construction together with a chain-rule gradient identity exposes the compositional structure of the learned observables in a basis chosen \emph{after} training. We evaluate the method on the Lorenz system, the Chirikov standard map, the Ikeda map, and the Arnold cat map. On Lorenz it recovers the target dictionary ${x,y,z,xy,xz}$ with perfect recall and Jaccard score $0.79\pm0.06$; on the standard map it recovers a low-order Fourier basis matching the analytical structure; on Ikeda – which has no sparse polynomial representation – a misspecified polynomial readout still recovers the correct foliation coordinate $g\approx x^2+y^2$ together with a nontrivial outer function; and on the Arnold cat map – used as a negative control because finite-dimensional Koopman closure is provably impossible – the method fails to find a sparse closure, as expected.

Gated QKAN-FWP: Scalable Quantum-inspired Sequence Learning

Authors: Kuo-Chung Peng, Samuel Yen-Chi Chen, Jiun-Cheng Jiang, Chen-Yu Liu, En-Jui Kuo, Yun-Yuan Wang, Prayag Tiwari, Andrea Ceschini, Chi-Sheng Chen, Yu-Chao Hsu, Chun-Hua Lin, Tai-Yue Li, Antonello Rosato, Massimo Panella, Simon See, Saif Al-Kuwari, Kuan-Cheng Chen, Nan-Yow Chen, Hsi-Sheng Goan

Abstract: Fast Weight Programmers (FWPs) encode temporal dependencies through dynamically updated parameters rather than recurrent hidden states. Quantum FWPs (QFWPs) extend this idea with variational quantum circuits (VQCs), but existing implementations rely on multi-qubit architectures that are difficult to scale on noisy intermediate-scale quantum (NISQ) devices and expensive to simulate classically. We propose gated QKAN-FWP, a fast-weight framework that integrates FWP with Quantum-inspired Kolmogorov-Arnold Network (QKAN) using single-qubit data re-uploading circuits as learnable nonlinear activation, known as DatA Re-Uploading ActivatioN (DARUAN). We further introduce a scalar-gated fast-weight update rule that stabilizes parameter evolution, supported by a theoretical analysis of its adaptive memory kernel, geometric boundedness, and parallelizable gradient paths. We evaluate the framework across time-series benchmarks, MiniGrid reinforcement learning, and highlight real-world solar cycle forecasting as our main practical result. In the long-horizon setting with 528-month input window and 132-month forecast horizon, our 12.5k-parameter model achieves lower scaled Mean Square Error (MSE), peak amplitude error, and peak timing error than a suite of classical recurrent baselines with up to 13x more parameters, including Long Short-Term Memory (LSTM) networks (25.9k-89.1k parameters), WaveNet-LSTM (167k), Vanilla recurrent neural network (11.5k), and a Modified Echo State Network (132k). To validate NISQ compatibility, we further deploy the trained fast programmer on IonQ and IBM Quantum processors, recovering forecasting accuracy within 0.1% relative MSE of the noiseless simulator at 1024 shots. These results position gated QKAN-FWP as a scalable, parameter-efficient, and NISQ-compatible approach to quantum-inspired sequence modeling.

Geometric Kolmogorov–Arnold Network (GeoKAN)

Authors: Abhijit Sen, Bikram Keshari Parida, Giridas Maiti, Mahima Arya, Denys I. Bondar

Abstract: We introduce Geometric Kolmogorov–Arnold Networks (GeoKANs), a family of geometry-aware KAN-type models in which approximation is carried out in learned, geometry-adapted coordinates rather than in fixed Euclidean input coordinates. GeoKAN achieves this by learning a diagonal Riemannian metric that warps the input before basis expansion and feature mixing. The learned metric provides a geometric inductive bias through local length scaling and volume distortion, and in physics-informed settings it also affects the differential structure seen by the model. Within this framework, we develop three main variants, namely GeoKAN-NNMetric, GeoKAN-$γ$, and LM-KAN. For LM-KAN, we further consider three basis-specific versions, LM-KAN-RBF, LM-KAN-Wav, and LM-KAN-Fourier. These variants allow us to study geometry-aware KAN models both as general function approximators and as surrogates in physics-informed learning. By stretching regions with rapid variation and compressing smoother regions, GeoKAN reallocates representational resolution in a task-dependent manner, allowing the model to place capacity where it is most needed. As a result, GeoKAN is well suited to sharp, stiff, localized, and strongly non-uniform regimes arising in scientific machine learning and differential-equation problems.

Towards Intelligent Low-Altitude Wireless Network Deployment: Differentiable Channel Knowledge Map Construction and Trajectory Design

Authors: Le Zhao, Zesong Fei, Wenge Shi, Xinyi Wang, Jingxuan Huang, Jihao Luo, Yong Zeng

Abstract: Channel knowledge map (CKM) has emerged as a promising technique to leverage prior propagation knowledge in low-altitude wireless networks (LAWNs), yet state-of-the-art grid-based CKM construction methods struggle to support efficient LAWN deployment due to their lack of differentiability with respect to continuous locations of unmanned aerial vehicles (UAVs). To overcome this limitation, we propose a differentiable CKM-triggered trajectory optimization framework for LAWNs. Firstly, we propose a location-oriented CKM construction method that directly maps continuous spatial coordinates to channel gain. In particular, a shared convolutional neural network (CNN) is employed to encode high-level environmental features from conditional inputs. These features are then sampled based on location information to form a fused regressor-conditional multilayer perceptron (c-MLP) or conditional Kolmogorov-Arnold network (cKAN)-for channel gain prediction. We further propose a joint power, bandwidth, and trajectory optimization (JPBTO) method for multi-UAV systems, with the constructed differentiable CKM employed to evaluate the communication performance. The formulated non-convex problem is solved via alternating optimization and successive convex approximation. Numerical results show that the proposed framework enables location-aware differentiability of the CKM, while achieving higher accuracy than the methods without environmental features. Furthermore, the proposed CKM-JPBTO achieves a significantly higher minimum throughput than the conventional statistical channel model-based JPBTO.

Neural Operators as Efficient Function Interpolators

Authors: Vasilis Niarchos, Angelos Sirbu, Sokratis Trifinopoulos

Abstract: Neural operators (NOs) are designed to learn maps between infinite-dimensional function spaces. We propose a novel reframing of their use. By introducing an auxiliary base-space, any finite-dimensional function can be viewed as an operator acting by composition on functions of the base-space. Through a range of benchmarks on analytic functions of increasing complexity and dimensionality, we demonstrate that NOs can match or outperform standard multilayer perceptrons and Kolmogorov–Arnold Networks in accuracy while requiring significantly fewer parameters and training time. As a real-world application, we apply a two-dimensional Tensorized Fourier Neural Operator (TFNO) to the nuclear chart, learning a correction to state-of-the-art nuclear mass models as a partially observed residual field. A TFNO ensemble reaches a held-out root-mean-square error of 198.2 keV, placing it among the best recent neural-network approaches while retaining high parameter efficiency and short training times. More broadly, these results introduce NOs as a scalable framework for finite-dimensional function interpolation, from analytic benchmarks to structured scientific data.

KAN Text to Vision? The Exploration of Kolmogorov-Arnold Networks for Multi-Scale Sequence-Based Pose Animation from Sign Language Notation

Authors: Guanyi Du, Lintao Wang, Kun Hu, Ziyang Wang

Abstract: Sign language production from symbolic notation offers a scalable route to accessible sign animation. We present KANMultiSign, a multi-scale sequence generator that translates HamNoSys notation into two-dimensional human pose sequences. Our framework makes two complementary contributions. First, we introduce a coarse-to-fine generation strategy with multi-scale supervision: the model is first guided by an intermediate body–hand–face scaffold to encourage global structural coherence, and then refines fine-grained hand articulation to improve finger-level detail. Second, we investigate integrating Kolmogorov–Arnold Network modules into a Transformer backbone, using learnable univariate function primitives to model the highly non-linear mapping from discrete phonological symbols to continuous body kinematics with a compact parameterization. Experiments on multiple public corpora spanning Polish, German, Greek, and French sign languages show consistent reductions in dynamic time warping based joint error compared with a strong notation-to-pose baseline, while using substantially fewer parameters. Controlled ablations further indicate that KAN-based variants substantially reduce parameter count while maintaining competitive performance when coupled with multi-scale supervision, rather than serving as the main driver of accuracy gains. These findings position multi-scale supervision as the key mechanism for improving notation-conditioned pose generation, with KAN offering a compact alternative for efficient modeling. Our code will be publicly available.

Multi-Fidelity Emulation of Atmospheric Correction Coefficients with Physics-Guided Kolmogorov-Arnold Networks

Authors: Md Abdullah Al Mazid, Naphtali Rishe

Abstract: Atmospheric correction is a critical preprocessing step in optical remote sensing, but repeated high-fidelity radiative transfer simulations remain computationally expensive for dense look-up-table generation, sensitivity analysis, retrieval support, and operational preprocessing. This study presents a physics-aware multi-fidelity surrogate framework for emulating atmospheric correction coefficients using paired 6S and libRadtran simulations. Atmospheric and geometric states are sampled using Latin Hypercube Sampling, and both radiative transfer models are evaluated under matched conditions for Sentinel-2 bands using spectral-response-function-aware coefficient generation. The high-fidelity targets are path reflectance, total transmittance, and spherical albedo. A physics-guided Kolmogorov-Arnold Network, termed pKANrtm, receives the atmospheric state and low-fidelity 6S coefficients, predicts the residual relative to libRadtran, and reconstructs the high-fidelity coefficients. The pKANrtm model uses an Efficient-KAN architecture and is trained with a physics-consistency penalty applied in the original coefficient space. The proposed model is evaluated against state-of-the-art regression-based RTM surrogates. Across both standard and out-of-distribution evaluation settings, pKANrtm achieves the strongest overall predictive performance among the compared models. Runtime benchmarking demonstrates substantial acceleration relative to libRadtran, with GPU inference providing approximately four orders of magnitude single-sample speedup and batched inference reaching tens of thousands of samples per second. These results indicate that physics-aware multi-fidelity pKANrtm emulation provides an accurate, physically structured, and computationally efficient strategy for atmospheric correction coefficient generation.

Posterior Contraction Rates for Sparse Kolmogorov-Arnold Networks in Anisotropic Besov Spaces

Authors: Jeunghun Oh, Kyeongwon Lee, Jaeyong Lee, Lizhen Lin

Abstract: We study posterior contraction rates for sparse Bayesian Kolmogorov-Arnold networks (KANs) over anisotropic Besov spaces, providing a statistical foundation of KANs from a Bayesian point of view. We show that sparse Bayesian KANs equipped with spike-and-slab-type sparsity priors attain the near-minimax posterior contraction. In particular, the contraction rate depends on the intrinsic anisotropic smoothness of the underlying function. Moreover, by placing a hyperprior on a single model-size parameter, the resulting posterior adapts to unknown anisotropic smoothness and still achieves the corresponding near-minimax rate. A distinctive feature of our results, compared with those for standard sparse MLP-based models, is that the KAN depth can be kept fixed: owing to the flexibility of learnable spline edge functions, the required approximation complexity is controlled through the network width, spline-grid range and size, and parameter sparsity. Our analysis develops theoretical tools tailored to sparse spline-edge architectures, including approximation and complexity bounds for Bayesian KANs. We then extend to compositional Besov spaces and show that the contraction rates depend on layerwise smoothness and effective dimension of the underlying compositional structure, thereby effectively avoiding the curse of dimensionality. Together, the developed tools and findings advance the theoretical understanding of Bayesian neural networks and provide rigorous statistical foundations for KANs.

KAN-CL: Per-Knot Importance Regularization for Continual Learning with Kolmogorov-Arnold Networks

Author: Minjong Cheon

Abstract: Catastrophic forgetting remains the central obstacle in continual learning (CL): parameters shared across tasks interfere with one another, and existing regularization methods such as EWC and SI apply uniform penalties without awareness of which input region a parameter serves. We propose KAN-CL, a continual learning framework that exploits the compact-support spline parameterization of Kolmogorov-Arnold Networks (KANs) to perform importance-weighted anchoring at per-knot granularity. Deployed as a classification head on a convolutional backbone with standard EWC regularization on the backbone (bbEWC) KAN-CL achieves forgetting reductions of 88% and 93% over a head-only KAN baseline on Split-CIFAR-10/5T and Split-CIFAR-100/10T respectively, while matching or exceeding the accuracy of all baselines on both benchmarks. We further provide a Neural Tangent Kernel (NTK) analysis showing that KAN’s spline locality induces a structural rank deficit in the cross-task NTK, yielding a forgetting bound that holds even in the feature-learning regime. These results establish that combining an architecture with natural parameter locality (KAN head) with a complementary backbone regularizer (bbEWC) yields a compositional and principled approach to catastrophic forgetting.

ChannelKAN: Multi-Scale Dual-Domain Channel Prediction via Hybrid CNN-KAN Architecture

Authors: Nanqing Jiang, Zhangyao Song, Tao Guo, Xiaoyu Zhao, Yinfei Xu

Abstract: Accurate channel state information (CSI) prediction is essential for improving the reliability and spectral efficiency of massive MIMO-OFDM systems in high-mobility scenarios. Existing deep learning methods struggle to jointly capture short-term local variations and long-range nonlinear dependencies in CSI sequences. To address this challenge, we propose ChannelKAN, a hybrid CNN-KAN channel prediction model with multi-scale frequency domain information enhancement. The key insight is that CNNs and Kolmogorov-Arnold Networks (KANs) are naturally complementary: CNNs extract intra-time-step local spatial-frequency correlations, while KANs with learnable Chebyshev polynomial activations fit inter-time-step nonlinear temporal evolution in a holistic manner. Specifically, a dual-domain expansion module first generates complementary frequency-domain and delay-domain CSI representations. A multi-scale frequency information enhancement module then retains dominant spectral components at multiple scales to strengthen key features and suppress noise. Next, a CNN-KAN feature extraction module captures local correlations via cascaded convolutions and models long-range dependencies via Chebyshev KAN layers. Finally, a dual-domain fusion module adaptively integrates features from both branches to produce the prediction. Experiments on 3GPP-compliant QuaDRiGa datasets demonstrate that ChannelKAN outperforms RNN, LSTM, GRU, CNN, and Transformer baselines in normalized mean square error (NMSE), spectral efficiency (SE), and bit error rate (BER) across various velocities and signal-to-noise ratios. Ablation studies further confirm the effectiveness of each proposed module.

Population Risk Bounds for Kolmogorov-Arnold Networks Trained by DP-SGD with Correlated Noise

Authors: Puyu Wang, Jan Schuchardt, Nikita Kalinin, Junyu Zhou, Sophie Fellenz, Christoph Lampert, Marius Kloft

Abstract: We establish the first population risk bounds for Kolmogorov-Arnold Networks (KANs) trained by mini-batch SGD with gradient clipping, covering non-private SGD as well as differentially private SGD (DP-SGD) with Gaussian perturbations that interpolate between independent and temporally correlated noise. This setting is substantially closer to practice than prior KAN theory along two axes: training is by mini-batch SGD, the standard recipe for modern networks, rather than full-batch gradient descent (GD); and correlated-noise mechanisms have empirically shown a more favorable privacy-utility tradeoff than independent-noise mechanisms. Our results cover the corresponding full-batch GD and independent-noise DP-GD results for KANs by Wang et al. (2026), while yielding sharper fixed-second-layer specializations. The technical core is a new analysis route for correlated-noise DP training in the non-convex regime. Temporal dependence breaks the conditional-centering structure underlying standard one-step SGD arguments, and the projection step obstructs the exact cancellation structure of correlated perturbations. We address these difficulties through an auxiliary unprojected dynamics, a shifted iterate that absorbs the current noise perturbation, and a high-probability bootstrap certifying projection inactivity. Combining this optimization analysis with a stability-based generalization argument yields the stated population risk bounds. To the best of our knowledge, this is the first optimization and population risk analysis of a correlated-noise mechanism for DP training beyond convex learning, in particular for neural networks.

Wahkon: A Statistically Principled Deep RKHS Superposition Network

Authors: Yongkai Chen, Wenxuan Zhong, Ping Ma

Abstract: Deep learning excels at prediction but often lacks finite-sample guarantees and calibrated uncertainty; RKHS (Reproducing Kernel Hilbert Space)-based methods provide those guarantees but struggle to adapt in high dimensions. We propose Wahkon, a deep RKHS superposition network that unifies Kolmogorov’s superposition principle with RKHS regularization in the smoothing-spline tradition of Wahba. This yields a finite-dimensional deep representer theorem that makes training tractable and provides explicit layerwise complexity control. We show the penalized estimator is exactly the MAP (maximum a posteriori) estimate under a hierarchical Gaussian-process prior, extending the spline/GP duality to deep compositions. Using metric-entropy arguments, we establish minimax-optimal convergence rates under mild smoothness and clarify how depth and width trade off with regularity. Empirically, Wahkon outperforms multilayer perceptrons, Neural Tangent Kernels, and Kolmogorov–Arnold Networks across simulation benchmarks and a single-cell CITE-seq study. By unifying Kolmogorov’s superposition principle with RKHS regularization, Wahkon delivers accuracy, interpretability, and statistical rigor in a single framework.

Implicit spatial-frequency fusion of hyperspectral and lidar data via kolmogorov-arnold networks

Authors: Zekun Long, Judy X. Yang, Jing Wang, Ali Zia, Guanyiman Fu, Jun Zhou

Abstract: Hyperspectral image (HSI) classification is challenging in complex scenes due to spectral ambiguity, spatial heterogeneity, and the strong coupling between material properties and geometric structures. Although LiDAR provides complementary elevation information, most HSI-LiDAR fusion methods rely on CNNs or MLPs with fixed activation functions and linear weights. These methods struggle to model structural discontinuities in LiDAR data, intricate spectral features of HSI, and their interactions. In addition, fusion of the two modalities in both spatial and frequency domains with LiDAR guidance remains underexplored. To address these issues, we propose the Implicit Frequency-Geometry Fusion Network (IFGNet), which leverages Kolmogorov-Arnold Networks (KANs) with learnable spline-based functions to adaptively capture highly nonlinear relationships between hyperspectral and LiDAR features. Furthermore, IFGNet introduces a LiDAR-guided implicit aggregation module in both spatial and frequency domains, enhancing geometry-aware spatial representations while capturing global structural patterns. Experiments on the Houston 2013 and MUUFL benchmarks demonstrate that IFGNet consistently outperforms existing fusion methods in overall accuracy, average accuracy, and Cohen’s Kappa, while maintaining an efficient architecture.

This site is open source. Improve this page.